山东省济宁市任城区2021年中考数学一模试卷
试卷更新日期:2021-06-07 类型:中考模拟
一、单选题
-
1. 下列四个数中,2021的相反数是( )A、﹣2021 B、 C、﹣ D、20212. 下面计算正确的是( )A、(a3)3=a5 B、a3+a3=a6 C、a•a2=a3 D、a10÷a2=a53. 列四个图案中,不是轴对称图案的是( )A、
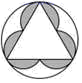 B、
B、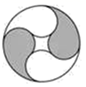 C、
C、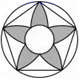 D、
D、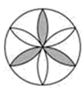 4. 用科学记数法表示202000为( )A、202×1000 B、2.02×105 C、2.02×104 D、(2.02)55. 某校为了解学生在校一周体育锻炼时间,随机调查了35名学生,调查结果列表如表,则这35名学生在校一周体育锻炼时间的中位数和众数分别为( )
4. 用科学记数法表示202000为( )A、202×1000 B、2.02×105 C、2.02×104 D、(2.02)55. 某校为了解学生在校一周体育锻炼时间,随机调查了35名学生,调查结果列表如表,则这35名学生在校一周体育锻炼时间的中位数和众数分别为( )锻炼时间/h
5
6
7
8
人数
6
15
10
4
A、6h,6h B、6h,15h C、6.5h,6h D、6.5h,15h6. 如图,△ABC的顶点均在⊙O上,若∠A=36°,则∠OBC的度数为( )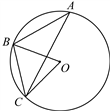 A、18° B、36° C、60° D、54°7. 如图,在△ABC中,AB=AC , BE⊥AC , D是AB的中点,且DE=BE , 则∠C的度数是( )
A、18° B、36° C、60° D、54°7. 如图,在△ABC中,AB=AC , BE⊥AC , D是AB的中点,且DE=BE , 则∠C的度数是( ) A、65° B、70° C、75° D、80°8. 某商务酒店客房有50间供客户居住.当每间房 每天定价为180元时,酒店会住满;当每间房每天的定价每增加10元时,就会空闲一间房.如果有客户居住,宾馆需对居住的每间房每天支出20元的费用.当房价定为多少元时,酒店当天的利润为10890元?设房价定为x元,根据题意,所列方程是( )A、 B、 C、 D、9. 如图①,直六棱柱的底面是正六边形,侧面ABCD中,AB=10cm,BC=20cm,现用一块矩形纸板EFGH制作图①中的直六棱柱,按图②中的方案裁剪,则GF的长是( )
A、65° B、70° C、75° D、80°8. 某商务酒店客房有50间供客户居住.当每间房 每天定价为180元时,酒店会住满;当每间房每天的定价每增加10元时,就会空闲一间房.如果有客户居住,宾馆需对居住的每间房每天支出20元的费用.当房价定为多少元时,酒店当天的利润为10890元?设房价定为x元,根据题意,所列方程是( )A、 B、 C、 D、9. 如图①,直六棱柱的底面是正六边形,侧面ABCD中,AB=10cm,BC=20cm,现用一块矩形纸板EFGH制作图①中的直六棱柱,按图②中的方案裁剪,则GF的长是( ) A、(20+10 )cm B、(30+10 )cm C、(20+20 )cm D、40 cm10. 如图,矩形ABCD中AB是3cm,BC是2cm,一个边长为1cm的小正方形沿着矩形ABCD的边AB→BC→CD→DA→AB连续地翻转,那么这个小正方形第一次回到起始位置时,小正方形箭头的方向是( )
A、(20+10 )cm B、(30+10 )cm C、(20+20 )cm D、40 cm10. 如图,矩形ABCD中AB是3cm,BC是2cm,一个边长为1cm的小正方形沿着矩形ABCD的边AB→BC→CD→DA→AB连续地翻转,那么这个小正方形第一次回到起始位置时,小正方形箭头的方向是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 因式分解:x2﹣x= .12. 如图,AD∥BE∥CF , AB=3,BC=6,DE=2,则EF的值为 .
 13. 如图,某轮船以每小时30海里的速度向正东方向航行,上午8:00,测得小岛C在轮船A的北偏东45°方向上;上午10:00,测得小岛C在轮船B的北偏西30°方向上,则轮船在航行中离小岛最近的距离约为海里(精确到1海里,参考数据 ≈1.414, ≈1.732).
13. 如图,某轮船以每小时30海里的速度向正东方向航行,上午8:00,测得小岛C在轮船A的北偏东45°方向上;上午10:00,测得小岛C在轮船B的北偏西30°方向上,则轮船在航行中离小岛最近的距离约为海里(精确到1海里,参考数据 ≈1.414, ≈1.732). 14. 抛物线y=ax2+bx+c的对称轴为直线x=﹣1,图象过(1,0)点,部分图象如图所示,下列判断:①abc>0;②b2﹣4ac>0;③5a﹣2b+c<0;④若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2 , 其中正确判断的序号是 .
14. 抛物线y=ax2+bx+c的对称轴为直线x=﹣1,图象过(1,0)点,部分图象如图所示,下列判断:①abc>0;②b2﹣4ac>0;③5a﹣2b+c<0;④若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2 , 其中正确判断的序号是 . 15. 将1, , , 按如图方式排列,若规定(m , n)表示第m排从左向右第n个数,则(6,3)与(2000,4)表示的两数之积是 .
15. 将1, , , 按如图方式排列,若规定(m , n)表示第m排从左向右第n个数,则(6,3)与(2000,4)表示的两数之积是 .
三、解答题
-
16. 先化简,再求值:(x﹣5)(x+1)+(x+2)2 , 其中x=﹣2.17. 某校组织八年级部分学生开展庆“五·四”演讲比赛,赛后对全体参赛学生成绩按A、B、C、D四个等级进行整理,得到下列不完整的统计图表.

等级
频数
频率
A
4
0.08
B
20
a
C
b
0.3
D
11
0.22
请根据所给信息,解答下列问题:
(1)、参加此次演讲比赛的学生共有人,a= , b= .(2)、请计算扇形统计图中B等级对应的扇形的圆心角的度数;(3)、已知A等级四名同学中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加县级比赛,请用列表法或树状图,求甲、乙两名同学都被选中的概率.18. 如图,直线y=ax+2与x轴交于点A(1,0),与y轴交于点B(0,b).将线段AB先向右平移1个单位长度,再向上平移t(t>0)个单位长度,得到对应线段CD , 反比例函数y= (x>0)的图象恰好经过C、D两点,连接AC、BD . (1)、请直接写出a和b的值;(2)、求反比例函数的表达式及四边形ABDC的面积.19. 甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天,且甲队单独施工45天和乙队单独施工30天的工作量相同.(1)、甲、乙两队单独完成此项任务各需多少天?(2)、设先由甲队施工x天,再由乙队施工y天,刚好完成筑路任务,求y与x之间的函数关系式.(3)、在 的条件下,若每天需付给甲队的筑路费用为0.1万元,需付给乙队的筑路费用为0.2万元,且甲、乙两队施工的总天数不超过24天,则如何安排甲、乙两队施工的天数,使施工费用最少,并求出最少费用.20. 如图,正方形ABCD和正方形AEFG有公共点A , 点B在线段DG上.
(1)、请直接写出a和b的值;(2)、求反比例函数的表达式及四边形ABDC的面积.19. 甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用10天,且甲队单独施工45天和乙队单独施工30天的工作量相同.(1)、甲、乙两队单独完成此项任务各需多少天?(2)、设先由甲队施工x天,再由乙队施工y天,刚好完成筑路任务,求y与x之间的函数关系式.(3)、在 的条件下,若每天需付给甲队的筑路费用为0.1万元,需付给乙队的筑路费用为0.2万元,且甲、乙两队施工的总天数不超过24天,则如何安排甲、乙两队施工的天数,使施工费用最少,并求出最少费用.20. 如图,正方形ABCD和正方形AEFG有公共点A , 点B在线段DG上.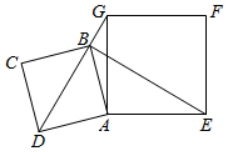 (1)、判断DG与BE的位置关系,并说明理由;(2)、若正方形ABCD的边长为1,正方形AEFG的边长为 ,求BE的长.21. 知识储备
(1)、判断DG与BE的位置关系,并说明理由;(2)、若正方形ABCD的边长为1,正方形AEFG的边长为 ,求BE的长.21. 知识储备在求二次函数y=ax2+bx+c(a>0)的最小值时,除了通过观察图象,还可以通过配方得到.把二次函数y=ax2+bx+c(a>0)的右边配方,得
y=ax2+bx+c
=a(x2+ x)+c
=a[x2+2• x+( )2﹣( )2]+c
=a(x+ )2+
∵a(x+ )2≥0,
∴当x=﹣ 时,二次函数y=ax2+bx+c(a>0)的最小值为 .
(1)、解决问题请你通过配方求函数y=x2+ 的最小值.
(2)、你能否通过配方求函数y=x+ (x>0)的最小值.(3)、数学模型已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
22. 如图,抛物线y=ax2﹣8x+c经过A(2,0),B(6,0)两点,直线l为抛物线的对称轴并与x轴交于点C . 直线y=﹣ x+2 与抛物线分别交于点B , D两点,与直线l交于点E . (1)、求抛物线的解析式;(2)、若以点A为圆心适当的长为半径画圆,使圆A与直线BD相切于点F , 求点F的坐标并说明直线l , y轴与圆A的位置关系.(3)、在(2)的条件下,在圆A上是否存在点G , 使得以G , O , C为顶点的三角形与△BCE相似.若存在,请直接写出G点坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、若以点A为圆心适当的长为半径画圆,使圆A与直线BD相切于点F , 求点F的坐标并说明直线l , y轴与圆A的位置关系.(3)、在(2)的条件下,在圆A上是否存在点G , 使得以G , O , C为顶点的三角形与△BCE相似.若存在,请直接写出G点坐标;若不存在,请说明理由.