山东省济宁市梁山县2021年中考数学一模试卷

试卷更新日期：2021-06-07 类型：中考模拟

进入出卷网下载

一、单选题

1. 已知a是 $- \frac{1}{2}$ ，则a的倒数为（）

A、2 B、 $\frac{1}{2}$ C、 $- \frac{1}{2}$ D、-2

查看试题解析
2. 若 $- 4 x^{m + 2} y^{4}$ 与 $2 x^{3} y^{n - 1}$ 为同类项，则m-n（）

A、-4 B、-3 C、-2 D、-1

查看试题解析
3. 围棋起源于中国，古代称之为“弈”，至今已有 $4000$ 多年的历史． $2017$ 年 $5$ 月，世界围棋冠军柯洁与人工智能机器人 $AlphaGo$ 进行围棋人机大战．截取首局对战棋谱中的四个部分，由黑白棋子摆成的图案是中心对称的是（）

A、 B、 C、 D、

查看试题解析
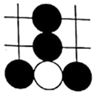4. 我国北斗公司在2020年发布了一款代表国内卫星导航系统最高水平的芯片，该芯片的制造工艺达到了0.000000022米.用科学记数法表示0.000000022为（）

A、22×10^﹣10 B、2.2×10^﹣10 C、2.2×10^﹣9 D、2.2×10^﹣8

查看试题解析
5. 下列几何体中，其左视图和俯视图相同的是（）

A、 B、 C、 D、

查看试题解析
6. 函数 $y = \sqrt{x - 2} + \sqrt{2 - x} + 2$ ，则 $x^{y}$ 的值为（）

A、0 B、2 C、4 D、8

查看试题解析
7. 在一个不透明的口袋中，装有a个红球和4个黄球，它们除颜色外没有任何区别，摇匀后从中随机摸出一个球，记下颜色后放回口袋中，摸到黄球的概率是0.2，则a的值是（）

A、16 B、20 C、25 D、30

查看试题解析
8. 一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形，边长都为1，则扇形和圆形纸板的面积比是（）

A、5：4 B、5：2 C、 $\sqrt{5}$ ：2 D、 $\sqrt{5}$ ： $\sqrt{2}$

查看试题解析
9.
如图，小王在长江边某瞭望台D处，测得江面上的渔船A的俯角为40°，若DE=3米，CE=2米，CE平行于江面AB，迎水坡BC的坡度i=1：0.75，坡长BC=10米，则此时AB的长约为（）（参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84）．

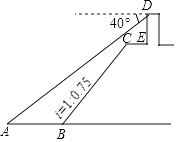A、5.1米 B、6.3米 C、7.1米 D、9.2米

查看试题解析
10.
下列图形都是由同样大小的菱形按照一定规律所组成的，其中第①个图形中一共有3个菱形，第②个图形中一共有7个菱形，第③个图形中一共有13个菱形，…，按此规律排列下去，第⑨个图形中菱形的个数为（）

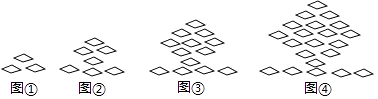A、73 B、81 C、91 D、109

查看试题解析

二、填空题

11. 《九章算术》中的算筹图是竖排的，为看图方便，我们把它改成横排，如图1、图2，图中各行从左到右列出的算筹数分别表示未知数 $x ， y$ 的系数与相应的常数项．把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来，就是 ${\begin{array}{l} 3 x + 2 y = 19 \\ x + 4 y = 23 \end{array} ．$ 类似地，图2所示的算筹图，可以表述为．

查看试题解析
12. 已知矩形ABCD的四个顶点均在反比例函数y= $\frac{1}{x}$ 的图象上，且点A的横坐标是2，则矩形ABCD的面积为．

查看试题解析
13. 因式分解： $3 m^{4} - 3 =$ ．

查看试题解析
14.
如图，在Rt△ABC中，∠BAC=90°，AB=15，AC=20，点D在边AC上，AD=5，DE⊥BC于点E，连结AE，则△ABE的面积等于．

查看试题解析
15. 如图，正方形 $A B C D$ 中， $A D = 4$ ，点E是对角线 $A C$ 上一点，连接 $D E$ ，过点E作 $E F ⊥ E D$ ，交 $A B$ 于点F ，连接 $D F$ ，交 $A C$ 于点G ，将 $△ E F G$ 沿 $E F$ 翻折，得到 $△ E F M$ ，连接 $D M$ ，交 $E F$ 于点N ，若点F是 $A B$ 边的中点，则 $△ E M N$ 的周长是．

查看试题解析

三、解答题

16. 先化简，再求值： $3 (x^{2} - x y) - 2 (x^{2} - y^{2}) + 3 x y$ ，其中 $x = - 2$ ， $y = 1$ ．

查看试题解析
17. 每年夏天全国各地总有未成年人因溺水而丧失生命，令人痛心疾首．今年某中学为确保学生安全，开展了“远离溺水，珍爱生命”的防溺水安全竞赛，学校对参加比赛的学生获奖情况进行了统计，绘制了如下两幅不完整的统计图，请结合图中相关数据解答下列问题．

(1)、求参加此安全竞赛的学生共有多少人；

(2)、在扇形统计图中，“三等奖”所对应的扇形的圆心角的度数为多少度？

(3)、求获得二等奖的人数，并将条形统计图补充完整．

查看试题解析
18. 某水果店第一次用600元购进水果若干千克，第二次又用600元购进该水果，但这次每千克的进价比第一次进价的提高了25%，购进数量比第一次少了30千克．

(1)、求第一次每千克水果的进价是多少元？

(2)、若要求这两次购进的水果按同一价格全部销售完毕后获利不低于420元，问每千克售价至少是多少元？

查看试题解析
19. 如图，AB是⊙O的一条弦，E是AB的中点，过点E作EC⊥OA于点C，过点B作⊙O的切线交CE的延长线于点D．

(1)、求证：DB=DE；

(2)、若AB=12，BD=5，求⊙O的半径．

查看试题解析
20. 综合与实践
背景阅读早在三千多年前，我国周朝数学家商高就提出：将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”．它被记载于我国古代著名数学著作《周髀算经》中，为了方便，在本题中，我们把三边的比为3：4：5的三角形称为（3，4，5）型三角形，例如：三边长分别为9，12，15或3 $\sqrt{2}$ ，4 $\sqrt{2}$ ，5 $\sqrt{2}$ 的三角形就是（3，4，5）型三角形，用矩形纸片按下面的操作方法可以折出这种类型的三角形．

实践操作如图1，在矩形纸片ABCD中，AD=8cm，AB=12cm．

第一步：如图2，将图1中的矩形纸片ABCD沿过点A的直线折叠，使点D落在AB上的点E处，折痕为AF，再沿EF折叠，然后把纸片展平．

第二步：如图3，将图2中的矩形纸片再次折叠，使点D与点F重合，折痕为GH，然后展平，隐去AF．

第三步：如图4，将图3中的矩形纸片沿AH折叠，得到△AD′H，再沿AD′折叠，折痕为AM，AM与折痕EF交于点N，然后展平．

(1)、问题解决
请在图2中证明四边形AEFD是正方形．

(2)、请在图4中判断NF与ND′的数量关系，并加以证明；

(3)、请在图4中证明△AEN（3，4，5）型三角形；

(4)、探索发现
在不添加字母的情况下，图4中还有哪些三角形是（3，4，5）型三角形？请找出并直接写出它们的名称．

查看试题解析
21. 阅读下列材料，并解答后面的问题．
在学习了直角三角形的边角关系后，小颖和小明两个学习小组继续探究任意锐角三角形的边角关系：在锐角△ABC中，∠A、∠B、∠C的对边分别是a、b、c ．

(1)、小明学习小组发现如下结论：
如图1，过A作AD⊥BC于D ，则sinB= $\frac{A D}{c}$ ，sinC= $\frac{A D}{b}$ 即AD=csinB ， AD=bsinC ，于是=即 $\frac{b}{\sin B} = \frac{c}{\sin C}$ ，同理有 $\frac{c}{\sin C} = \frac{a}{\sin A}$ ， $\frac{a}{\sin A} = \frac{b}{\sin B}$

则有 $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}$

(2)、小颖学习小组则利用圆的有关性质也得到了类似的结论：
如图2，△ABC的外接圆半径为R ，连结CO并延长交⊙O于点D ，连结DB ，则∠D=∠A ，

∵CD为⊙O的直径，∴∠DBC=90°，

在Rt△DBC中，

∵ $sinD = \frac{BC}{DC} = \frac{a}{2 R}$ ，

∴ $\sin A = \frac{a}{2 R}$ ， $\frac{a}{\sin A} = 2 R$

同理： $\frac{b}{\sin B} = 2 R ， \frac{c}{\sin C} = 2 R$ ，

则有 $\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2 R$

请你将这一结论用文字语言描述出来：．

小颖学习小组在证明过程中略去了“ $\frac{b}{\sin B} = 2 R ， \frac{c}{\sin C} = 2 R$ ”的证明过程，请你把“ $\frac{b}{\sin B} = 2 R ，$ ”的证明过程补写出来．

(3)、直接用前面阅读材料中得出的结论解决问题
规划局为了方便居民，计划在三个住宅小区A、B、C之间修建一座学校，使它到三个住宅小区的距离相等，已知小区C在小区B的正东方向 $\sqrt{3}$ 千米处，小区A在小区B的东北方向，且A与C之间相距 $\sqrt{2}$ 千米，求学校到三个小区的距离及小区A在小区C的什么方向？

查看试题解析
22. 如图1，在平面直角坐标系 $x O y$ 中，抛物线 $C ： y = a x^{2} + b x + c$ 与x轴相交于 $A ， B$ 两点，顶点为 $D (0 ， 4) ， A B = 4$ ，设点 $F (m ， 0)$ 是x轴的正半轴上一点，将抛物线C绕点F旋转 $180 °$ ，得到新的抛物线 $C^{'}$ ．

(1)、求抛物线C的函数表达式；

(2)、若抛物线 $C^{'}$ 与抛物线C在y轴的右侧有两个不同的公共点，求m的取值范围．

(3)、如图2，P是第一象限内抛物线C上一点，它到两坐标轴的距离相等，点P在抛物线 $C^{'}$ 上的对应点 $P^{'}$ ，设M是C上的动点，N是 $C^{'}$ 上的动点，试探究四边形 $P M P^{'} N$ 能否成为正方形？若能，求出m的值；若不能，请说明理由．

查看试题解析