山东省济南市章丘区2021年中考数学一模试卷
试卷更新日期:2021-06-07 类型:中考模拟
一、单选题
-
1. -3的相反数是( )A、-3 B、3 C、±3 D、2. 下列图形中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,由几个小正方体组成的立体图形的俯视图是( )
3. 如图,由几个小正方体组成的立体图形的俯视图是( )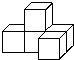 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列说法正确的有( )
4. 下列说法正确的有( )①绝对值等于本身的数是正数.②连接两点的线段的长度,叫做这两点的距离.③若 ,则点C就是线段 的中点.④不相交的两条直线是平行线.
A、1个 B、2个 C、3个 D、4个5. 为了更好地迎接庐阳区排球比赛,某校积极准备,从全校学生中遴选出21名同学进行相应的排球训练,该训练队成员的身高如下表:身高(cm)
170
172
175
178
180
182
185
人数(个)
2
4
5
2
4
3
1
则该校排球队21名同学身高的众数和中位数分别是(单位:cm)( )
A、185,178 B、178,175 C、175,178 D、175,1756. 实数 在数轴上的对应点的位置如图所示,下列关系式不成立的是( ) A、 B、 C、 D、7. 计算 ,结果正确的是( )A、 B、 C、 D、8. 如图所示,A、B点的坐标分别为(2,0),(0,1),且线段A1B1=AB,A1B1∥AB,若A1、B1点的坐表分别为(3,1),(a,b),则a+b的值为( )
A、 B、 C、 D、7. 计算 ,结果正确的是( )A、 B、 C、 D、8. 如图所示,A、B点的坐标分别为(2,0),(0,1),且线段A1B1=AB,A1B1∥AB,若A1、B1点的坐表分别为(3,1),(a,b),则a+b的值为( )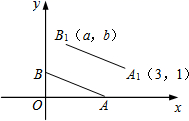 A、1 B、2 C、3 D、49. 如图,在矩形ABCD中,点E、F、G、H分别是边AD、AB、BC、CD的中点,连接EF、FG、GH . HE . 若AD=2AB , 则下列结论正确的是( )
A、1 B、2 C、3 D、49. 如图,在矩形ABCD中,点E、F、G、H分别是边AD、AB、BC、CD的中点,连接EF、FG、GH . HE . 若AD=2AB , 则下列结论正确的是( )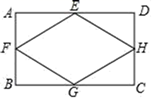 A、EF=AB B、 C、 D、10. 如图,在 中, , ,以点O为圆心 为半径作扇形 ,再以 为直径作半圆,则图中阴影部分的面积为( )
A、EF=AB B、 C、 D、10. 如图,在 中, , ,以点O为圆心 为半径作扇形 ,再以 为直径作半圆,则图中阴影部分的面积为( )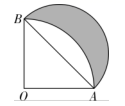 A、1 B、2 C、 D、11. 如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为10m,DE的长为5m,则树AB的高度是( )m.
A、1 B、2 C、 D、11. 如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为10m,DE的长为5m,则树AB的高度是( )m.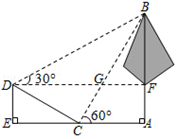 A、10 B、15 C、15 D、15 ﹣512. 已知二次函数 (其中 是自变量),当 时, 随 的增大而减小,且 时, 的最小值为15,则 的值为( )A、1或-2 B、 或 C、-2 D、1
A、10 B、15 C、15 D、15 ﹣512. 已知二次函数 (其中 是自变量),当 时, 随 的增大而减小,且 时, 的最小值为15,则 的值为( )A、1或-2 B、 或 C、-2 D、1二、填空题
-
13. 多项式 的公因式是 .14. 一个多边形的边数是10,则这个多边形的内角和是°.15. 如图,数轴上两点A , B , 在线段AB上任取一点C , 则点C到表示1的点的距离不大于2的概率是 .
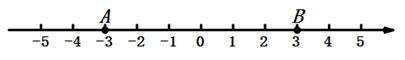 16. 对于平面坐标系中任意两点 、 定义一种新运算“*”为: ,根据这个规则,若 在第三象限, 在第四象限,则 在第象限.17. 学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地,两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示;根据图象信息知, 段的函数关系式是 .
16. 对于平面坐标系中任意两点 、 定义一种新运算“*”为: ,根据这个规则,若 在第三象限, 在第四象限,则 在第象限.17. 学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地,两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示;根据图象信息知, 段的函数关系式是 .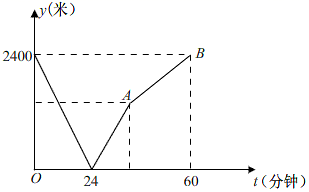 18. 如图,四边形ABCD是边长为m的正方形,若AF= m,E为AB上一点且BE=3,把△AEF沿着EF折叠,得到△A'EF,若△BA'E为直角三角形,则m的值为.
18. 如图,四边形ABCD是边长为m的正方形,若AF= m,E为AB上一点且BE=3,把△AEF沿着EF折叠,得到△A'EF,若△BA'E为直角三角形,则m的值为.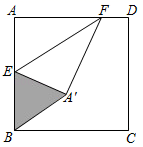
三、解答题
-
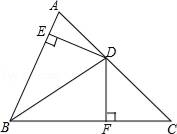
19. 计算:20. 解不等式组 ,并写出x的所有整数解.21. 如图,BD平分∠ABC交AC于点D,DE⊥AB于E,DF⊥BC于F,AB=6,BC=8,若S△ABC=28,求DE的长.
 22. 2020年疫情期间,某校为学生提供四种在线学习方式:在线阅读、在线听课、在线答疑、在线讨论,为了解学生的需求,对学生进行了“你最喜欢哪种在线学习方式的调查,调查结果制成两幅不完整统计图如图,根据图中信息回答问题:
22. 2020年疫情期间,某校为学生提供四种在线学习方式:在线阅读、在线听课、在线答疑、在线讨论,为了解学生的需求,对学生进行了“你最喜欢哪种在线学习方式的调查,调查结果制成两幅不完整统计图如图,根据图中信息回答问题: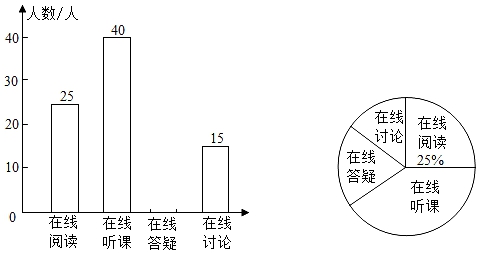 (1)、本次调查人数有人,在线答疑所在扇形的圆心角度数是;(2)、补全条形统计图;(3)、甲、乙两位同学都参加了在线学习,请用画树状图或列表的方法求出两名同学喜欢同一种在线学习方式的概率.23. 如图,已知 是 的直径, 是 的弦,点 在 外,连接 , 的平分线交 于点 .
(1)、本次调查人数有人,在线答疑所在扇形的圆心角度数是;(2)、补全条形统计图;(3)、甲、乙两位同学都参加了在线学习,请用画树状图或列表的方法求出两名同学喜欢同一种在线学习方式的概率.23. 如图,已知 是 的直径, 是 的弦,点 在 外,连接 , 的平分线交 于点 .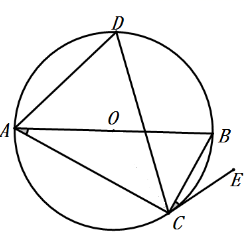 (1)、若 ,求证: 是 的切线;(2)、若 , ,求弦 的长.24. 大润发蔬菜超市从有机蔬菜批发市场批发蔬菜进行零售,部分蔬菜批发价格与零售价格如下表:
(1)、若 ,求证: 是 的切线;(2)、若 , ,求弦 的长.24. 大润发蔬菜超市从有机蔬菜批发市场批发蔬菜进行零售,部分蔬菜批发价格与零售价格如下表:蔬菜品种
西红柿
青椒
西兰花
豆角
批发价(元/ )
3.6
5.4
8
4.8
零售价(元/ )
5.4
8.4
14
7.6
请解答下列问题:
(1)、第一天,该超市批发西红柿和西兰花两种蔬菜共 ,用去了1520元钱,这两种蔬菜当天全部售完一共能赚多少元钱?(2)、第二天,该超市仍然批发西红柿和西兰花两种蔬菜共 ,且西红柿的数量不少于西兰花的1.5倍,怎样进货才能获得更大的利润,最大利润是多少?25. 如图,在平面直角坐标系中,菱形 的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数 的图象上,点D的坐标为 .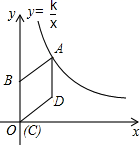 (1)、求k的值.(2)、若将菱形 沿x轴正方向平移m个单位,
(1)、求k的值.(2)、若将菱形 沿x轴正方向平移m个单位,①当菱形的顶点B落在反比例函数的图象上,求m的值;
②在平移中,若反比例函数图象与菱形的边 始终有交点,求m的取值范围.
26. 如图1,在 中, , , ,点D , E分别为 , 的中点. 绕点C顺时针旋转,设旋转角为 ( ,记直线 与直线 的交点为点P .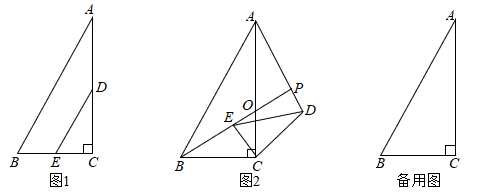 (1)、如图1,当 时, 与 的数量关系为 , 与 的位置关系为;(2)、当 时,上述结论是否成立?若成立,请仅就图2的情形进行证明;若不成立,请说明理由;(3)、 绕点C顺时针旋转一周,请直接写出运动过程中P点运动轨迹的长度和P点到直线 距离的最大值.27. 如图,抛物线 交x轴于 , 两点,与y轴交于点C , AC , BC . M为线段OB上的一个动点,过点M作 轴,交抛物线于点P , 交BC于点Q .
(1)、如图1,当 时, 与 的数量关系为 , 与 的位置关系为;(2)、当 时,上述结论是否成立?若成立,请仅就图2的情形进行证明;若不成立,请说明理由;(3)、 绕点C顺时针旋转一周,请直接写出运动过程中P点运动轨迹的长度和P点到直线 距离的最大值.27. 如图,抛物线 交x轴于 , 两点,与y轴交于点C , AC , BC . M为线段OB上的一个动点,过点M作 轴,交抛物线于点P , 交BC于点Q . (1)、求抛物线的表达式;(2)、过点P作 ,垂足为点N . 设M点的坐标为 ,请用含m的代数式表示线段PN的长,并求出当m为何值时PN有最大值,最大值是多少?(3)、试探究点M在运动过程中,是否存在这样的点Q , 使得以A , C , Q为顶点的三角形是等腰三角形.若存在,请求出此时点Q的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、过点P作 ,垂足为点N . 设M点的坐标为 ,请用含m的代数式表示线段PN的长,并求出当m为何值时PN有最大值,最大值是多少?(3)、试探究点M在运动过程中,是否存在这样的点Q , 使得以A , C , Q为顶点的三角形是等腰三角形.若存在,请求出此时点Q的坐标;若不存在,请说明理由.