山东省菏泽市巨野县2021年中考数学一模试卷
试卷更新日期:2021-06-07 类型:中考模拟
一、单选题
-
1. 要使式子 有意义,则m的取值范围是( )A、m>﹣1 B、m≥﹣1 C、m>﹣1且m≠1 D、m≥﹣1且m≠12. 在下列图形中,既是中心对称图形又是轴对称图形的是A、
 B、
B、 C、
C、 D、
D、 3. 下列四个多项式中,能因式分解的是( )A、a2+1 B、a2-6a+9 C、x2+5y D、x2-5y4. 一张桌子上摆放着若干个碟子,从三个方向上看在眼里,三种视图如下图所示,则这张桌子上共有碟子为( )
3. 下列四个多项式中,能因式分解的是( )A、a2+1 B、a2-6a+9 C、x2+5y D、x2-5y4. 一张桌子上摆放着若干个碟子,从三个方向上看在眼里,三种视图如下图所示,则这张桌子上共有碟子为( ) A、6个 B、8个 C、12个 D、17个5. 上体育课时,老师在运动场上教同学们学习掷铅球,训练时,李力同学掷出的铅球在场地上砸出了一个坑口直径约为10cm,深约为2cm的小坑,则该铅球的直径约为( )A、20cm B、19.5cm C、14.5cm D、10cm6. 如图所示,一个半径为r(r<1)的图形纸片在边长为10的正六边形内任意运动,则在该六边形内,这个圆形纸片不能接触到的部分面积是( )
A、6个 B、8个 C、12个 D、17个5. 上体育课时,老师在运动场上教同学们学习掷铅球,训练时,李力同学掷出的铅球在场地上砸出了一个坑口直径约为10cm,深约为2cm的小坑,则该铅球的直径约为( )A、20cm B、19.5cm C、14.5cm D、10cm6. 如图所示,一个半径为r(r<1)的图形纸片在边长为10的正六边形内任意运动,则在该六边形内,这个圆形纸片不能接触到的部分面积是( ) A、 B、 C、 D、7. 如图所示,正方形ABCD的边长为2,以对角线AC为一边作菱形AEFC , AF与BC交于G点,则∠BCE的度数与BE的长分别为( )
A、 B、 C、 D、7. 如图所示,正方形ABCD的边长为2,以对角线AC为一边作菱形AEFC , AF与BC交于G点,则∠BCE的度数与BE的长分别为( ) A、30°,2 -2 B、30°,2 -1 C、22.5°,2 -2 D、22.5°,2 -18. 如图, 中, , , ,点P是斜边AB上任意一点,过点P作 ,垂足为P,交边 或边 于点Q,设 , 的面积为y,则y与x之间的函数图象大致是
A、30°,2 -2 B、30°,2 -1 C、22.5°,2 -2 D、22.5°,2 -18. 如图, 中, , , ,点P是斜边AB上任意一点,过点P作 ,垂足为P,交边 或边 于点Q,设 , 的面积为y,则y与x之间的函数图象大致是 A、
A、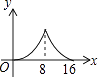 B、
B、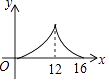 C、
C、 D、
D、
二、填空题
-
9. 2014年10月24日,“亚洲基础设施投资银行”在北京成立,我国出资500亿美元,这个数用科学记数法表示为 美元.
10. 若x+2y-3=0,则2x·4y的值为11. 如图所示,在⊙O中,直径MN=10,正方形ABCD的四个顶点分别在PM以及⊙O的半径OM,OP上,并且∠POM=45°,则AB的长为 . 12. 如图所示,有一圆柱形油罐,现要以油罐底部的一点A环绕油罐建梯子,并且要正好建到A点正上方的油罐顶部的B点,已知油罐高AB=5米,底面的周长是12米,则梯子最短长度为 .
12. 如图所示,有一圆柱形油罐,现要以油罐底部的一点A环绕油罐建梯子,并且要正好建到A点正上方的油罐顶部的B点,已知油罐高AB=5米,底面的周长是12米,则梯子最短长度为 . 13. 如图,点G是正方形ABCD的AB边的中点,点E、F在对角线AC上,并且AE=EF=FC,如果AB=2,则BF+GE= .
13. 如图,点G是正方形ABCD的AB边的中点,点E、F在对角线AC上,并且AE=EF=FC,如果AB=2,则BF+GE= . 14. 若直线y=m(m为常数)与函数y= 的图象恒有三个不同的交点,则常数m的取值范围是 .
14. 若直线y=m(m为常数)与函数y= 的图象恒有三个不同的交点,则常数m的取值范围是 .三、解答题
-
15. 计算:(π-2021)0-2sin45°+ + .16. 已知关于x , y的方程组 的解都为正数,求a的取值范围.17. 九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,求旗杆AB的高度.
 18. 列方程或方程组解应用题:
18. 列方程或方程组解应用题:小马自驾私家车从A地到B地,驾驶原来的燃油汽车所需油费108元,驾驶新购买的纯电动车所需电费27元,已知每行驶1千米,原来的燃油汽车所需的油费比新购买的纯电动汽车所需的电费多0.54元,求新购买的纯电动汽车每行驶1千米所需的电费.
19. 若关于x的一元二次方程x2﹣4x+k﹣3=0的两个实数根为x1、x2 , 且满足x1=3x2 , 试求出方程的两个实数根及k的值.20. 如图,已知反比例函数 的图象与一次函数 的图象相交于点A(1,4)和点B(n, ). (1)、求反比例函数和一次函数的解析式;(2)、当一次函数的值小于反比例函数的值时,直接写出x的取值范围.21. 如图,AB是⊙O的直径,AC是⊙O的弦,过点B作⊙O的切线DE,与AC的延长线交于点D,作AE⊥AC交DE于点E.
(1)、求反比例函数和一次函数的解析式;(2)、当一次函数的值小于反比例函数的值时,直接写出x的取值范围.21. 如图,AB是⊙O的直径,AC是⊙O的弦,过点B作⊙O的切线DE,与AC的延长线交于点D,作AE⊥AC交DE于点E. (1)、求证:∠BAD=∠E(2)、若⊙O的半径为5,AC=8,求BE的长.22. 2012年6月5日是“世界环境日”,南宁市某校举行了“绿色家园”演讲比赛,赛后整理参赛同学的成绩,制作成直方图(如图).
(1)、求证:∠BAD=∠E(2)、若⊙O的半径为5,AC=8,求BE的长.22. 2012年6月5日是“世界环境日”,南宁市某校举行了“绿色家园”演讲比赛,赛后整理参赛同学的成绩,制作成直方图(如图).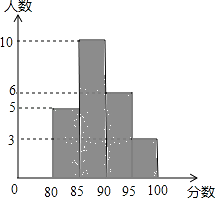 (1)、分数段在范围的人数最多;(2)、全校共有多少人参加比赛?(3)、学校决定选派本次比赛成绩最好的3人参加南宁市中学生环保演讲决赛,并为参赛选手准备了红、蓝、白颜色的上衣各1件和2条白色、1条蓝色的裤子.请用“列表法”或“树形图法”表示上衣和裤子搭配的所有可能出现的结果,并求出上衣和能搭配成同一种颜色的概率.23. 已知:如图所示,在四边形ABCD中,对角线的交点为O , E是OC上的一点,过点A作AG⊥BE于点G , AG , BD交于点F .
(1)、分数段在范围的人数最多;(2)、全校共有多少人参加比赛?(3)、学校决定选派本次比赛成绩最好的3人参加南宁市中学生环保演讲决赛,并为参赛选手准备了红、蓝、白颜色的上衣各1件和2条白色、1条蓝色的裤子.请用“列表法”或“树形图法”表示上衣和裤子搭配的所有可能出现的结果,并求出上衣和能搭配成同一种颜色的概率.23. 已知:如图所示,在四边形ABCD中,对角线的交点为O , E是OC上的一点,过点A作AG⊥BE于点G , AG , BD交于点F . (1)、如图①所示,若四边形ABCD是正方形,求证:OE=OF .(2)、如图②所示,若四边形ABCD是菱形,∠ABC=120°.探究线段OE与OF的数量关系,并说明理由.24. 如图,直线y=- x+2与x轴交于点B,与y轴交于点C,已知二次函数的图象经过点B,C和点A(-1,0).
(1)、如图①所示,若四边形ABCD是正方形,求证:OE=OF .(2)、如图②所示,若四边形ABCD是菱形,∠ABC=120°.探究线段OE与OF的数量关系,并说明理由.24. 如图,直线y=- x+2与x轴交于点B,与y轴交于点C,已知二次函数的图象经过点B,C和点A(-1,0).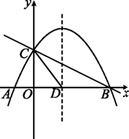 (1)、求B,C两点的坐标.(2)、求该二次函数的解析式.(3)、若抛物线的对称轴与x轴的交点为点D,则在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由.(4)、点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时点E的坐标.
(1)、求B,C两点的坐标.(2)、求该二次函数的解析式.(3)、若抛物线的对称轴与x轴的交点为点D,则在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由.(4)、点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时点E的坐标.