山东省东营市垦利区2021年中考数学一模试卷
试卷更新日期:2021-06-07 类型:中考模拟
一、单选题
-
1. 的平方根是( )
A、4 B、 C、2 D、2. 下列运算正确的是( )A、 B、 C、 D、﹣(﹣a+1)=a+13. 随着人们健康生活理念的提高,环保意识也不断增强,以下是回收、绿色包装、节水、低碳四个标志,其中是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 将一副三角板放在同一水平面上,如图摆放,使两个直角顶点重合,两条斜边平行,则∠1的度数是( )
4. 将一副三角板放在同一水平面上,如图摆放,使两个直角顶点重合,两条斜边平行,则∠1的度数是( ) A、45° B、60° C、75° D、85°5. 某射击运动员在训练中射击了10次,成绩如图所示:
A、45° B、60° C、75° D、85°5. 某射击运动员在训练中射击了10次,成绩如图所示: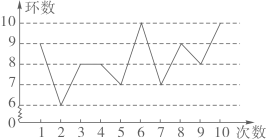
下列结论错误的是( )
A、众数是8 B、中位数是8 C、平均数是8.2 D、方差是1.26. 如图,要测量小河两岸相对的两点P,A的距离,可以在小河边取PA的垂线PB上的一点C,测得PC=100米,∠PCA=35°,则小河宽PA等于( )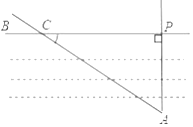 A、100sin35°米 B、100sin55°米 C、100tan35°米 D、100tan55°米7. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则正比例函数y=(b+c)x与反比例函数y= 在同一坐标系中的大致图象是( )
A、100sin35°米 B、100sin55°米 C、100tan35°米 D、100tan55°米7. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则正比例函数y=(b+c)x与反比例函数y= 在同一坐标系中的大致图象是( ) A、
A、 B、
B、 C、
C、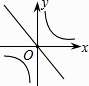 D、
D、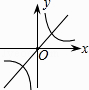 8. 《九章算术》中有这样一个题:今有甲乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?其意思为:今有甲乙二人,不如其钱包里有多少钱,若乙把其一半的钱给甲,则甲的数为50;而甲把其 的钱给乙,则乙的钱数也为50,问甲、乙各有多少钱?设甲的钱数为x,乙的钱数为y,则可建立方程组为( )A、 B、 C、 D、9. 如图1,E为矩形ABCD边AD上一点,点P从点B沿折线BE﹣ED﹣DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.若P,Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2).已知y与t的函数图象如图2,则下列结论错误的是( )
8. 《九章算术》中有这样一个题:今有甲乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?其意思为:今有甲乙二人,不如其钱包里有多少钱,若乙把其一半的钱给甲,则甲的数为50;而甲把其 的钱给乙,则乙的钱数也为50,问甲、乙各有多少钱?设甲的钱数为x,乙的钱数为y,则可建立方程组为( )A、 B、 C、 D、9. 如图1,E为矩形ABCD边AD上一点,点P从点B沿折线BE﹣ED﹣DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.若P,Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2).已知y与t的函数图象如图2,则下列结论错误的是( )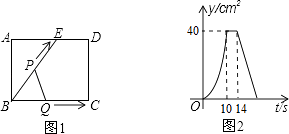 A、AE=6cm B、sin∠EBC= C、当0<t≤10时,y= t2 D、当t=12s时,△PBQ是等腰三角形10. 如图,在
A、AE=6cm B、sin∠EBC= C、当0<t≤10时,y= t2 D、当t=12s时,△PBQ是等腰三角形10. 如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( )。
ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( )。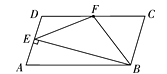 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 2020年是不平凡的一年,国家一手抓疫情防控,一手抓改革发展稳定,决战脱贫攻坚.“十三五”时期,脱贫攻坚成果举世瞩目,共有5575万农村贫困人口实现脱贫,5575万用科学记数法表示 .12. 因式分解: .13. 从 , , ,2,5中任取一数作为a的值,能使抛物线 的开口向下的概率为 .14. 如图,在△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连结CD.若CD=AC,∠A=48°,则∠ACB= .
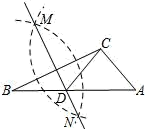 15. 已知关于x的分式方程 有一个正数解,则k的取值范围为.16. 自开展“全民健身运动”以来,喜欢户外步行健身的人越来越多.为方便群众步行健身,某地政府决定对一段如图1所示的坡路进行改造.如图2所示,改造前的斜坡 米,坡度为 ;将斜坡 的高度 降低 米后,斜坡 改造为斜坡 ,其坡度为 .则斜坡 的长为 . (结果保留根号)
15. 已知关于x的分式方程 有一个正数解,则k的取值范围为.16. 自开展“全民健身运动”以来,喜欢户外步行健身的人越来越多.为方便群众步行健身,某地政府决定对一段如图1所示的坡路进行改造.如图2所示,改造前的斜坡 米,坡度为 ;将斜坡 的高度 降低 米后,斜坡 改造为斜坡 ,其坡度为 .则斜坡 的长为 . (结果保留根号)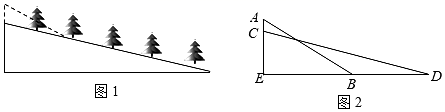 17. 如图, 的半径为2,圆心 的坐标为 ,点 是 上的任意一点, ,且 、 与 轴分别交于 、 两点,若点 、 关于原点 对称,则 的最小值为.
17. 如图, 的半径为2,圆心 的坐标为 ,点 是 上的任意一点, ,且 、 与 轴分别交于 、 两点,若点 、 关于原点 对称,则 的最小值为. 18. 如图所示,直线 ,点 坐标为 ,过点 作x轴的垂线交直线于点 ,以原点O为圆心, 长为半径画弧交x轴于点 ;再过点 作x轴的垂线交直线于点 ,以原点O为圆心, 长为半径画弧交x轴于点 ,…,按此做法进行下去,点 的坐标为 .
18. 如图所示,直线 ,点 坐标为 ,过点 作x轴的垂线交直线于点 ,以原点O为圆心, 长为半径画弧交x轴于点 ;再过点 作x轴的垂线交直线于点 ,以原点O为圆心, 长为半径画弧交x轴于点 ,…,按此做法进行下去,点 的坐标为 .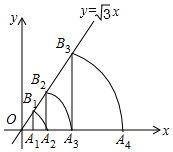
三、解答题
-
19.(1)、计算:(2)、先化简再求值: ,其中 .20. 2020年4月23日是第二十五个“世界读书日”.某校组织读书征文比赛活动,评选出一、二、三等奖若干名,并绘成如图所示的条形统计图和扇形统计图(不完整),请你根据图中信息解答下列问题:
 (1)、求本次比赛获奖的总人数,并补全条形统计图;(2)、求扇形统计图中“二等奖”所对应扇形的圆心角度数;(3)、获得一等奖的是2名男生和2名女生,学校从中随机抽取2人参加“世界读书日”宣传活动,请用列表法或画树状图的方法,求出恰好抽到1男1女的概率.21. 端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进 、 两种粽子1100个,购买 种粽子与购买 种粽子的费用相同,已知 粽子的单价是 种粽子单价的1.2倍.(1)、求 、 两种粽子的单价各是多少?(2)、若计划用不超过7000元的资金再次购买 、 两种粽子共2600个,已知 、 两种粽子的进价不变,求 中粽子最多能购进多少个?22. 如图,直线y1=﹣x+4,y2= x+b都与双曲线y= 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)、求本次比赛获奖的总人数,并补全条形统计图;(2)、求扇形统计图中“二等奖”所对应扇形的圆心角度数;(3)、获得一等奖的是2名男生和2名女生,学校从中随机抽取2人参加“世界读书日”宣传活动,请用列表法或画树状图的方法,求出恰好抽到1男1女的概率.21. 端午节是我国的传统节日,人们素有吃粽子的习俗,某商场在端午节来临之际用3000元购进 、 两种粽子1100个,购买 种粽子与购买 种粽子的费用相同,已知 粽子的单价是 种粽子单价的1.2倍.(1)、求 、 两种粽子的单价各是多少?(2)、若计划用不超过7000元的资金再次购买 、 两种粽子共2600个,已知 、 两种粽子的进价不变,求 中粽子最多能购进多少个?22. 如图,直线y1=﹣x+4,y2= x+b都与双曲线y= 交于点A(1,m),这两条直线分别与x轴交于B,C两点.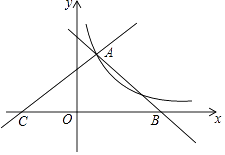 (1)、求y与x之间的函数关系式;
(1)、求y与x之间的函数关系式;
(2)、直接写出当x>0时,不等式 x+b> 的解集;(3)、若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.23. 已知如图, 为 的直径, 为 的弦, 垂直于过点 的直线 ,垂足为 ,且 平分 .
求证:
(1)、 是 的切线;(2)、 .24. 问题探究
 (1)、如图1,△ABC和△DEC均为等腰直角三角形,∠ACB=∠DCE=90°,点B , D , E在同一直线上,连接AD , BD .
(1)、如图1,△ABC和△DEC均为等腰直角三角形,∠ACB=∠DCE=90°,点B , D , E在同一直线上,连接AD , BD .①请探究AD与BD之间的位置关系:;
②若AC=BC= ,DC=CE= ,则线段AD的长为;
(2)、拓展延伸如图2,△ABC和△DEC均为直角三角形,∠ACB=∠DCE=90°,AC= ,BC= ,CD= ,CE=1.将△DCE绕点C在平面内顺时针旋转,设旋转角∠BCD为α(0°≤α<360°),作直线BD , 连接AD , 当点B , D , E在同一直线上时,画出图形,并求线段AD的长.
25. 如图,在平面直角坐标系中,点O为坐标原点,抛物线 的顶点是A(1,3),将OA绕点O顺时针旋转 后得到OB,点B恰好在抛物线上,OB与抛物线的对称轴交于点C. (1)、求抛物线的解析式;(2)、P是线段AC上一动点,且不与点A,C重合,过点P作平行于x轴的直线,与 的边分别交于M,N两点,将 以直线MN为对称轴翻折,得到 .
(1)、求抛物线的解析式;(2)、P是线段AC上一动点,且不与点A,C重合,过点P作平行于x轴的直线,与 的边分别交于M,N两点,将 以直线MN为对称轴翻折,得到 .设点P的纵坐标为m.
①当 在 内部时,求m的取值范围;
②是否存在点P,使 ,若存在,求出满足m的值;若不存在,请说明理由.