山东省德州市德城区2021年中考数学一模试卷

试卷更新日期：2021-06-07 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算|﹣2|^－1的结果是（）

A、2 B、 $- \frac{1}{2}$ C、－2 D、 $\frac{1}{2}$

查看试题解析
2. 下列各式计算正确的是（）

A、 ${(a - b)}^{2} = a^{2} - b^{2}$ B、 $a^{8} \div a^{4} = a^{2} (a \neq 0)$ C、 $2 a^{3} \cdot 3 a^{2} = 6 a^{5}$ D、 ${(- a^{2})}^{3} = a^{6}$

查看试题解析
3. 如图，AB∥CD ， ∠AEF＝52°，FG平分∠EFD ，则∠BGF的度数等于（）

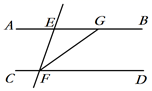A、154° B、152° C、136° D、144°

查看试题解析
4. 某几何体的三视图及相关数据(单位：cm)如图所示，则该几何体的侧面积是（）

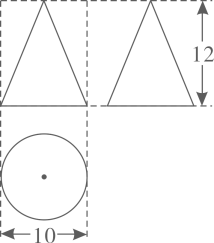A、 $\frac{65 π}{2} c m^{2}$ B、 $60 π c m^{2}$ C、 $65 π c m^{2}$ D、 $130 π c m^{2}$

查看试题解析
5. 在△ABC中，∠ACB＝90°，用直尺和圆规在AB上确定点D，使△ACD∽△CBD，根据作图痕迹判断，正确的是（　　）

A、 B、 C、 D、

查看试题解析
6. 不等式组 ${\begin{array}{l} 4 x - 3 > 2 x - 6 \\ \frac{2}{5} - x \geq - \frac{3}{5} \end{array}$ 的整数解有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 下表是某校合唱团成员的年龄分布：

年龄/岁

13

14

15

16

频数

5

15

$x$

$10 - x$

对于不同的 $x$ ，下列关于年龄的统计量不会发生改变的是（）

A、平均数､中位数 B、中位数､方差 C、平均数､方差 D、众数､中位数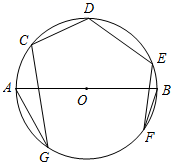

查看试题解析
8. 如图，点 $C 、 D 、 E 、 F 、 G$ 均在以 $A B$ 为直径的 $⊙ O$ 上，其中 $∠ A G C = 20^{°} ，$ $∠ B F E = 10^{°}$ ，则 $∠ C D E =$ （）

A、 $115^{°}$ B、 $120^{°}$ C、 $135^{°}$ D、 $150^{°}$

查看试题解析
9. 已知二次函数 y＝ax²＋bx＋c ，其中 y 与 x 的部分对应值如表：

x

-2

－1

0.5

1.5

y

5

0

－3.75

－3.75

下列结论正确的是（）

A、abc＜0 B、4a＋2b＋c＞0 C、若 x＜－1 或 x＞3 时，y＞0 D、方程 ax²＋bx＋c＝5 的解为 x₁＝－2，x₂＝3

查看试题解析
10. 对于实数 $a$ 、 $b$ ，定义一种新运算“ $\otimes$ ”为： $a \otimes b = \frac{1}{a - b^{2}}$ ，这里等式右边是实数运算．例如： $1 \otimes 3 = \frac{1}{1 - 3^{2}} = - \frac{1}{8}$ ．则方程 $x \otimes (- 2) = \frac{2}{x - 4} - 1$ 的解是（）

A、 $x = 4$ B、 $x = 5$ C、 $x = 6$ D、 $x = 7$

查看试题解析
11. 一条公路旁依次有 $A ， B ， C$ 三个村庄，甲乙两人骑自行车分别从 $A$ 村、 $B$ 村同时出发前往 $C$ 村，甲乙之间的距离 $s (k m)$ 与骑行时间 $t (h)$ 之间的函数关系如图所示，下列结论：① $A ， B$ 两村相距10 $k m$ ；②出发1.25 $h$ 后两人相遇；③甲每小时比乙多骑行8 $k m$ ；④相遇后，乙又骑行了15 $\min$ 或65 $\min$ 时两人相距2 $k m$ .其中正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
12. 如图，先有一张矩形纸片ABCD ， AB＝4，BC＝8，点M ， N分别在矩形的边AD ， BC上，将矩形纸片沿直线MN折叠，使点C落在矩形的边AD上，记为点P ，点D落在G处，连接PC ，交MN于点Q ，连接CM ．下列结论：①CQ＝CD；②四边形CMPN是菱形；③P ， A重合时，MN＝ $2 \sqrt{5}$ ；④△PQM的面积S的取值范围是4≤S≤5，其中正确的是（）

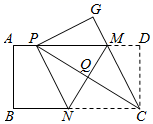A、①②④ B、②③④ C、①③ D、①②③④

查看试题解析

二、填空题

13. 计算： $3 \sqrt{9} - {(5 + π)}^{0} =$ ．

查看试题解析
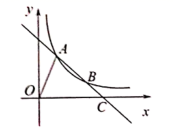
14. 在式子 $\frac{x - 2}{\sqrt{x + 1}}$ 中， $x$ 的取值范围是．

查看试题解析
15. 一个正多边形的内角和是外角和的3倍，则这个正多边形的一个内角的度数是度．

查看试题解析
16. 如图，直线AB交双曲线 $y = \frac{k}{x}$ 于A、B两点，交x轴于点C，且B恰为线段AC的中点，连结OA.若 $S_{△ O A C} = \frac{7}{2}$ ，则k的值为.

查看试题解析
17. 如图，在平面直角坐标系中，已知点O(0，0)，A(6，0)，B(0，8)，以某点为位似中心，作出△AOB的位似△CDE，则位似中心的坐标为.

查看试题解析
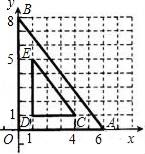18. 如图，在直角坐标系中，四边形ABCD是正方形，点A的坐标为（0，1），点B的坐标为（2，0）．点C的坐标为；若正方形ABCD和正方形A₁BC₁B₁关于点B成中心对称；正方形A₁BC₁B₁和正方形A₂B₂C₂B₁关于点B₁成中心对称；…，依此规律，则点C₆的坐标为．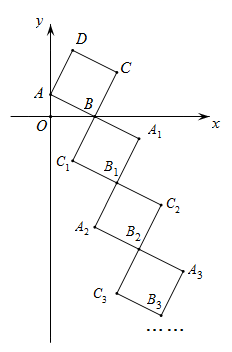

查看试题解析

三、解答题

19. 化简并求值 $(\frac{a - 2}{a^{2} + 2 a} - \frac{a - 1}{a^{2} + 4 a + 4}) \div \frac{a - 4}{a + 2}$ ，其中a满足 $a^{2} + 2 a - 1 = 0$

查看试题解析
20. “校园安全”越来越受到人们的关注，我市某中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题：

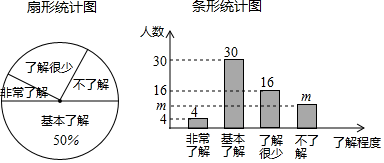(1)、接受问卷调查的学生共有人，条形统计图中m的值为；

(2)、扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为；

(3)、若该中学共有学生1800人，根据上述调查结果，可以估计出该学校学生中对校园安全知识达到“非常了解”和“基本了解”程度的总人数为人；

(4)、若从对校园安全知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加校园安全知识竞赛，请用列表或画树状图的方法，求恰好抽到1名男生和1名女生的概率.

查看试题解析
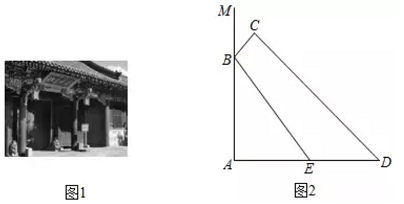21. 如图1，我国古建筑的大门上常常悬挂着巨大的匾额，图2中的线段 $B C$ 就是悬挂在墙壁AM上的某块匾额的截面示意图.已知 $B C = 2$ 米， $∠ M B C = 37 °$ .从水平地面点D处看点C，仰角 $∠ A D C = 45 °$ ，从点 $E$ 处看点 $B$ ，仰角 $∠ A E B = 53 °$ .且 $D E = 4.4$ 米，求匾额悬挂的高度 $A B$ 的长.（参考数据： $\sin 37 ° \approx \frac{3}{5}$ ， $\cos 37 ° \approx \frac{4}{5}$ ， $\tan 37 ° \approx \frac{3}{4}$ ）

查看试题解析
22. 某宝网店销售甲、乙两种电器，已知甲种电器每个的售价比乙种电器多60元，马老师从该网店购买了3个甲种电器和2个乙种电器，共花费780元．

(1)、该店甲、乙两种电器每个的售价各是多少元?

(2)、根据销售情况，店主决定用不少于10800元的资金购进甲、乙两种电器，这两种电器共100个，已知甲种电器每个的进价为150元，乙种电器每个的进价为80元．若所购进电器均可全部售出，请求出网店所获利润W(元)与甲种电器进货量m(个)之间的函数关系式，并说明当m为何值时所获利润最大?最大利润是多少?

查看试题解析
23. 如图，M，N是以AB为直径的⊙O上的点，且 $\overset{⌢}{A N}$ ＝ $\overset{⌢}{B N}$ ，弦MN交AB于点C，BM平分∠ABD，MF⊥BD于点F.

(1)、求证：MF是⊙O的切线；

(2)、若CN＝3，BN＝4，求CM的长.

查看试题解析
24. 请认真阅读下面的数学小探究系列，完成所提出的问题：

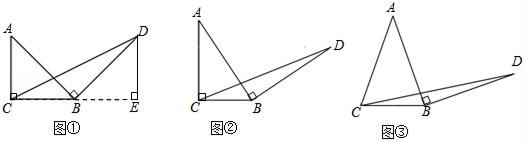(1)、探究1，如图①，在等腰直角三角形ABC中，∠ACB＝90°，BC＝3，将边AB绕点B顺时针旋转90°得到线段BD，连接CD，过点D做BC边上的高DE，则DE与BC的数量关系是， △BCD的面积为；

(2)、探究2，如图②，在一般的Rt△ABC中，∠ACB＝90°，BC＝a，将边AB绕点B顺时针旋转90°得到线段BD，连接CD，请用含a的式子表示△BCD的面积，并说明理由；

(3)、探究3：如图③，在等腰三角形ABC中，AB＝AC，BC＝a，将边AB绕点B顺时针旋转90°得到线段BD，连接CD，试探究用含a的式子表示△BCD的面积，要有探究过程．

查看试题解析
25. 如图1，抛物线y＝﹣x²＋bx＋c过点A（﹣1，0），点B（3，0）与y轴交于点C ．在x轴上有一动点E（m ， 0）（0 $<$ m $<$ 3），过点E作直线l⊥x轴，交抛物线于点M ．

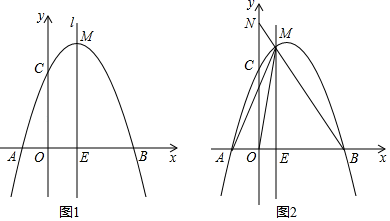(1)、求抛物线的解析式及C点坐标；

(2)、当m＝1时，D是直线l上的点且在第一象限内，若△ACD是以∠DCA为底角的等腰三角形，求点D的坐标；

(3)、如图2，连接BM并延长交y轴于点N ，连接AM ， OM ，设△AEM的面积为S₁ ， △MON的面积为S₂ ，若S₁＝2S₂ ，求m的值．

查看试题解析

年龄/岁	13	14	15	16
频数	5	15	$x$	$10 - x$

x	-2	－1	0.5	1.5
y	5	0	－3.75	－3.75