山东省滨州市无棣县2021年中考数学一模试卷
试卷更新日期:2021-06-07 类型:中考模拟
一、单选题
-
1. 的相反数为-2021,则 等于( )A、2021 B、-2021 C、 D、2. 自新型冠状病毒肺炎肆虐全球以来,万众一心战疫情已成为世界各国的共同语言,Worldometers世界实时统计数据显示,截至北京时间2021年3月25日7时01分,全球累计确诊新冠肺炎(COVID-19)病例超过125300000例,将125300000用科学记数法表示为( )A、1.253×107 B、1.253×108 C、0.1253×109 D、1253×1053. 四个运算:①a3+a2=a5;② ;③a6÷a3=a2;④(a﹣1)(a+2)=a2﹣2,运算结果正确的是( )A、① B、② C、③ D、④4. 如图,AB CD , AD⊥AC , ∠ACD=55°,则∠BAD=( )
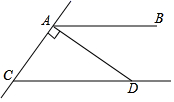 A、70° B、55° C、45° D、35°5. 为预防“新冠肺炎”,我县学校要求学生每日测量体温,九(1)班一名同学连续一周体温情况如表所示:则该名同学这一周体温数据的众数和中位数分别是( )
A、70° B、55° C、45° D、35°5. 为预防“新冠肺炎”,我县学校要求学生每日测量体温,九(1)班一名同学连续一周体温情况如表所示:则该名同学这一周体温数据的众数和中位数分别是( )日期
星期一
星期二
星期三
星期四
星期五
星期六
星期天
体温
36.3
36.3
36.6
36.4
36.3
36.5
36.4
A、36.4和36.3 B、36.3和36.4 C、36.3和36.3 D、36.3和36.26. 若关于 的一元二次方程 有实数根,则 的取值范围为( )A、 B、 且 C、 D、 且7. 疫情期间,小区的王阿姨和李奶奶通过外卖订购了两包蔬菜.王阿姨订购的一包蔬菜 包括西红柿、茄子、青椒各1千克,共花费11.8元;李奶奶订购的一包蔬菜包括西红柿2千克,茄子1.5千克,共花费13元,已知青椒每千克4.2元,则西红柿和茄子的价格是( )A、3.6元/千 克,4元千克 B、4.4 元/千克,3.2 元/千克 C、4元/千克,3.6元千克 D、3.2元/千克,4.4元/千克8. 如图,在平行四边形ABCD中,AE:DE=2:1,连接BE , 交AC于点F , AC=12,则AF为( )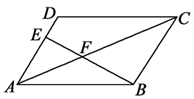 A、4 B、6 C、5.2 D、4.89. 如图,△ABC内接于⊙O , ∠A=60°.E是边BC的中点,连接OE并延长,交⊙O于点D , 连接BD , 则∠D的大小为( )
A、4 B、6 C、5.2 D、4.89. 如图,△ABC内接于⊙O , ∠A=60°.E是边BC的中点,连接OE并延长,交⊙O于点D , 连接BD , 则∠D的大小为( )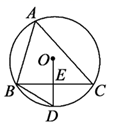 A、55° B、65° C、60° D、75°10. 生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a与全身b的高度比值接近0.618,可以增加视觉美感.若图中b为2米,则a约为( )
A、55° B、65° C、60° D、75°10. 生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a与全身b的高度比值接近0.618,可以增加视觉美感.若图中b为2米,则a约为( )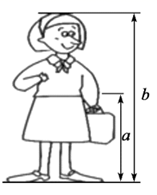 A、1.12米 B、1.24米 C、1.42米 D、1.62米11.
A、1.12米 B、1.24米 C、1.42米 D、1.62米11.如图,将等边△ABC绕点C顺时针旋转120°得到△EDC,连接AD,BD.则下列结论:
①AC=AD;②BD⊥AC;③四边形ACED是菱形.
其中正确的个数是( )
 A、0 B、1 C、2 D、312. 抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(﹣2,0),其部分图象如图所示,下列结论:①4ac<b2;②方程ax2+bx+c=0的两个根是x1=﹣2,x2=6;③a﹣b+c<0;④当y>0时,x的取值范围是﹣2≤x<2;⑤当x<0时y随x的增大而增大.其中正确结论的个数是( )
A、0 B、1 C、2 D、312. 抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(﹣2,0),其部分图象如图所示,下列结论:①4ac<b2;②方程ax2+bx+c=0的两个根是x1=﹣2,x2=6;③a﹣b+c<0;④当y>0时,x的取值范围是﹣2≤x<2;⑤当x<0时y随x的增大而增大.其中正确结论的个数是( )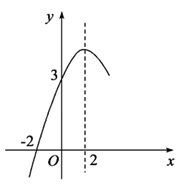 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
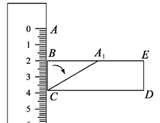
13. 若a+b=-4,a-b=2,则 = .14. 若一个多边形的内角和是900º,则这个多边形是边形.15. 分式 与 的和为2,则x的值为 .16. 如图所示,点A、B、C对应的刻度分别为0、2、4,将线段CA绕点C按顺时针方向旋转,当点A首次落在矩形BCDE的边BE上时,记为点A1 , 则此时线段CA扫过的图形的面积为 .
 17. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D , AB=8,AC=6,则cos∠DCB= .
17. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D , AB=8,AC=6,则cos∠DCB= .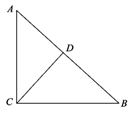 18. 数形结合是解决数学问题常用的思想方法.如图,直线y=x+5和直线y=ax+b相交于点P , 根据图象可知,方程x+5=ax+b的解是 .
18. 数形结合是解决数学问题常用的思想方法.如图,直线y=x+5和直线y=ax+b相交于点P , 根据图象可知,方程x+5=ax+b的解是 .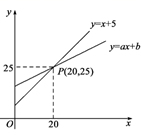 19. 如图,在矩形ABCD中,AB=4,BC=6,E是BC的中点,连接AE , P是边AD上一动点,沿过点P的直线将矩形折叠,使点D落在AE上的点D′处,当△APD′是直角三角形时,PD= .
19. 如图,在矩形ABCD中,AB=4,BC=6,E是BC的中点,连接AE , P是边AD上一动点,沿过点P的直线将矩形折叠,使点D落在AE上的点D′处,当△APD′是直角三角形时,PD= .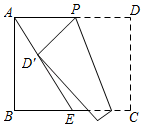 20. 观察下列各式: , , , ,…猜想: (n是正整数)= .
20. 观察下列各式: , , , ,…猜想: (n是正整数)= .三、解答题
-
21. 先化简再求值 ,其中x=(-2021)0+(﹣1)3+ ﹣ .22. 2021年1月,市教育局在全市中小学中选取了56所学校进行了教育满意度调查.评价小组在选取的某中学七年级全体学生中随机抽取了若干名学生家长进行了手机短信问卷调查,了解他们的孩子每天在课外用于学习的时间,并绘制成如下不完整的统计图.
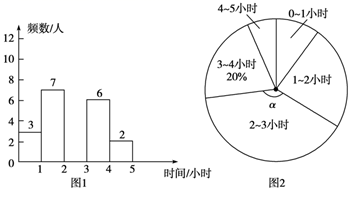
根据上述信息,解答下列问题:
(1)、本次抽取的学生家长人数是;扇形统计图中的圆心角α等于 .(2)、补全统计直方图.(3)、被抽取家长的孩子还要进行一次50米跑测试,每5人一组进行.在随机分组时,小红、小花两名女生被分到同一个小组,请用列表法或画树状图求出她俩在抽道次时抽在相邻两道的概率.(共五个道次)23. 如图,点 为正方形 对角线 上一点, 于点 , 于点 . (1)、求证: .(2)、若正方形 的边长为12,求,四边形 的周长.24. 如图所示,⊙O的半径为4,点A是⊙O上一点,直线l过点A;P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l于点B,交⊙O于点E,直径PD延长线交直线l于点F,点A是 的中点.
(1)、求证: .(2)、若正方形 的边长为12,求,四边形 的周长.24. 如图所示,⊙O的半径为4,点A是⊙O上一点,直线l过点A;P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l于点B,交⊙O于点E,直径PD延长线交直线l于点F,点A是 的中点.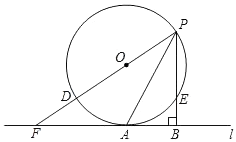 (1)、求证:直线l是⊙O的切线;(2)、若PA=6,求PB的长.
(1)、求证:直线l是⊙O的切线;(2)、若PA=6,求PB的长.
25. 如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,点E(4,n)在边AB上,反比例函数y= (k≠0)在第一象限内的图象经过点D、E,且D点的横坐标是它的纵坐标的2倍. (1)、求边AB的长;(2)、求反比例函数的解析式和n的值;(3)、若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.26. 如图,已知抛物线与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C(0,3).
(1)、求边AB的长;(2)、求反比例函数的解析式和n的值;(3)、若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折痕分别与x、y轴正半轴交于点H、G,求线段OG的长.26. 如图,已知抛物线与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C(0,3).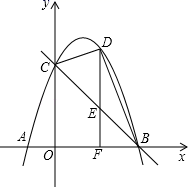 (1)、求抛物线的解析式;(2)、点D是第一象限内抛物线上的一个动点(与点C、B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连接BD、CD.设点D的横坐标为m,△BCD的面积为S.求S关于m的函数解析式及自变量m的取值范围,并求出S的最大值;(3)、已知M为抛物线对称轴上一动点,若△MBC是以BC为直角边的直角三角形,请直接写出点M的坐标.
(1)、求抛物线的解析式;(2)、点D是第一象限内抛物线上的一个动点(与点C、B不重合),过点D作DF⊥x轴于点F,交直线BC于点E,连接BD、CD.设点D的横坐标为m,△BCD的面积为S.求S关于m的函数解析式及自变量m的取值范围,并求出S的最大值;(3)、已知M为抛物线对称轴上一动点,若△MBC是以BC为直角边的直角三角形,请直接写出点M的坐标.