江苏省南京市2021年中考数学仿真模拟试卷(2)
试卷更新日期:2021-06-06 类型:中考模拟
一、单选题
-
1. 如图,M,N两点在数轴上表示的数分别是m,n,则下列式子中成立的是( )
 A、m+n<0 B、
A、m+n<0 B、 m<
m<  n
C、 |m|
n
C、 |m|  |n|>0
D、2+m<2+n
2.
|n|>0
D、2+m<2+n
2.如图,图1是由5个完全相同的正方体搭成的几何体,现将标有E的正方体平移至图2所示的位置,下列说法中正确的是( )
①左、右两个几何体的主视图相同
②左、右两个几何体的俯视图相同
③左、右两个几何体的左视图相同.
 A、①②③ B、②③ C、①② D、①③3. 下列判断中,你认为正确的是( )A、0的倒数是0 B、 是分数 C、 大于1 D、 的值是±24. 把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( )
A、①②③ B、②③ C、①② D、①③3. 下列判断中,你认为正确的是( )A、0的倒数是0 B、 是分数 C、 大于1 D、 的值是±24. 把图中的交通标志图案绕着它的中心旋转一定角度后与自身重合,则这个旋转角度至少为( ) A、30° B、90° C、120° D、180°5. 已知点O是 的外心,连接 并延长交 于D,若 ,则 的度数为( )
A、30° B、90° C、120° D、180°5. 已知点O是 的外心,连接 并延长交 于D,若 ,则 的度数为( ) A、 B、 C、 D、6. 如图,矩形ABCD中,AB=10,BC=5,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )
A、 B、 C、 D、6. 如图,矩形ABCD中,AB=10,BC=5,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为( )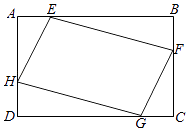 A、5 B、10 C、10 D、15
A、5 B、10 C、10 D、15二、填空题
-
7. 分解因式: =.
8. 不等式 的解集是 .9. 计算: .10. 若|b-1|+ =0,且一元二次方程kx2+ax+b=0有实数根,则k的取值范围是 .
11. 若计算 的结果为正整数,则无理数m的值可以是 . (写出一个符合条件的即可)12. 如图, 为 边 延长线上一点,过点 作 .若 , ,则 °.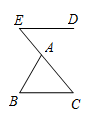 13. 如图,在四边形 中, .若将 沿 折叠,点 与边 的中点 恰好重合,则四边形 的周长为 .
13. 如图,在四边形 中, .若将 沿 折叠,点 与边 的中点 恰好重合,则四边形 的周长为 .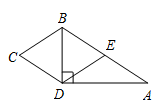 14. 如图,在△ABC中,AM:MD=4,BD:DC=2:3,则AE:EC= .
14. 如图,在△ABC中,AM:MD=4,BD:DC=2:3,则AE:EC= . 15. 如图矩形ABCD中,AB=1,AD= ,以AD的长为半径的⊙A交BC于点E,则图中阴影部分的面积为 .
15. 如图矩形ABCD中,AB=1,AD= ,以AD的长为半径的⊙A交BC于点E,则图中阴影部分的面积为 . 16. 已知点P的坐标为(m﹣1,m2﹣2m﹣3),则点P到直线y=﹣5的最小值为 .
16. 已知点P的坐标为(m﹣1,m2﹣2m﹣3),则点P到直线y=﹣5的最小值为 .三、解答题
-
17. 先化简,再求值: ,其中 .18. 如图,在△ABC中,DE∥AS,FG∥AC,BE=GC.求证:DE=FB.
 19. 图①,图②均为 的正方形网格,每个小正方形的顶点称为格点.在图①中已画出线段 ,在图②中已画出线段 ,其中 均为格点,按下列要求画图:
19. 图①,图②均为 的正方形网格,每个小正方形的顶点称为格点.在图①中已画出线段 ,在图②中已画出线段 ,其中 均为格点,按下列要求画图: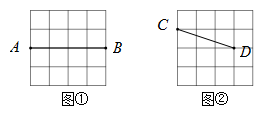 (1)、在图①中,以 为对角线画一个菱形 ,且 为格点;(2)、在图②中,以 为对角线画一个对边不相等的四边形 ,且 为格点, .20. 问题解决(1)、糖葫芦一般是用竹签串上山楂,再蘸以冰糖制作而成.现将一些山楂分别串在若干根竹签上.如果每根竹签串5个山楂,还剩余4个山楂;如果每根竹签串8个山楂,还剩余7根竹签.这些竹签有多少根?山楂有多少个?
(1)、在图①中,以 为对角线画一个菱形 ,且 为格点;(2)、在图②中,以 为对角线画一个对边不相等的四边形 ,且 为格点, .20. 问题解决(1)、糖葫芦一般是用竹签串上山楂,再蘸以冰糖制作而成.现将一些山楂分别串在若干根竹签上.如果每根竹签串5个山楂,还剩余4个山楂;如果每根竹签串8个山楂,还剩余7根竹签.这些竹签有多少根?山楂有多少个? (2)、反思归纳
(2)、反思归纳现有 根竹签, 个山楂.若每根竹签串 个山楂,还剩余 个山楂,则下列等式成立的是(填写序号).
⑴ ;⑵ ;⑶ .
21. 某中学为促进课堂教学,提高教学质量,对九年级学生进行了一次“你最喜欢的课堂教学方式”的问卷调查.根据收回的问卷,学校绘制了如下图表,请你根据图表中提供的信息,解答下列问题.编号
教学方式
最喜欢的频数
频率
1
教师讲,学生听
20
0.10
2
教师提出问题,学生探索思考
0.5
3
学生自行阅读教材,独立思考
30
4
分组讨论,解决问题
0.25
 (1)、请把三个图表中的空缺部分都补充完整;(2)、你最喜欢以上哪一种教学方式或另外的教学方式,请提出你的建议,并简要说明理由(字数在20字以内).22. 某公司举行一个游戏,规则如下:有4张背面相同的卡片,分别对应1000元、600元、400元、200元的奖金,现将4张纸牌洗匀后背面朝上摆放到桌上,让员工抽取,每人有两次抽奖机会,两次抽取的奖金之和作为公司发的奖金.现有两种抽取的方案:①小芳抽取方案是:直接从四张牌中抽取两张.②小明抽取的方案是:先从四张牌中抽取一张后放回去,再从四张中再抽取一张.你认为是小明抽到的奖金不少于1000元的概率大还是小芳抽取到的奖金少于1000元的概率大?请用树形图或列表法进行分析说明.23. 反比例函数y= (k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).
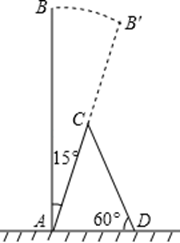
(1)、请把三个图表中的空缺部分都补充完整;(2)、你最喜欢以上哪一种教学方式或另外的教学方式,请提出你的建议,并简要说明理由(字数在20字以内).22. 某公司举行一个游戏,规则如下:有4张背面相同的卡片,分别对应1000元、600元、400元、200元的奖金,现将4张纸牌洗匀后背面朝上摆放到桌上,让员工抽取,每人有两次抽奖机会,两次抽取的奖金之和作为公司发的奖金.现有两种抽取的方案:①小芳抽取方案是:直接从四张牌中抽取两张.②小明抽取的方案是:先从四张牌中抽取一张后放回去,再从四张中再抽取一张.你认为是小明抽到的奖金不少于1000元的概率大还是小芳抽取到的奖金少于1000元的概率大?请用树形图或列表法进行分析说明.23. 反比例函数y= (k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).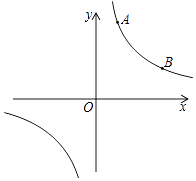 (1)、求反比例函数的解析式及B点的坐标;(2)、在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.24. 每年的6至8月份是台风多发季节,某次台风来袭时,一棵大树树干AB(假定树干AB垂直于地面)被刮倾斜15°后折断倒在地上,树的项部恰好接触到地面D(如图所示),量得树干的倾斜角为∠BAC=15°,大树被折断部分和地面所成的角∠ADC=60°,AD=4米,求这棵大树AB原来的高度是多少米?(结果精确
(1)、求反比例函数的解析式及B点的坐标;(2)、在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.24. 每年的6至8月份是台风多发季节,某次台风来袭时,一棵大树树干AB(假定树干AB垂直于地面)被刮倾斜15°后折断倒在地上,树的项部恰好接触到地面D(如图所示),量得树干的倾斜角为∠BAC=15°,大树被折断部分和地面所成的角∠ADC=60°,AD=4米,求这棵大树AB原来的高度是多少米?(结果精确到个位,参考数据: )
 25. 已知△ABC中,∠BCA=90°,BC=AC,D是BA边上一点(点D不与A,B重合),M是CA中点,当以CD为直径的⊙O与BA边交于点N,⊙O与射线NM交于点E,连接CE,DE.
25. 已知△ABC中,∠BCA=90°,BC=AC,D是BA边上一点(点D不与A,B重合),M是CA中点,当以CD为直径的⊙O与BA边交于点N,⊙O与射线NM交于点E,连接CE,DE. (1)、求证:BN=AN;(2)、猜想线段CD与DE的数量关系,并说明理由.26. 性质探究(1)、如图①,在等腰三角形 中, ,则底边 与腰 的长度之比为 .
(1)、求证:BN=AN;(2)、猜想线段CD与DE的数量关系,并说明理由.26. 性质探究(1)、如图①,在等腰三角形 中, ,则底边 与腰 的长度之比为 .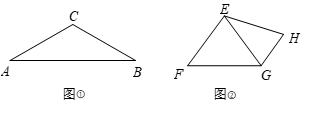 (2)、理解运用
(2)、理解运用若顶角为120°的等腰三角形的周长为 ,则它的面积为;
(3)、如图②,在四边形 中, .①求证: ;
②在边 上分别取中点 ,连接 .若 , ,直接写出线段 的长.
(4)、类比拓展顶角为 的等腰三角形的底边与一腰的长度之比为(用含 的式子表示).
27. 如图,抛物线 与x轴相交于 两点(点 在点 的左侧),与 轴相交于点 . 为抛物线上一点,横坐标为 ,且 .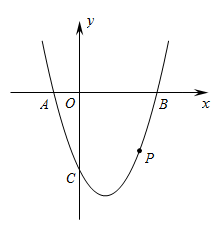 (1)、求此抛物线的解析式;(2)、当点 位于 轴下方时,求 面积的最大值;(3)、设此抛物线在点 与点 之间部分(含点 和点 )最高点与最低点的纵坐标之差为 .
(1)、求此抛物线的解析式;(2)、当点 位于 轴下方时,求 面积的最大值;(3)、设此抛物线在点 与点 之间部分(含点 和点 )最高点与最低点的纵坐标之差为 .①求 关于 的函数解析式,并写出自变量 的取值范围;
②当 时,直接写出 的面积.