苏科版2021年中考数学查漏补缺高分冲刺卷-解答题

试卷更新日期：2021-06-04 类型：三轮冲刺

进入出卷网下载

一、计算题

1.

(1)、计算： $- 2^{- 2} + | 1 - \frac{1}{\sin 45^{\circ}} | \times (\sqrt{8} + 2)$ ；

(2)、解方程： $\frac{x}{x - 1} - 1 = \frac{3}{x^{2} + x - 2}$ ．

查看试题解析
2. 计算题

(1)、计算：（ $\sqrt{15}$ -4）⁰+（ $\frac{1}{3}$ ）^-1-2cos30°- $|\sqrt{3} - 2|$ ；

(2)、解不等式组： $\{\begin{matrix} 3 (2 - x) \leq x + 5① \\ \frac{x + 10}{3} > 2 x② \end{matrix}$

查看试题解析
3. 化简下列各式：

(1)、（2a﹣1）²﹣4（a+1）（a﹣1）

(2)、 $(x + 1 - \frac{4 x - 5}{x - 1}) \div (\frac{1}{x} - \frac{1}{x^{2} - x})$

查看试题解析
4. （y–z）²+（x–y）²+（z–x）²=（y+z–2x）²+（z+x–2y）²+（x+y–2z）² ．求 $\frac{(y z + 1) (z x + 1) (x y + 1)}{(x^{2} + 1) (y^{2} + 1) (z^{2} + 1)}$ 的值．

查看试题解析
5.

(1)、已知a＜0，化简 $\sqrt{4 - {(a + \frac{1}{a})}^{2}}$ ﹣ $\sqrt{4 + {(a - \frac{1}{a})}^{2}}$

(2)、a+ $\frac{1}{a}$ =4（0＜a＜1），则 $\sqrt{a} - \frac{1}{\sqrt{a}}$ = ．

查看试题解析

二、解答题

6. 如图，线段AB的长为2，C为AB上一个动点，分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形 $△ A C D$ 和 $△ B C E$ ，求DE长的最小值．

查看试题解析
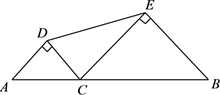7.
在平面直角坐标系xOy中，⊙C的半径为r，点P是与圆心C不重合的点，给出如下定义：若点P′为射线CP上一点，满足CP•CP′=r² ，则称点P′为点P关于⊙C的反演点．右图为点P及其关于⊙C的反演点P′的示意图．

（1）如图2，当⊙O的半径为1时，分别求出点M（1，0），N（0，2），T（ $\frac{1}{2}$ ， $\frac{1}{2}$ ）关于⊙O的反演点M′，N′，T′的坐标；

（2）如图3，已知点A（1，4），B（3，0），以AB为直径的⊙G与y轴交于点C，D（点C位于点D下方），E为CD的中点．

①若点O，E关于⊙G的反演点分别为O′，E′，求∠E′O′G的大小；

②若点P在⊙G上，且∠BAP=∠OBC，设直线AP与x轴的交点为Q，点Q关于⊙G的反演点为Q′，请直接写出线段GQ′的长度．

查看试题解析
8. 妈妈给小红和弟弟买了一本刘慈欣的小说《流浪地球》，姐弟俩都想先睹为快.是小红对弟弟说：我们利用下面中心涂黑的九宫格图案（如图所示）玩一个游戏，规则如下：我从第一行，你从第三行，同时各自任意选取一个方格，涂黑，如果得到的新图案是轴对称图形.我就先读，否则你先读.小红设计的游戏对弟弟是否公平？请用画树状图或列表的方法说明理由.（第一行的小方格从左至右分别用A，B，C表示，第三行的小方格从左至右分别用D，E，F表示）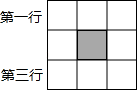

查看试题解析
9.
小昆和小明玩摸牌游戏，游戏规则如下：有3张背面完全相同，牌面标有数字1、2、3的纸牌，将纸牌洗匀后背面朝上放在桌面上，随机抽出一张，记下牌面数字，放回后洗匀再随机抽出一张。

（1）请用画树形图或列表的方法（只选其中一种），
表示出两次抽出的纸牌数字可能出现的所有结果；
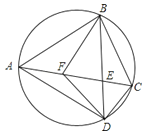
（2）若规定：两次抽出的纸牌数字之和为奇数，则小昆获胜；两次抽出的纸牌数字之和为偶数，则小明获胜。这个游戏公平吗？为什么？

查看试题解析
10. m是什么整数时，方程（m²﹣1）x²﹣6（3m﹣1）x+72＝0有两个不相等的正整数根．

查看试题解析
11.
如图，已知四边形ABCD内接于圆，对角线AC与BD相交于点E，F在AC上，AB=AD，∠BFC=∠BAD=2∠DFC．
（1）若∠DFC=40°，求∠CBF的度数；
（2）求证：CD⊥DF．

查看试题解析
12. 在一个阳光明媚的上午，数学陈老师组织学生测量小山坡的一颗大树CD的高度，山坡OM与地面ON的夹角为30°（∠MON=30°），站立在水平地面上身高1.7米的小明AB在地面的影长BP为1.2米，此刻大树CD在斜坡的影长DQ为5米，求大树的高度．

查看试题解析
13.
有一个几何体的形状为直三棱柱，右图是它的主视图和左视图．
（1）请补画出它的俯视图，并标出相关数据；
（2）根据图中所标的尺寸（单位：厘米），计算这个几何体的全面积．

查看试题解析
14. 如图，已知抛物线y= $- \frac{3}{4}$ x²+bx+c与坐标轴交于A，B，C三点，点A的横坐标为-1，过点C（0，3）的直线y= $- \frac{3}{4 t}$ x+3与x轴交于点Q，点P是线段BC上的一个动点，PH $⊥$ OB于点H．若PB=5t，且0<t<1．

（1）求b，c的值
（2）求出点B，Q，P的坐标（其中Q，P用含t的式子表示）：
（3）依点P的变化，是否存在t的值，使 $△$ PQB为等腰三角形？

查看试题解析
15. 如图，已知AB是⊙O的直径，BC是⊙O的切线，B为切点，OC平行于弦AD，连接CD。过点D作DE⊥AB于E，交AC于点P，求证：点P平分线段DE。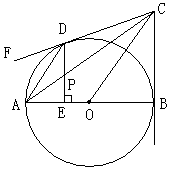

查看试题解析
16. 为从小明和小刚中选出一人去观看元旦文艺汇演，现设计了如下游戏，规则是：把四个完全相同的乒乓球标上数字1，2，3，4，然后放到一个不透明的袋中，一个人先从袋中随机摸出一个球，另一人再从剩下的三个球中随机摸出一个球．若摸出的两个球上的数字和为奇数，则小明去；否则小刚去．请用树状图或列表法说明这个游戏是否公平．

查看试题解析
17.
已知，二次函数 $y = a x^{2} + b x$ 的图像经过点A（-5，0）和点B，其中点B在第一象限，且OA=OB，cot∠BAO=2．

（1）求点B的坐标；
（2）求二次函数的解析式；
（3）过点B作直线BC平行于x轴，直线BC与二次函数图象的另一个交点为C，连结AC，如果点P在x轴上，且△ABC和△PAB相似，求点P的坐标．

查看试题解析
18.
在平面直角坐标系xOy中，抛物线y=mx²+(m+2)x+2过点(2，4)，且与x轴交于A、B两点（点A在点B左侧），与y轴交于点C.点D的坐标为(2，0)，连接CA，CB，CD.

（1）求证：∠ACO=∠BCD；
（2）p是第一象限内抛物线上的一个动点，连接DP交BC于点E.
①当△BDE是等腰三角形时，直接写出点E的坐标；
②连接CP，当△CDP的面积最大时，求点E的坐标.

查看试题解析
19.
如图1，抛物线y=ax²+bx+c（a≠0）与x轴交于点A（-1，0），B（4，0）两点，与y轴交于点C，且OC=3OA，点P是抛物线上的一个动点，过点P作PE⊥x轴于点E，交直线BC于点D，连接PC.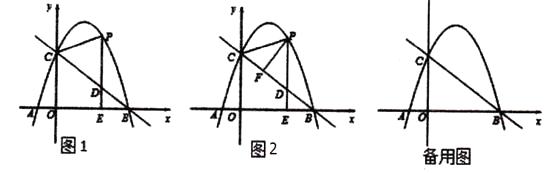

(1)、试求抛物线的解析式；

(2)、如图2，当动点P只在第一象限的抛物线上运动时，过点P作PF⊥BC于点F，试问△PFD的周长是否有最大值？如果有，请求出最大值；如果没有，请说明理由.

(3)、当点P在抛物线上运动时，将△CPD沿直线CP翻折，点D的对应点为点Q，试问，四边形CDPQ能否成为菱形?如果能，请求此时点P的坐标；如果不能，请说明理由.

查看试题解析
20.
如图，在Rt△ABC中，∠C=90°，顶点A、C的坐标分别为（﹣1，2），（3，2），点B在x轴上，点B的坐标为（3，0），抛物线y=﹣x²+bx+c经过A、C两点．
（1）求该抛物线所对应的函数关系式；
（2）点P是抛物线上的一点，当S_△_PAB= $\frac{5}{4}$ S_△_ABC时，求点P的坐标；
（3）若点N由点B出发，以每秒 $\frac{6}{5}$ 个单位的速度沿边BC、CA向点A移动， $\frac{1}{3}$ 秒后，点M也由点B出发，以每秒1个单位的速度沿线段BO向点O移动，当其中一个点到达终点时另一个点也停止移动，点N的移动时间为t秒，当MN⊥AB时，请直接写出t的值，不必写出解答过程．

查看试题解析
21.
已知：如图①，在平行四边形ABCD中，AB=12，BC=6，AD⊥BD．以AD为斜边在平行四边形ABCD的内部作Rt△AED，∠EAD=30°，∠AED=90°．

（1）求△AED的周长；
（2）若△AED以每秒2个单位长度的速度沿DC向右平行移动，得到△A₀E₀D₀ ，当A₀D₀与BC重合时停止移动，设运动时间为t秒，△A₀E₀D₀与△BDC重叠的面积为S，请直接写出S与t之间的函数关系式，并写出t的取值范围；
（3）如图②，在（2）中，当△AED停止移动后得到△BEC，将△BEC绕点C按顺时针方向旋转α（0°＜α＜180°），在旋转过程中，B的对应点为B₁ ， E的对应点为E₁ ，设直线B₁E₁与直线BE交于点P、与直线CB交于点Q．是否存在这样的α，使△BPQ为等腰三角形？若存在，求出α的度数；若不存在，请说明理由．

查看试题解析
22. 如图，在平面直角坐标系中，点A在x轴上，以OA为直径的半圆，圆心为B ，半径为1．过y轴上点C（0，2）作直线CD与⊙B相切于点E ，交x轴于点D ．二次函数y=ax²－2ax+c的图象过点C和D交x轴另一点为F点．

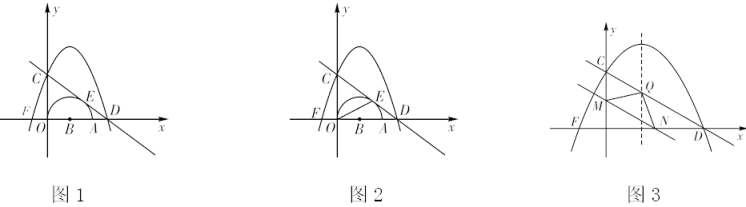(1)、求抛物线对应的函数表达式；

(2)、连接OE ，如图2，求sin∠AOE的值；

(3)、如图3，若直线CD与抛物线对称轴交于点Q ， M是线段OC上一动点，过M作MN//CD交x轴于N ，连接QM ， QN ，设CM=t ， △QMN的面积为S ，求S与t的函数关系式，并写出t的取值范围．S是否存在最大值，若存在，求出最大值；若不存在，说明理由．

查看试题解析
23. 如图，△ABC的边BC在直线l上，AD是△ABC的高，∠ABC=45°，BC=6cm，AB=2 $\sqrt{2}$ cm．点P从点B出发沿BC方向以1cm/s速度向点C运动，当点P到点C时，停止运动．PQ⊥BC，PQ交AB或AC于点Q，以PQ为一边向右侧作矩形PQRS，PS=2PQ．矩形PQRS与△ABC的重叠部分的面积为S（cm²），点P的运动时间为t（s）．回答下列问题：

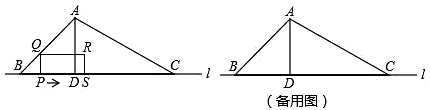(1)、AD=cm；

(2)、当点R在边AC上时，求t的值；

(3)、求S与t之间的函数关系式．

查看试题解析

三、作图题

24. 在生活中，有很多函数并不一定存在解析式，对于这样的函数，我们可以通过列表和图象来对它可能存在的性质进行探索，例如下面这样一个问题：

已知y是x的函数，下表是y与x的几组对应值．

x	…	﹣5	﹣4	﹣3	﹣2	0	1	2	3	4	5	…
y	…	1.969	1.938	1.875	1.75	1	0	﹣2	﹣1.5	0	2.5	…

小孙同学根据学习函数的经验，利用上述表格反映出的y与x之间的变化规律，对该函数的图象与性质进行了探究．

下面是小孙同学的探究过程，请补充完整；

(1)、如图，在平面之间坐标系xOy中，描出了以上表中各对应值为坐标的点，根据描出的点，画出函数的图象：

(2)、根据画出的函数图象回答：

①x＝﹣1时，对应的函数值y的为；

②若函数值y＞0，则x的取值范围是；

③写出该函数的一条性质（不能与前面已有的重复）：．

查看试题解析

25. 如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A(－2，1)，B(－1，4)，C(－3，2).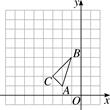

(1)、以原点O为位似中心，位似比为1∶2，在y轴的左侧，画出△ABC放大后的图形△A₁B₁C₁ ，并直接写出C₁点的坐标；

(2)、如果点D(a，b)在线段AB上，请直接写出经过(1)的变化后点D的对应点D₁的坐标.

查看试题解析
26. 如图，隧道的截面由抛物线和长方形构成．长方形的长为16m ，宽为6m ，抛物线的最高点C离路面AA₁的距离为8m ．

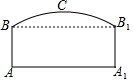(1)、建立适当的坐标系，求出表示抛物线的函数表达式；

(2)、一大型货车装载设备后高为7m ，宽为4m ．如果隧道内设双向行驶车道，那么这辆货车能否安全通过？

查看试题解析
27. 如图，图中的小方格都是边长为1的正方形，△ABC与△A′B′C′是关于点O为位似中心的位似图形，它们的顶点都在小正方形的格点上．

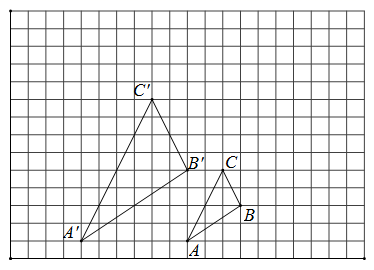(1)、画出位似中心O；

(2)、求出△ABC与△A′B′C′的相似比．

查看试题解析
28. 在10×6的网格中建立如图的平面直角坐标系，△ABC的顶点坐标分别为A（0，3），B（6，3），C（4，6）仅用无刻度的直尺在给定网格中按要求完成画图.

(1)、在CB上找点D，使AD平分∠BAC；

(2)、在AB上找点F，使∠CFA＝∠DFB；

(3)、在BC上找点M、N，使BM＝MN＝NC.[（1）（2）画在图1中，（3）画在图2中].

查看试题解析
29. 【问题提出】如何把n个边长为1的正方形，剪拼成一个大正方形？

(1)、【解决方法】探究一：若n是完全平方数，我们不用剪切小正方形，可直接将小正方形拼成一个大正方形，如图(1)，用四个边长为1的小正方形可以拼成一个大正方形.
问题1：请用9个边长为1的小正方形在图(2)的位置拼成一个大正方形.

(2)、【解决方法】探究二：若n＝2，5，10，13等这些数，都可以用两个正整数的平方和来表示，以n＝5为例，用5个边长为1的小正方形剪拼成一个大正方形.
计算：拼成的大正方形的面积为5，边长为 $\sqrt{5}$ ，可表示成 $\sqrt{2^{2} + 1^{2}}$ ；

剪切：如图(3)将5个小正方形按如图所示分成5部分，虚线为剪切线；

拼图：以图(3)中的虚线为边，拼成一个边长为 $\sqrt{5}$ 的大正方形，如图(4).

问题2：请仿照上面的研究方式，用13个边长为1的小正方形剪拼成一个大正方形；

①计算：拼成的大正方形的面积为，边长为，可表示成；

②剪切：请仿照图(3)的方法，在图(5)的位置画出图形.

③拼图：请仿照图(4)的方法，在图(6)的位置出拼成的图.

查看试题解析

四、综合题

30. 如图，已知一次函数y₁= $\frac{4}{3}$ x﹣4与反比例函数y₂= $\frac{k}{x}$ 的图象在第一象限相交于点A（6，n），与x轴相交于点B．

(1)、填空：n的值为， k的值为；当y2≥﹣4时，x的取值范围是；

(2)、以AB为边作菱形ABCD，使点C在点B右侧的x轴上，求点D的坐标．

查看试题解析

31.

(1)、完成下列表格，并回答下列问题，

锐角 $α$	$30 °$	$45 °$	$60 °$
$\sin α$
$\cos α$
$\tan α$

(2)、当锐角

α

逐渐增大时，

\sin α

的值逐渐，

\cos α

的值逐渐，

\tan α

的值逐渐．

(3)、

\sin 30 ° = \cos

，

\sin

= \cos 60 °

；

(4)、

\sin^{2} 30 ° + \cos^{2} 30 ° =

；

(5)、

\frac{\sin 30 °}{\cos 30 °} = \tan

；

(6)、若

\sin α = \cos α

，则锐角

α =

．

查看试题解析

32. 如图，已知圆内接四边形 $A B D C$ 中， $∠ B A C = 60^{\circ}$ ， $A B = A C$ ， $A D$ 为它的对角线.

(1)、求 $∠ A D B$ 与 $∠ A D C$ 的大小；

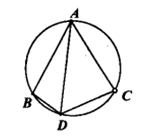(2)、求证： $A D = B D + C D$ .

查看试题解析
33. 如图，Rt△ABC中，∠ABC=90°，以AB为直径的⊙O交AC于点D，E是BC的中点，连接DE、OE．

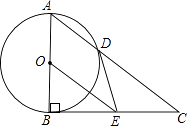(1)、求证：DE与⊙O相切；

(2)、求证：BC²=2CD•OE；

(3)、若cosC= $\frac{2}{3}$ ，DE=4，求AD的长．

查看试题解析
34. 如图1，抛物线 $y = \frac{1}{3} x^{2} + b x + c$ 过点 $A (4 ， - 1)$ ， $B (0 ， - \frac{11}{3})$ ，点 $C$ 为直线 $A B$ 下方抛物线上一动点， $M$ 为抛物线顶点，抛物线对称轴与直线 $A B$ 交于点 $N$ .

(1)、求抛物线的表达式与顶点 $M$ 的坐标；

(2)、在直线 $A B$ 上是否存在点 $D$ ，使得 $C$ ， $D$ ， $M$ ， $N$ 为顶点的四边形是平行四边形，若存在，请求出 $D$ 点坐标；

(3)、在 $y$ 轴上是否存在点 $Q$ ，使 $∠ A Q M = 45 °$ ？若存在，求点 $Q$ 的坐标；若不存在，请说明理由.

查看试题解析
35. 在平面直角坐标系中，二次函数 $y = a x^{2} + b x + 2$ 的图象与 $x$ 轴交于A（－3，0），B（1，0）两点，与y轴交于点C．

(1)、求这个二次函数的解析式；

(2)、点P是直线AC上方的抛物线上一动点，是否存在点P，使△ACP的面积最大？若存在，求出点P的坐标；若不存在，说明理由；

(3)、点Q是直线AC上方的抛物线上一动点，过点Q作QE垂直于 $x$ 轴，垂足为E．是否存在点Q，使以点B、Q、E为顶点的三角形与△AOC相似？若存在，直接写出点Q的坐标；若不存在，说明理由；

查看试题解析