浙江省宁波市鄞州区2020-2021学年七年级下学期数学期中考试试卷

试卷更新日期：2021-06-04 类型：期中考试

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 下列等式中成立的是（）

A、 $a^{4} \cdot a = a^{4}$ B、 $a^{6} \div a^{3} = a^{2}$ C、 ${(a^{3})}^{2} = a^{5}$ D、 ${(a b^{2})}^{3} = a^{3} b^{6}$

查看试题解析
2. 下列从左到右的变形属于因式分解的是（）

A、 $(x + 1) (x - 1) = x^{2} - 1$ B、 $m^{2} - 2 m - 3 = m (m - 2) - 3$ C、 $2 x^{2} + 1 = x (2 x + \frac{1}{x})$ D、 $x^{2} - 5 x + 6 = (x - 2) (x - 3)$

查看试题解析
3. 据了解，新型冠状病毒（SARS﹣CoV﹣2）的最大直径大约是0.00000014米.数0.00000014用科学记数法表示为（）

A、1.4×10^﹣⁵ B、1.4×10^﹣⁶ C、1.4×10^﹣⁷ D、14×10^﹣⁷

查看试题解析
4. 如图，将一直角三角板与两边平行的纸条如图所示放置，下列结论：

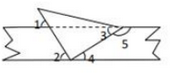
（1）∠1＝∠2；（2）∠3＝∠4；（3）∠2+∠4＝90°；（4）∠4+∠5＝180°，
其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
5. 若方程组 ${\begin{cases} x + y = ★ \\ 2 x + y = 16 \end{cases}$ 的解为 ${\begin{cases} x = 6 \\ y = ■ \end{cases}$ ，那么被“★”、“■”遮住的两数分别是（）

A、10，4 B、4，10 C、3，10 D、10，3

查看试题解析
6. 一副三角板按如图方式摆放，且∠1比∠2大50°.若设∠1＝ $x$ °，∠2＝ $y$ °，则可得到的方程组为（）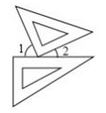

A、 ${\begin{cases} x = y - 50 \\ x + y = 180 \end{cases}$ B、 ${\begin{cases} x = y + 50 \\ x + y = 180 \end{cases}$ C、 ${\begin{cases} x = y - 50 \\ x + y = 90 \end{cases}$ D、 ${\begin{cases} x = y + 50 \\ x + y = 90 \end{cases}$

查看试题解析
7.
如图，已知AB∥DE，∠ABC＝70°，∠CDE＝140°，则∠BCD的值为（）

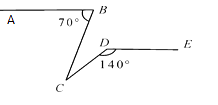A、70° B、50° C、40° D、30°

查看试题解析
8. 从图1到图2的变化过程可以发现的代数结论是（）

A、（a+b）（a﹣b）＝a²﹣b² B、a²﹣b²＝（a+b）（a﹣b） C、（a+b）²＝a²+2ab+b² D、a²+2ab+b²＝（a+b）²

查看试题解析
9. 方程 $(m^{2} - 9) x^{2} + x - (m - 3) y = 0$ 是关于， $y$ 的二元一次方程，则 $m$ 的值为（）

A、±3 B、3 C、-3 D、9

查看试题解析
10. 有下列说法：
①在同一平面内，过直线外一点有且只有一条直线与已知直线平行；②无论k取任何实数，多项式x²﹣ky²总能分解成两个一次因式积的形式；③若（t﹣3）³^﹣^2t＝1，则t可以取的值有3个；④关于x，y的方程组为 ${\begin{matrix} a x + 2 y = - 5 \\ - x + a y = 2 a \end{matrix}$ ，将此方程组的两个方程左右两边分别对应相加，得到一个新的方程，当a每取一个值时，就有一个确定的方程，而这些方程总有一个公共解，则这个公共解是 ${\begin{matrix} x = 3 \\ y = - 1 \end{matrix}$ .

其中正确的说法是（）

A、①④ B、①③④ C、②③ D、①③

查看试题解析

二、填空题（每小题3分，共18分）

11. 因式分解：a²﹣2a= ．

查看试题解析
12. （﹣2021）⁰+（ $\frac{1}{2}$ ）^﹣²+（﹣3）³=

查看试题解析
13. 如图，在△ABC中，BC＝10cm，D是BC的中点，将△ABC沿BC向右平移得△A′DC′，则点A平移的距离AA′＝cm.

查看试题解析
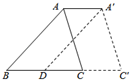14. 如图，下列条件中：①∠BAD+∠ABC＝180°；②∠1＝∠2；③∠3＝∠4；④∠BAD＝∠BCD，能判定AD∥BC的是.

查看试题解析
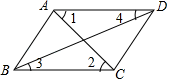15. 若4x²+（a﹣1）xy+9y²是完全平方式，则a的值是

查看试题解析
16. 如图，直线 $l_{1}$ ⊥直线 $l_{2}$ ，垂足为O，Rt△ABC如图放置，过点B作BD∥AC交直线 $l_{2}$ 于点D，在△ABC内取一点E，连接AE，DE.

(1)、若∠CAE＝15°，∠EDB＝25°，则∠AED＝ °.

(2)、若∠EAC＝ $\frac{1}{n}$ ∠CAB，∠EDB＝ $\frac{1}{n}$ ∠ODB，则∠AED＝°.（用含n的代数式表示）

查看试题解析

三、解答题（有7题，共52分）

17.

(1)、解方程：① ${\begin{matrix} y = 2 x - 1 \\ x + 2 y = - 7 \end{matrix}$ ② ${\begin{matrix} 2 m + 3 n = 1 \\ 7 m + 6 n = 2 \end{matrix}$ .

(2)、简便计算：19.9²+19.9×0.2+0.1².

查看试题解析
18. 先化简，再求值： $(2 x + 3) (2 x - 3) + {(x - 2)}^{2} - 4 x (x - 1)$ ，其中 x=2 .

查看试题解析
19.
如图：在正方形网格中有一个△ABC，按要求进行下列作图（只借助于网格，需写出结论）：

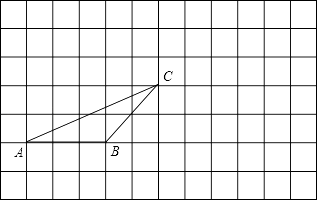(1)、过点A画出BC的平行线；

(2)、画出先将△ABC向右平移5格，再向上平移3格后的△DEF；

查看试题解析
20.

(1)、已知a+b＝5，ab＝ $- \frac{1}{4}$ ，求下列各式的值：
①a²+b²； ②（a﹣b）².

(2)、若2x+3y﹣4z+1＝0，求9^x•27^y÷81^z的值.

查看试题解析
21. 如图，已知 $∠ A = ∠ C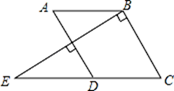$ ， $A D ⊥ B E$ ， $B C ⊥ B E$ ，点 $E$ ， $D$ ， $C$ 在同一条直线上.

(1)、判断 $A B$ 与 $C D$ 的位置关系，并说明理由.

(2)、若 $∠ A B C = 120 °$ ，求 $∠ B E C$ 的度数.

查看试题解析

22. 某电器超市销售每台进价为80元、200元的A，B两种型号的电风扇，如表所示是六月份前2周的销售情况：（进价、售价均保持不变，利润＝销售收入﹣进货成本）

销售时段	销售数量		销售收入
销售时段	A种型号	B种型号	销售收入
第一周	6	5	2100元
第二周	4	10	3400元

(1)、求A、B两种型号的电风扇的销售单价.

(2)、若超市一共采购这两种型号的电风扇共120台，售完后该超市能否实现利润刚好达到8000元？若能，请给出相应的采购方案；若不能，请说明理由.

查看试题解析

23. 我们通常用作差法比较代数式大小.例如：已知M＝2x+3，N＝2x+1，比较M和N的大小.先求M﹣N，若M﹣N＞0，则M＞N；若M﹣N＜0，则M＜N；若M﹣N＝0，则M＝N，反之亦成立.本题中因为M-N＝（2x+3）-（2x+1）＝2＞0，所以M＞N.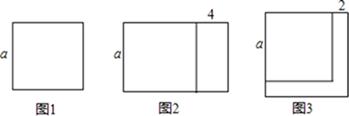

(1)、如图1是边长为a的正方形，将正方形一边不变，另一边增加4，得到如图2所示的新长方形，此长方形的面积为S₁；将图1中正方形边长增加2得到如图3所示的新正方形，此正方形的面积为S₂.用含a的代数式表示S₁＝， S₂＝（需要化简）.然后请用作差法比较S₁与S₂大小；

(2)、已知A＝2a²﹣6a+1，B＝a²﹣4a﹣1，请你用作差法比较A与B大小.

(3)、若M＝（a﹣4）² ， N＝16﹣（a﹣6）² ，且M＝N，求（a﹣4）（a﹣6）的值.

查看试题解析