广东省深圳市大鹏新区2021年中考数学一模试卷

试卷更新日期：2021-06-04 类型：中考模拟

进入出卷网下载

一、选择题

1. 2020的相反数是（　　）

A、2020 B、±2020 C、﹣2020 D、 $\frac{1}{2020}$

查看试题解析
2. 下列图形中，是轴对称图形，但不是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
3. 下列计算正确的是（）

A、﹣（a﹣b）=﹣a﹣b B、a²+a²=a⁴ C、a²•a³=a⁶ D、（ab²）²=a²b⁴

查看试题解析
4. 太阳中心的温度高达19200000℃，有科学记数法将19200000℃可表示为（　　）

A、1.92×10⁶ B、1.92×10⁷ C、19.2×10⁶ D、19.2×10⁷

查看试题解析
5. 一个立方体的表面展开图如图所示，将其折叠成立方体后，“你”字对面的字是（）

A、中 B、考 C、顺 D、利

查看试题解析
6. 如图，将一块含有30°角的直角三角板的两个顶点分别放在直尺的两条平行对边上，若∠α＝135°，则∠β等于（）

A、45° B、60° C、75° D、85°

查看试题解析
7. 下列命题正确的是（）

A、方程x²﹣x+1＝0有两个不相等实数根 B、对角线相等的四边形是矩形 C、平分弦的直径垂直于弦 D、等腰三角形底边上的中线平分顶角

查看试题解析
8. 在新型肺炎严重影响下，全国各地积极开展了“线上教学”，小明最近6天每天在线学习时长（单位：小时）分别为2，5，3，4，5，6，这组数据的众数、中位数分别是为（　　）

A、5，4.5 B、4，5 C、5，4 D、3，2

查看试题解析
9. 如图，在△ABC中，∠B＝70°，∠C＝30°，分别以点A和点C为圆心，大于 $\frac{1}{2}$ AC的长为半径画弧，两弧相交于点M、N ，作直线MN ，交BC于点D ，连接AD ，则∠BAD的度数为（）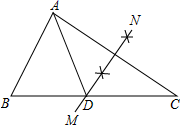

A、40° B、45° C、50° D、60°

查看试题解析
10. 2020年3月20日，深圳市民中心及周边楼宇为当日返回深圳的援鄂医疗队员亮灯，欢迎最美逆行者回家．小洪在欢迎英雄回家现场，如图，若他观测到英雄画像电子屏顶端A和底端C的仰角分别为∠α和∠β，小洪所站位置E到电子屏边缘AC垂直地面的B点距离为m米，那么英雄画像电子屏高AC为（　　）

A、 $(\frac{m}{\tan α} - \frac{m}{\tan β})$ 米 B、m•tan（α﹣β）米 C、m（tanα﹣tanβ）米 D、 $\frac{m}{\tan (α - β)}$ 米

查看试题解析
11. 如图，抛物线y＝ax²+bx+c经过点（﹣1，0），与y轴交于（0，2），抛物线的对称轴为直线x＝1，则下列结论中：①a+c＝b；②方程ax²+bx+c＝0的解为﹣1和3；③2a+b＝0；④c﹣a＞2，其中正确的结论有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
12. 已知正方形ABCD的边长为1，点P为正方形内一动点，若点M在AB上，且满足△PBC∽△PAM ，延长BP交AD于点N ，连结CM ．分析下列结论：①AP⊥BN；②BM＝DN；③点P一定在以CM为直径的圆上；④正方形内不存在点P使得PC＝ $\frac{\sqrt{5} - 1}{2}$ ．其中结论正确的个数是（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 分别写有数字 $\frac{1}{5}$ 、π、﹣1、0、 $\sqrt{3}$ 的五张大小和质地均相同的卡片，从中任意抽取一张，抽到无理数的概率是．

查看试题解析
14. 因式分解：x²﹣4= ．

查看试题解析
15. 如图，直线l经过第二、三、四象限，其解析式为y＝（m﹣2）x﹣m ，则m的取值范围为．

查看试题解析
16. 已知：如图，在平面直角坐标系xOy中，点A在x轴的正半轴上，点B、C在第一象限，且四边形OABC是平行四边形，AB＝2 $\sqrt{5}$ ，sinB＝ $\frac{2 \sqrt{5}}{5}$ ，反比例函数y＝ $\frac{k}{x}$ 的图象经过点C以及边AB的中点D ，则四边形OABC的面积为．

查看试题解析

三、解答题（共52分）

17. 计算： ${(\frac{1}{2})}^{- 3} + \tan 60^{0} + | \sqrt{3} - 2 | - {(- 2020)}^{0}$ ．

查看试题解析
18. 先化简： $(\frac{x^{2} - 3 x + 6}{x + 2} - 1) \div \frac{x^{2} - 4}{x^{3} + 4 x^{2} 4 x}$ ，然后在 $- \sqrt{3} \leq x \leq \sqrt{5}$ 内找一个你喜欢的整数代入求值．

查看试题解析
19. 2019年是新中国成立70周年，在“庆祝新中国成立70年华诞”主题教育活动月，深圳某学校组织开展了丰富多彩的活动，活动设置了“A：诗歌朗诵展演，B：歌舞表演，C：书画作品展览，D：手工作品展览”四个专项活动，每个学生限选一个专项活动参与．为了解活动开展情况，学校随机抽取了部分学生进行调查，并根据调查结果绘制了如图所示的不完整的条形统计图和扇形统计图：

(1)、本次随机调查的学生人数是人；

(2)、请你补全条形统计图；

(3)、在扇形统计图中，“B”所在扇形的圆心角为度．

(4)、小涛和小华各自随机参与其中的一个专项活动，请你用画树状图或列表的方式求他们恰好选中同一个专项活动的概率．

查看试题解析

20. 甲、乙两个药店销售同一种口罩，在甲药店，不论一次购买数量是多少，价格均为3元/个；在乙药店，一次性购买数量不超过100个时，价格为3.5元/个；一次性购买数量超过100个时，其中100个的价格仍为3.5元/个，超过100个的部分的价格为2.5元/个．

(1)、根据题意填表：

一次性购买数量（个）	50	100	150
甲药店花费（元）		300
乙药店花费（元）		300

(2)、当一次性购买多少个口罩时，在乙药店购买比在甲药店购买可以节约100元？

查看试题解析

21. 如图，E ， F分别是正方形ABCD的边CB ， DC延长线上的点，且BE＝CF ，过点E作EG∥BF ，交正方形外角的平分线CG于点G ，连接GF ．

(1)、求∠AEG的度数；

(2)、求证：四边形BEGF是平行四边形．

查看试题解析
22. 如图1，直线y₁＝kx+3与双曲线y₂＝ $\frac{m^{2} - 13 m}{x}$ （x＞0）交于点P ， PA⊥x轴于点A ， PB⊥y轴于点B ，直线y₁＝kx+3分别交x轴、y轴于点C和点D ，且S_△DBP＝27， $\frac{O C}{C A} = \frac{1}{2}$ ．

(1)、求OD和AP的长；

(2)、求m的值；

(3)、如图2，点M为直线BP上的一个动点，连接CB、CM ，当△BCM为等腰三角形时，请直接写出点M的坐标．

查看试题解析
23. 如图1，经过点B（1，0）的抛物线y＝a（x+1）²﹣ $\frac{32}{9}$ 与y轴交于点C ，其顶点为点G ，过点C作y轴的垂线交抛物线对称轴于点D ，线段CO上有一动点M ，连接DM、DG ．

(1)、求抛物线的表达式；

(2)、求GD+DM+ $\frac{\sqrt{2}}{2}$ MO的最小值以及相应的点M的坐标；

(3)、如图2，在（2）的条件下，以点A（﹣2，0）为圆心，以AM长为半径作圆交x轴正半轴于点E ．在y轴正半轴上有一动点P ，直线PF与⊙A相切于点F ，连接EF交y轴于点N ，当PF∥BM时，求PN的长．

查看试题解析