浙江省台州市临海区2021年数学中考一模试卷
试卷更新日期:2021-06-04 类型:中考模拟
一、单选题
-
1. 下面四个环境保护图案,属于中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一种面粉的重量标识为“ ”,则下列面粉重量合格的是( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 有四张背面完全相同的卡片,正面分别标有数字2,3,4,5.从中任意抽取两张,则下列事件为不可能事件的是( )A、两张卡片的数字之和等于4 B、两张卡片的数字之和等于5 C、两张卡片的数字之和等于6 D、两张卡片的数字之和等于75. 如图,将 绕点 顺时针旋转 得到 ,则点 经过的路径长为( )
2. 一种面粉的重量标识为“ ”,则下列面粉重量合格的是( )A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 有四张背面完全相同的卡片,正面分别标有数字2,3,4,5.从中任意抽取两张,则下列事件为不可能事件的是( )A、两张卡片的数字之和等于4 B、两张卡片的数字之和等于5 C、两张卡片的数字之和等于6 D、两张卡片的数字之和等于75. 如图,将 绕点 顺时针旋转 得到 ,则点 经过的路径长为( ) A、 B、 C、 D、6. 若把分式 中的 同时扩大2倍,则分式的值( )A、是原来的2倍 B、是原来的 C、是原来的 D、不变7. 如图,为测量楼高 ,在适当位置竖立一根高 的标杆 ,并在同一时刻分别测得其落在地面上的影长 ,则楼高 为( )
A、 B、 C、 D、6. 若把分式 中的 同时扩大2倍,则分式的值( )A、是原来的2倍 B、是原来的 C、是原来的 D、不变7. 如图,为测量楼高 ,在适当位置竖立一根高 的标杆 ,并在同一时刻分别测得其落在地面上的影长 ,则楼高 为( ) A、 B、 C、 D、8. 如图,在 中,点 是 的中点,分别以点 为圆心,大于 的长为半径作弧,两弧交于 ,直线 交 于点 ,连接 .若 的周长为10,则 的周长为( )
A、 B、 C、 D、8. 如图,在 中,点 是 的中点,分别以点 为圆心,大于 的长为半径作弧,两弧交于 ,直线 交 于点 ,连接 .若 的周长为10,则 的周长为( )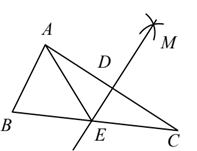 A、13 B、14 C、15 D、169. 路程 ,速度 ,时间 三者之间的关系式为 ,当其中一个量是常量时,另外两个变量的函数图象不可能是( )A、
A、13 B、14 C、15 D、169. 路程 ,速度 ,时间 三者之间的关系式为 ,当其中一个量是常量时,另外两个变量的函数图象不可能是( )A、 B、
B、 C、
C、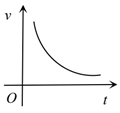 D、
D、 10. 四则运算符号有+,-,×,÷,现引入两个新运算符号∨,∧,合称“六则运算”. 的运算结果是 和 中较大的数, 的运算结果是 和 中较小的数.下列等式不一定成立的是( )A、 B、 C、 D、
10. 四则运算符号有+,-,×,÷,现引入两个新运算符号∨,∧,合称“六则运算”. 的运算结果是 和 中较大的数, 的运算结果是 和 中较小的数.下列等式不一定成立的是( )A、 B、 C、 D、二、填空题
-
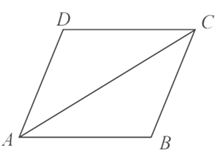
11. 请你写出一个大于1而小于5 的无理数.12. 盒子里有3支红色笔芯,2支黑色笔芯,每支笔芯除颜色外均相同.从中任意拿出一支笔芯,则拿出红色笔芯的概率是.13. 如图,菱形 中,已知 ,则 的度数为.
 14. 一种笔记本售价为6.3元/本,若一次性购买超过20本,则让利优惠,所买笔记本每本均按 元销售,要使让利后的销售额大于20本的销售额,则 的取值范围为.15. 若 是一次函数 图象上两个不同的点,且 ,则 .16. 如图, 是锐角三角形 的外接圆, ,且 ,点 是 高线的交点,连接 ,则 的度数为 , 的长为.
14. 一种笔记本售价为6.3元/本,若一次性购买超过20本,则让利优惠,所买笔记本每本均按 元销售,要使让利后的销售额大于20本的销售额,则 的取值范围为.15. 若 是一次函数 图象上两个不同的点,且 ,则 .16. 如图, 是锐角三角形 的外接圆, ,且 ,点 是 高线的交点,连接 ,则 的度数为 , 的长为.
三、解答题
-
17. 计算: .18. 解方程组:19. 临海大桥主塔是一个轴对称图形(如图所示),小明测得桥面宽度 米, ,求点 到桥面 的距离.(结果精确到0.1米,参考数据: )
 20. 如图,抛物线的顶点坐标为 ,且过点 .
20. 如图,抛物线的顶点坐标为 ,且过点 .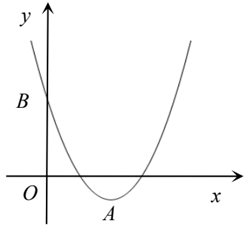 (1)、求抛物线的解析式;(2)、当 时,求 的取值范围.21. 4月23日是世界读书日,某校为了解七年级16个班级780名学生每周的课外阅读时间,随机抽取3个班级,每个班级10名学生.收集到每周用于课外阅读的时间(单位:分钟)相关数据如下:
(1)、求抛物线的解析式;(2)、当 时,求 的取值范围.21. 4月23日是世界读书日,某校为了解七年级16个班级780名学生每周的课外阅读时间,随机抽取3个班级,每个班级10名学生.收集到每周用于课外阅读的时间(单位:分钟)相关数据如下:甲班:20,30,30,30,30,50,70,100,110,130
乙班:40,40,60,60,60,70,80,100,120,130
丙班:20,20,20,40,50,70,110,130,140,140
分析数据得到部分统计量如下表:
班级
平均数
众数
中位数
甲班
60
30
40
乙班
76
65
丙班
74
20
(1)、表格中: ; ;(2)、根据统计数据,请对甲、乙、丙三个班级学生每周课外阅读的时间进行排名,并说出你的理由;(3)、估计该校七年级学生每周课外阅读时间至少60分钟大约多少人?22. 如图,⊙ 是 的外接圆,且 ,四边形 是平行四边形,边 与⊙ 交于点 ,连接 .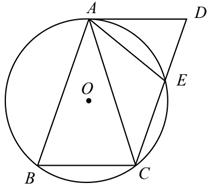 (1)、求证: ;(2)、若 ,求证:点 是 的中点.23. 在三角形中,一个角两夹边的平方和减去它对边的平方所得的差,叫做这个角的勾股差.
(1)、求证: ;(2)、若 ,求证:点 是 的中点.23. 在三角形中,一个角两夹边的平方和减去它对边的平方所得的差,叫做这个角的勾股差. (1)、概念理解:在直角三角形中,直角的勾股差为;在底边长为2的等腰三角形中,底角的勾股差为;(2)、性质探究:如图1, 是 的中线, ,记 中 的勾股差为 中 的勾股差为 ;
(1)、概念理解:在直角三角形中,直角的勾股差为;在底边长为2的等腰三角形中,底角的勾股差为;(2)、性质探究:如图1, 是 的中线, ,记 中 的勾股差为 中 的勾股差为 ;①求 的值(用含 的代数式表示);
②试说明 与 互为相反数;
(3)、性质应用:如图2,在四边形 中,点 与 分别是 与 的中点,连接 ,若 ,且 ,求 的值.24. (发现问题)小聪发现图1所示矩形甲与图2所示矩形乙的周长与面积满足关系: .
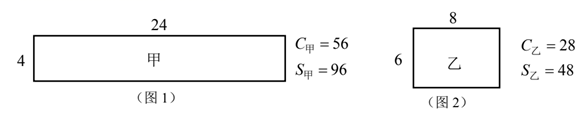
(提出问题)
对于任意一个矩形 ,是否一定存在矩形 ,使得 成立?
(解决问题)
(1)、对于图2所示的矩形乙,是否存在矩形丙(可设两条邻边长分别为 和 ),使得 成立.若存在,求出矩形丙的两条邻边长;若不存在,请说明理由;(2)、矩形 两条邻边长分别为 和1,若一定存在矩形 ,使得 成立,求 的取值范围;(3)、请你回答小聪提出来的问题.若一定存在,请说明理由;若不一定存在,请直接写出矩形 两条邻边长 满足什么条件时一定存在矩形 .