四川省广安市岳池县2021年数学中考二模试卷
试卷更新日期:2021-06-04 类型:中考模拟
一、单选题
-
1. 的算术平方根是( )A、 B、4 C、 D、22. 下列各运算中,计算正确的是( )A、2a·3a=6a2 B、 C、 D、3. 十三五,我国经济社会发展取得新的历史性成就.经济运行总体平稳,经济结构持续优化,国内生产总值从不到70万亿元增加到超过100万亿元.创新型国家建设成果丰硕,在载人航天、探月工程、深海工程、超级计算、量子信息等领域取得一批重大科技成果.脱贫攻坚成果举世瞩目,5575万农村贫困人口实现脱贫.用科学记数法表示100万亿为( )A、 B、 C、 D、4.
如图,是由6个棱长为1个单位的正方体摆放而成的,将正方体A向右平移2个单位,向后平移1个单位后,所得几何体的视图( )
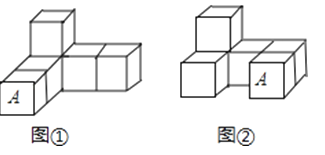 A、主视图改变,俯视图改变 B、主视图不变,俯视图不变 C、主视图不变,俯视图改变 D、主视图改变,俯视图不变5. 已知一组数据为:4,5,6,6,6,7,8.其平均数、中位数和众数的大小关系是( )A、众数=中位数=平均数 B、中位数<众数<平均数 C、平均数>中位数>众数 D、平均数<中位数<众数6. 已知 在第四象限,则 在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 抛物线y=﹣x2经过平移得到抛物线y=﹣(x+2)2﹣3,平移的方法是( )A、向左平移2个,再向下平移3个单位 B、向右平移2个,再向下平移3个单位 C、向左平移2个,再向上平移3个单位 D、向右平移2个,再向上平移3个单位8. 下列命题中,其逆命题是真命题的是( )A、两直线平行,内错角相等 B、对顶角相等 C、全等三角形的对应角相等 D、正方形的四条边相等9.
A、主视图改变,俯视图改变 B、主视图不变,俯视图不变 C、主视图不变,俯视图改变 D、主视图改变,俯视图不变5. 已知一组数据为:4,5,6,6,6,7,8.其平均数、中位数和众数的大小关系是( )A、众数=中位数=平均数 B、中位数<众数<平均数 C、平均数>中位数>众数 D、平均数<中位数<众数6. 已知 在第四象限,则 在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 抛物线y=﹣x2经过平移得到抛物线y=﹣(x+2)2﹣3,平移的方法是( )A、向左平移2个,再向下平移3个单位 B、向右平移2个,再向下平移3个单位 C、向左平移2个,再向上平移3个单位 D、向右平移2个,再向上平移3个单位8. 下列命题中,其逆命题是真命题的是( )A、两直线平行,内错角相等 B、对顶角相等 C、全等三角形的对应角相等 D、正方形的四条边相等9.如图,直径AB为12的半圆,绕A点逆时针旋转60°,此时点B旋转到点B′,则图中阴影部分的面积是( )
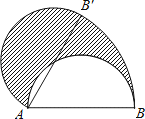 A、12π B、24π C、6π D、36π10. 如图所示是二次函数 图象的一部分,图象过 点(3,0),二次函数图象对称轴为 ,给出四个结论:① ;② ;③ ;④ ,其中正确结论有( )个.
A、12π B、24π C、6π D、36π10. 如图所示是二次函数 图象的一部分,图象过 点(3,0),二次函数图象对称轴为 ,给出四个结论:① ;② ;③ ;④ ,其中正确结论有( )个.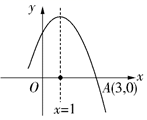 A、0 B、1 C、2 D、3
A、0 B、1 C、2 D、3二、填空题
-
11. 使代数式 有意义的x的取值范围是 .12. 因式分解: .13. 等腰三角形的两条边长分别为3和4,则这个等腰三角形的周长是 .14. 如图,五边形 是正五边形,若 ,则 .
 15. 请阅读材料,并解决实际问题:海伦—秦九韶公式:海伦(约公元 年),古希腊几何学家,在数学史上以解决几何测量问题闻名,在他的著作《度量》一书中证明了一个利用三角形的三条边的边长直接求三角形面积的公式:假设在平面内,有一个三角形的三条边长分别为 , , ,记 ,那么这个三角形的面积 .这个公式称海伦公式.秦九韶(约 — ),我国南宋时期的数学家,曾提出利用三角形的三边求面积的秦九韶公式 .它填补了中国数学史上的一个空白,从中可以看出中国古代已经具有很高的数学水平.通过公式变形,可以发现海伦公式和秦九韶公式实质是同一公式,所以海伦公式也称海伦—秦九韶公式.问题:在 中, , , ,用海伦—秦九韶公式求 的面积为.16. 在平面直角坐标系中,正方形 的位置如图所示,点 的坐标为 ,点 的坐标为 .延长 交 轴于点 ,作第 个正方形 ;延长 交 轴于点 ,作第 个正方形 ,…,按这样的规律进行下去,第 个正方形的面积是.
15. 请阅读材料,并解决实际问题:海伦—秦九韶公式:海伦(约公元 年),古希腊几何学家,在数学史上以解决几何测量问题闻名,在他的著作《度量》一书中证明了一个利用三角形的三条边的边长直接求三角形面积的公式:假设在平面内,有一个三角形的三条边长分别为 , , ,记 ,那么这个三角形的面积 .这个公式称海伦公式.秦九韶(约 — ),我国南宋时期的数学家,曾提出利用三角形的三边求面积的秦九韶公式 .它填补了中国数学史上的一个空白,从中可以看出中国古代已经具有很高的数学水平.通过公式变形,可以发现海伦公式和秦九韶公式实质是同一公式,所以海伦公式也称海伦—秦九韶公式.问题:在 中, , , ,用海伦—秦九韶公式求 的面积为.16. 在平面直角坐标系中,正方形 的位置如图所示,点 的坐标为 ,点 的坐标为 .延长 交 轴于点 ,作第 个正方形 ;延长 交 轴于点 ,作第 个正方形 ,…,按这样的规律进行下去,第 个正方形的面积是.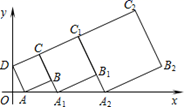
三、解答题
-
17. 计算:18. 解不等式组: .19. 先化简,再求值: ,其中 .20. 如图,一次函数 的图象与反比例函数 的图象相交于 两点,与 轴相交于点 .
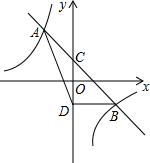 (1)、求一次函数与反比例函数的解析式;(2)、若点 与点 关于 轴对称,求 的面积;(3)、若 是反比例函数 上的两点,当 时,比 与 的大小关系.21. “中国梦”关系每个人的幸福生活,为展现巴中人追梦的风采,我市某中学举行“中国梦•我的梦”的演讲比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整,请你根据统计图解答下列问题.
(1)、求一次函数与反比例函数的解析式;(2)、若点 与点 关于 轴对称,求 的面积;(3)、若 是反比例函数 上的两点,当 时,比 与 的大小关系.21. “中国梦”关系每个人的幸福生活,为展现巴中人追梦的风采,我市某中学举行“中国梦•我的梦”的演讲比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整,请你根据统计图解答下列问题.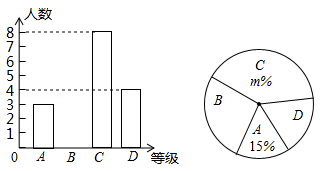 (1)、参加比赛的学生人数共有名,在扇形统计图中,表示“D等级”的扇形的圆心角为度,图中m的值为;(2)、补全条形统计图;(3)、组委会决定从本次比赛中获得A等级的学生中,选出2名去参加市中学生演讲比赛,已知A等级中男生有1名,请用“列表”或“画树状图”的方法求出所选2名学生中恰好是一名男生和一名女生的概率.22. 天水“伏羲文化节”商品交易会上,某商人将每件进价为8元的纪念品,按每件9元出售,每天可售出20件.他想采用提高售价的办法来增加利润,经实验,发现这种纪念品每件提价1元,每天的销售量会减少4件.(1)、写出每天所得的利润y(元)与售价x(元/件)之间的函数关系式.(2)、每件售价定为多少元,才能使一天所得的利润最大?最大利润是多少元?23. 如图,一堤坝的坡角∠ABC=60°,坡面长度AB=24米(图为横截面).为了使堤坝更加牢固,需要改变堤坝的坡面,为使得坡面的坡角∠ADB=50°,则应将堤坝底端向外拓宽(BD)多少米?(结果精确到0.1米)(参考数据: ≈1.73,sin50°≈0.77,cos50°≈0.64,tan50°≈1.20)
(1)、参加比赛的学生人数共有名,在扇形统计图中,表示“D等级”的扇形的圆心角为度,图中m的值为;(2)、补全条形统计图;(3)、组委会决定从本次比赛中获得A等级的学生中,选出2名去参加市中学生演讲比赛,已知A等级中男生有1名,请用“列表”或“画树状图”的方法求出所选2名学生中恰好是一名男生和一名女生的概率.22. 天水“伏羲文化节”商品交易会上,某商人将每件进价为8元的纪念品,按每件9元出售,每天可售出20件.他想采用提高售价的办法来增加利润,经实验,发现这种纪念品每件提价1元,每天的销售量会减少4件.(1)、写出每天所得的利润y(元)与售价x(元/件)之间的函数关系式.(2)、每件售价定为多少元,才能使一天所得的利润最大?最大利润是多少元?23. 如图,一堤坝的坡角∠ABC=60°,坡面长度AB=24米(图为横截面).为了使堤坝更加牢固,需要改变堤坝的坡面,为使得坡面的坡角∠ADB=50°,则应将堤坝底端向外拓宽(BD)多少米?(结果精确到0.1米)(参考数据: ≈1.73,sin50°≈0.77,cos50°≈0.64,tan50°≈1.20)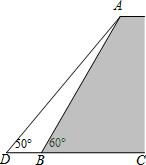 24. 在矩形 的 边上取一点 ,将 沿 翻折,使点 恰好落在 边上点 处.(1)、如图1,若 ,求 的度数;
24. 在矩形 的 边上取一点 ,将 沿 翻折,使点 恰好落在 边上点 处.(1)、如图1,若 ,求 的度数;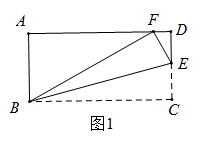 (2)、如图2,当 ,且 时,求 的长;
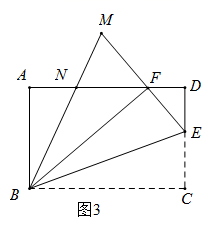
(2)、如图2,当 ,且 时,求 的长;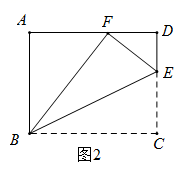 (3)、如图3,延长 ,与 的角平分线交于点 , 交 于点 ,当 时,求 出的值.
(3)、如图3,延长 ,与 的角平分线交于点 , 交 于点 ,当 时,求 出的值.