陕西省西安市经开区2021年数学中考一模试卷

试卷更新日期：2021-06-04 类型：中考模拟

进入出卷网下载

一、单选题

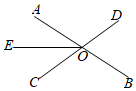
1. 如图，直线AB、CD相交于点O，OE平分∠AOC，若∠AOE＝35°，则∠BOC的度数是（）

A、110° B、50° C、60° D、70°

查看试题解析
2. 今年“五一”假期，我市某主题公园共接待游客77800人次，将77800用科学记数法表示为（）

A、 $0.778 \times 10^{5}$ B、 $7.78 \times 10^{4}$ C、 $77.8 \times 10^{3}$ D、 $778 \times 10^{2}$

查看试题解析
3. 给出四个实数 $\sqrt{5}$ ，2，0，-1，其中负数是（）

A、 $\sqrt{5}$ B、2 C、0 D、-1

查看试题解析
4. 下列计算正确的是（）

A、（﹣a+b）（﹣a﹣b）＝b²﹣a² B、x+2y＝3xy C、 $\sqrt{18}$ ﹣3 $\sqrt{2}$ ＝0 D、（﹣a³）²＝﹣a⁶

查看试题解析
5. 如图所示的网格由边长相同的小正方形组成，点A、B、C、D、E、F、G在小正方形的顶点上，则△ABC的重心是（）.

A、点D B、点E C、点F D、点G

查看试题解析
6. 若直线y＝kx+b（k≠0）经过点A（0，3），且与直线y＝mx﹣m（m≠0）始终交于同一点，则k的值为（）

A、3 B、﹣3 C、﹣1 D、2

查看试题解析
7. 如图，在边长为12的正方形ABCD中，有一个小正方形EFGH，其中E、 F、G分别在AB、BC、FD上，若BF=3，则小正方形边长为（）

A、6 B、5 C、 $\frac{15}{4}$ D、 $\sqrt{12}$

查看试题解析
8. 如图，点P为⊙O外一点，PA为⊙O的切线，A为切点，PO交⊙O于点B，∠P=30°，OB=3，则线段BP的长为（）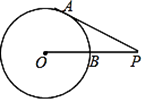

A、3 B、3 $\sqrt{3}$ C、6 D、9

查看试题解析
9. 函数y=ax²+2ax+m（a＜0）的图象过点（2，0），则使函数值y＜0成立的x的取值范围是（）

A、x＜﹣4或x＞2 B、﹣4＜x＜2 C、x＜0或x＞2 D、0＜x＜2

查看试题解析

二、填空题

10. 化简：（2+ $\sqrt{3}$ ）（2- $\sqrt{3}$ ）= .

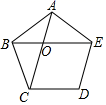
查看试题解析
11. 如图，正五边形ABCDE的边长为1，对角线AC、BE相交于点O，则四边形OCDE的周长为.

查看试题解析
12. 直线y＝kx(k＞0)与双曲线y＝ $\frac{6}{x}$ 交于A(x₁ ， y₁)和B(x₂ ， y₂)两点，则3x₁y₂－9x₂y₁的值为.

查看试题解析
13. 如图，在△ABC中，∠ACB＝90°，AB＝4，点O是AB的中点，以BC为直角边向外作等腰Rt△BCD，连接OD，当OD取最大值时，则∠ODB的度数是.

查看试题解析

三、解答题

14. 解不等式组 ${\begin{matrix} 2 (x - 1) \leq x + 2 \\ 5 x - 3 > 2 x \end{matrix}$ 并把解集在数轴上表示出来.

查看试题解析
15. 解分式方程： $\frac{x}{x - 2} - \frac{1}{x^{2} - 4} = 1$ ．

查看试题解析
16. 如图，在▱ABCD中，AC为对角线，且AC⊥AB.请用尺规作图法，作一个⊙O，使它经过A、C两点，且圆心O在BC边上.（保留作图痕迹，不写作法）

查看试题解析
17. 如图，在△ABC中，∠ABC＝90°，BD⊥AC于点D，点E在DB的延长线上，DE＝BC，∠1＝∠2，求证：DF＝AB.

查看试题解析

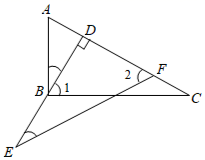18. 小西红柿又叫圣女果，既可以生吃，也可以作为美食原料，营养价值极高，因此深受大家欢迎.某水果商准备在甲、乙两个规模相当的小西红柿种植基地中选择一个进行长期合作，为了解这两个种植基地小西红柿的产量和产量的稳定性，从甲、乙两个种植基地中各随机选取一个大棚的小西红柿秧苗进行调查，过程如下，请补充完整.

收集数据：这两个大棚的小西红柿秧苗均为300株，各随机抽取25株，其收获期所产的小西红柿个数如下.

甲：27 35 46 55 48 36 47 68 82 48 57 66 75 27 36 57 57 66 58 61 71 38 47 46 71
乙：26 32 40 51 44 74 44 63 73 74 81 54 62 41 33 54 43 34 51 63 64 73 64 54 33

(1)、整理数据：按如表分组整理样本数据并补全表格.

个数（x）

株数

大棚

25≤x＜35

35≤x＜45

45≤x＜55

55≤x＜65

65≤x＜75

75≤x＜85

甲

乙

（说明：x＜45为产量不合格，x≥45为产量合格，45≤x＜65为产量良好，65≤x＜85为产量优秀）

分析数据：两组样本数据的平均数、众数和方差如表，并补全表格.

大棚	平均数	众数	方差
甲	53		215.04
乙		54	236.24

(2)、得出结论：估计乙种植基地的一个大棚中收获期产量良好的秧苗为株；

(3)、该水果商应选择种植基地进行长期合作，理由是（至少从两个不同角度说明）.

查看试题解析

19. 如图，五一假期，小华想用所学知识测得山脚B点到山顶C点登山缆车行驶的路线BC的距离，小华站在山脚B处测得C处的仰角为37°，然后，小华沿BA方向走了180米，移动至A点处，此时，测得C点处的仰角为30°，求山脚B点到山顶C点的距离BC.（结果保留根号）（参考数据sin37°≈ 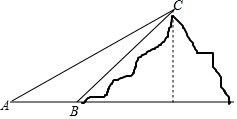$\frac{3}{5}$ ，cos37°≈ $\frac{4}{5}$ ，tan37°≈ $\frac{3}{4}$ ）

查看试题解析
20. 某单位计划周末组织员工去周边的某景点旅游，旅行社提供了以下收费方案：当旅游人数不超过10人时，人均费用为240元；当旅游人数超过10人但不超过25人时，与10人相比，每增加1人，人均费用降低6元；当旅游人数超过25人时，人均费用为150元.设参加旅游的人数为x人，人均费用为y元.

(1)、求y与x的函数关系式；

(2)、如果该公司这次参加旅游的人数有20人，那么总共需要支付给旅行社共多少元？

查看试题解析
21. 如图所示，甲、乙两人在玩转盘游戏时，分别把转盘A，B分成3等份和1等份，并在每一份内标上数字．游戏规则：同时转动两个转盘，当转盘停止后，指针所在区域的数字之积为奇数时，甲获胜；当数字之积为偶数时，乙获胜．如果指针恰好在分割线上时，则需重新转动转盘．

(1)、利用画树状图或列表的方法，求甲获胜的概率．

(2)、这个游戏规则对甲、乙双方公平吗？若公平，请说明理由；若不公平，请你在转盘A上只修改一个数字使游戏公平（不需要说明理由）．

查看试题解析
22. 如图，四边形ABCD内接于⊙O，对角线BD为⊙O直径，点E在BC延长线上，且∠E＝∠BAC.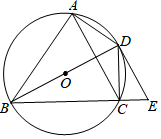

(1)、求证：DE是⊙O的切线；

(2)、若AC $//$ DE，当AB＝8，CE＝2，求⊙O的半径.

查看试题解析
23. 如图，抛物线y＝x²﹣2x﹣8与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，连接AC，BC.点P是第四象限内抛物线上的一个动点，点P的横坐标为m，过点P作PM⊥x轴，垂足为点M，PM交BC于点Q.

(1)、求A，B，C三点的坐标；

(2)、试探究在点P运动的过程中，是否存在这样的点Q，使得以A、C、Q为顶点的三角形是等腰三角形？若存在，请求出此时点Q的坐标；若不存在，请说明理由.

查看试题解析
24.

(1)、问题提出
如图①，在Rt△ABC中，∠A＝90°，AB＝3，AC＝4，在BC上找一点D，使得AD将△ABC分成面积相等的两部分，作出线段AD，并求出AD的长度；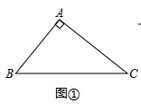

(2)、问题探究
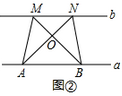
如图②，点A、B在直线a上，点M、N在直线b上，且a∥b，连接AN、BM交于点O，连接AM、BN，试判断△AOM与△BON的面积关系，并说明你的理由；

(3)、解决问题
如图③，刘老伯有一个形状为筝形OACB的养鸡场，在平面直角坐标系中，O（0，0）、A（4，0）、B（0，4）、C（6，6），是否在边AC上存在一点P，使得过B、P两点修一道笔直的墙（墙的宽度不计），将这个养鸡场分成面积相等的两部分？若存在，请求出直线BP的表达式；若不存在，请说明理由.

查看试题解析