广西南宁市马山县2021年数学中考一模试卷
试卷更新日期:2021-06-04 类型:中考模拟
一、单选题
-
1. 有理数2,1,﹣1,0中,最小的数是( )A、2 B、1 C、﹣1 D、02. 下面四个几何体中,左视图为圆的是( )A、
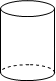 B、
B、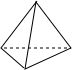 C、
C、 D、
D、 3. 某种细菌的半径是0.00000618米,用科学记数法把半径表示为( )A、618× B、6.18×10﹣7 C、6.18×106 D、6.18×4. 下列事件中,为必然事件的是( )A、明天要下雨 B、太阳从东边升起 C、﹣2>﹣1 D、打开电视机,它正在播广告5. 下列运算一定正确的是( )A、a2+a2=a4 B、a2•a4=a8 C、(a2)4=a8 D、(a+b)2=a2+b26. 在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.若随机摸出一个小球后不放回,再随机摸出一个小球,则两次取出小球标号的和等于5的概率为( )A、 B、 C、 D、7. 一副直角三角板如图放置,点C在FD的延长线上,AB//CF,∠F=∠ACB=90°,则∠DBC的度数为( )
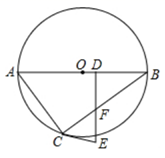
3. 某种细菌的半径是0.00000618米,用科学记数法把半径表示为( )A、618× B、6.18×10﹣7 C、6.18×106 D、6.18×4. 下列事件中,为必然事件的是( )A、明天要下雨 B、太阳从东边升起 C、﹣2>﹣1 D、打开电视机,它正在播广告5. 下列运算一定正确的是( )A、a2+a2=a4 B、a2•a4=a8 C、(a2)4=a8 D、(a+b)2=a2+b26. 在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.若随机摸出一个小球后不放回,再随机摸出一个小球,则两次取出小球标号的和等于5的概率为( )A、 B、 C、 D、7. 一副直角三角板如图放置,点C在FD的延长线上,AB//CF,∠F=∠ACB=90°,则∠DBC的度数为( ) A、10° B、15° C、18° D、30°8. 如图,已知 ,以 两点为圆心,大于 的长为半径画圆,两弧相交于点 ,连接 与 相较于点 ,则 的周长为( )
A、10° B、15° C、18° D、30°8. 如图,已知 ,以 两点为圆心,大于 的长为半径画圆,两弧相交于点 ,连接 与 相较于点 ,则 的周长为( ) A、8 B、10 C、11 D、139. 国家实施”精准扶贫“政策以来,很多贫困人口走向了致富的道路.某地区2016年底有贫困人口9万人,通过社会各界的努力,2018年底贫困人口减少至1万人.设2016年底至2018年底该地区贫困人口的年平均下降率为 ,根据题意列方程得( )A、 B、 C、 D、10. 如图,点A是反比例函数y 图象上的一点,过点A作AC⊥x轴,垂足为点C,D为AC的中点,若△AOD的面积为1,则k的值为( )
A、8 B、10 C、11 D、139. 国家实施”精准扶贫“政策以来,很多贫困人口走向了致富的道路.某地区2016年底有贫困人口9万人,通过社会各界的努力,2018年底贫困人口减少至1万人.设2016年底至2018年底该地区贫困人口的年平均下降率为 ,根据题意列方程得( )A、 B、 C、 D、10. 如图,点A是反比例函数y 图象上的一点,过点A作AC⊥x轴,垂足为点C,D为AC的中点,若△AOD的面积为1,则k的值为( )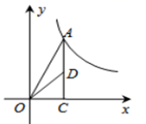 A、 B、﹣4 C、4 D、11. 如图,圆内接正六边形的边长为4,以其各边为直径作半圆,则图中阴影部分的面积为( )
A、 B、﹣4 C、4 D、11. 如图,圆内接正六边形的边长为4,以其各边为直径作半圆,则图中阴影部分的面积为( ) A、 B、 C、 D、12. 如图,在Rt△ABC中,∠C=90°,点E在AC边上.将∠A沿直线BE翻折,点A落在点A'处,连接A'B,交AC于点F.若A'E⊥AE,cosA= ,则 ( )
A、 B、 C、 D、12. 如图,在Rt△ABC中,∠C=90°,点E在AC边上.将∠A沿直线BE翻折,点A落在点A'处,连接A'B,交AC于点F.若A'E⊥AE,cosA= ,则 ( )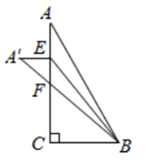 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 若代数式 有意义,则实数x的取值范围是.14. ﹣m=15. 在平面直角坐标系中,将 以点 为位似中心, 为位似比作位似变换,得到 .已知 ,则点 的坐标是 .
 16. 某校招聘教师,其中一名教师的笔试成绩是80分,面试成绩是60分,综合成绩笔试占60%,面试占40%,则该教师的综合成绩为分.17. 有一列数,按一定的规律排列成 ,-1,3,-9,27,-8181,….若其中某三个相邻数的和是-567,则这三个数中第一个数是.18. 如图,在正方形ABCD中,对角线AC与BD交于点O,点E在CD的延长线上,连接AE,点F是AE的中点,连接OF交AD于点G.若DE=2,OF=3,则点A到DF的距离为.
16. 某校招聘教师,其中一名教师的笔试成绩是80分,面试成绩是60分,综合成绩笔试占60%,面试占40%,则该教师的综合成绩为分.17. 有一列数,按一定的规律排列成 ,-1,3,-9,27,-8181,….若其中某三个相邻数的和是-567,则这三个数中第一个数是.18. 如图,在正方形ABCD中,对角线AC与BD交于点O,点E在CD的延长线上,连接AE,点F是AE的中点,连接OF交AD于点G.若DE=2,OF=3,则点A到DF的距离为.
三、解答题
-
19. 计算20. 解不等式组 ,并把解集在数轴上表示出来21. 每年的4月15日是我国全民国家安全教育日.某中学在全校七、八年级共800名学生中开展“国家安全法”知识竞赛,并从七、八年级学生中各抽取20名学生统计这部分学生的竞赛成绩(竞赛成绩均为整数,满分10分,6分及以上为合格).相关数据统计、整理如下:
八年级抽取的学生的竞赛成绩:4,4,6,6,6,6,7,7,7,8,8,8,8,8,8,9,9,9,10,10.
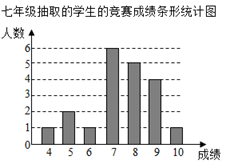
七,八年级抽取的学生的竞赛成绩统计表
年级
七年级
八年级
平均数
7.4
7.4
中位数
3
b
众数
7
c
合格率
85%
90%
根据以上信息,解答下列问题:
(1)、填空:a= , b= , c=.(2)、估计该校七、八年级共800名学生中竞赛成绩达到9分及以上的人数;(3)、比较样本数据,你认为哪个年级的成绩比较好?请说明理由(写出一条理由即可);22. 如图,菱形ABCD中,作BE⊥AD、CF⊥AB,分别交AD、AB的延长线于点E、F.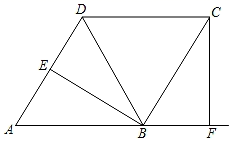 (1)、求证:AE=BF;(2)、若点E恰好是AD的中点,AB=2,求BD的值.23. 如图,吊车在水平地面上吊起货物时,吊绳BC与地面保持垂直,吊臂AB与水平线的夹角为64°,吊臂底部A距地面1.5m.(计算结果精确到0.1m,参考数据sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)
(1)、求证:AE=BF;(2)、若点E恰好是AD的中点,AB=2,求BD的值.23. 如图,吊车在水平地面上吊起货物时,吊绳BC与地面保持垂直,吊臂AB与水平线的夹角为64°,吊臂底部A距地面1.5m.(计算结果精确到0.1m,参考数据sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)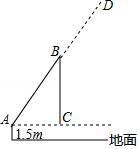 (1)、当吊臂底部A与货物的水平距离AC为5m时,吊臂AB的长为多少m.(2)、如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是多少?(吊钩的长度与货物的高度忽略不计)24. 上林大米被国家质检总局批准为地理标志保护产品,是广西首个列入地理标志保护的大米产品,大米在销售前需要一系列的加工过程,现需要150吨的水稻运往某大米工厂,且有甲、乙两种货车可供选择,配送公司提供了两种送货方案选择,如下表所示:
(1)、当吊臂底部A与货物的水平距离AC为5m时,吊臂AB的长为多少m.(2)、如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是多少?(吊钩的长度与货物的高度忽略不计)24. 上林大米被国家质检总局批准为地理标志保护产品,是广西首个列入地理标志保护的大米产品,大米在销售前需要一系列的加工过程,现需要150吨的水稻运往某大米工厂,且有甲、乙两种货车可供选择,配送公司提供了两种送货方案选择,如下表所示:方案一
方案二
甲种货车(辆)
2
1
乙种货车(辆)
1
2
运输吨数(吨)
20
22
(1)、一辆甲种货车和一辆乙种货车满载时可分别运货多少吨?(2)、决定调用甲、乙两种货车若干辆,并且均满载时一次可运水稻150吨,设调用甲种货车 辆,乙种货车 ( )辆,请用含 的代数式表示 :(3)、已知甲种货车的运费为600元/辆,乙种货车的运费为1000元/辆,在(2)的条件下,求运输150吨水稻的总运费 的最小值.