广西北部湾经济区2021年数学初中学业水平考试模拟试卷
试卷更新日期:2021-06-04 类型:中考模拟
一、单选题
-
1. -2的倒数是( )A、 B、2 C、-2 D、2. 如图,将直角三角形绕其一条直角边所在直线l旋转一周,得到的几何体是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 今年的新冠肺炎病毒侵袭武汉时,全中国第一时间组织对武汉的救援.这其中,我国自主研制的大型运输机“运20”,为在疫情初期向武汉快速转运大量物资和人员作出了重要贡献.“运20”起飞重量220吨,从立项到成功编入部队,经历了20多年,仅研究初期的预研经费就超过3 000 000 000元人民币.将3 000 000 000用科学记数法表示为( )A、3×108 B、0.3×1010 C、3×109 D、30×1084. 如图是某市5月上旬一周的天气情况,根据这一周中每天的最高气温绘制了折线统计图,这一周最高气温的平均温度是( )
3. 今年的新冠肺炎病毒侵袭武汉时,全中国第一时间组织对武汉的救援.这其中,我国自主研制的大型运输机“运20”,为在疫情初期向武汉快速转运大量物资和人员作出了重要贡献.“运20”起飞重量220吨,从立项到成功编入部队,经历了20多年,仅研究初期的预研经费就超过3 000 000 000元人民币.将3 000 000 000用科学记数法表示为( )A、3×108 B、0.3×1010 C、3×109 D、30×1084. 如图是某市5月上旬一周的天气情况,根据这一周中每天的最高气温绘制了折线统计图,这一周最高气温的平均温度是( )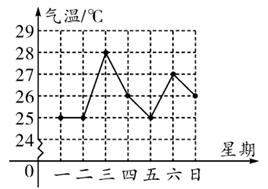 A、 B、 C、 D、5. 一把直尺和一块含30°角的直角三角板ABC如图所示摆放,直尺一边与三角板的两直角边分别交于点D和点E,另一边与三角板的两直角边分别交于点F和点A,且∠CED=35°,那么∠BAF的大小为( )
A、 B、 C、 D、5. 一把直尺和一块含30°角的直角三角板ABC如图所示摆放,直尺一边与三角板的两直角边分别交于点D和点E,另一边与三角板的两直角边分别交于点F和点A,且∠CED=35°,那么∠BAF的大小为( )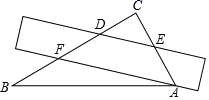 A、5° B、15° C、25° D、35°6. 下列各运算中,计算正确的是( )A、a+a=a2 B、(3a2)3=9a6 C、(a+b)2=a2+b2 D、2a•3a=6a27. 已知▱ABCD,根据图中尺规作图的痕迹,判断下列结论中不一定成立的是( )
A、5° B、15° C、25° D、35°6. 下列各运算中,计算正确的是( )A、a+a=a2 B、(3a2)3=9a6 C、(a+b)2=a2+b2 D、2a•3a=6a27. 已知▱ABCD,根据图中尺规作图的痕迹,判断下列结论中不一定成立的是( ) A、DE=BE B、∠DEA= ∠DAB C、∠DEA=∠BAE D、AD=DE8. 将分别标有“武”汉”加油”汉字的四个小球装在一个不透明的口袋中,这些球除汉字外无其他差别,每次摸球前先搅拌均匀,随机摸出一球,不放回:再随机摸出一球,两次摸出的球上的汉字能组成“加油"的概率是( )A、 B、 C、 D、9. 将抛物线y=x2-2x+1向下平移2个单位,再向左平移1个单位,所得抛物线的解析式是( )A、y=x2-2x-1 B、y=x2+2x-1 C、y=x2-2 D、y=x2+210. 抗击“新冠肺炎”疫情中,某呼吸机厂家接到一份生产300台呼吸机的订单,在生产完成一半时,应客户要求,需提前供货,每天比原来多生产20台呼吸机,结果提前2天完成任务.设原来每天生产x台呼吸机,下列列出的方程中正确的是( )A、 + = ﹣2 B、 + = +2 C、 = ﹣2 D、 = ﹣211. 如图,小刚在甲楼,他想利用最近所学知识测量对面的乙楼的高度,小刚在甲楼楼底 点测得乙楼楼顶 点的仰角为 ,当他爬上楼顶,在 点处测得乙楼 点的仰角为 ,若 , ,则乙楼的高度 为( ) .(参考数据: ,精确到 )
A、DE=BE B、∠DEA= ∠DAB C、∠DEA=∠BAE D、AD=DE8. 将分别标有“武”汉”加油”汉字的四个小球装在一个不透明的口袋中,这些球除汉字外无其他差别,每次摸球前先搅拌均匀,随机摸出一球,不放回:再随机摸出一球,两次摸出的球上的汉字能组成“加油"的概率是( )A、 B、 C、 D、9. 将抛物线y=x2-2x+1向下平移2个单位,再向左平移1个单位,所得抛物线的解析式是( )A、y=x2-2x-1 B、y=x2+2x-1 C、y=x2-2 D、y=x2+210. 抗击“新冠肺炎”疫情中,某呼吸机厂家接到一份生产300台呼吸机的订单,在生产完成一半时,应客户要求,需提前供货,每天比原来多生产20台呼吸机,结果提前2天完成任务.设原来每天生产x台呼吸机,下列列出的方程中正确的是( )A、 + = ﹣2 B、 + = +2 C、 = ﹣2 D、 = ﹣211. 如图,小刚在甲楼,他想利用最近所学知识测量对面的乙楼的高度,小刚在甲楼楼底 点测得乙楼楼顶 点的仰角为 ,当他爬上楼顶,在 点处测得乙楼 点的仰角为 ,若 , ,则乙楼的高度 为( ) .(参考数据: ,精确到 ) A、21.8 B、37.6 C、37.8 D、38.212. 如图,在矩形 中, .将 向内翻折,点 落在 上,记为 ,折痕为 .若将 沿 向内翻折,点 落在 上,记为 ,则 的长为( )
A、21.8 B、37.6 C、37.8 D、38.212. 如图,在矩形 中, .将 向内翻折,点 落在 上,记为 ,折痕为 .若将 沿 向内翻折,点 落在 上,记为 ,则 的长为( )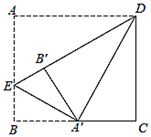 A、 B、1 C、2 D、
A、 B、1 C、2 D、二、填空题
-
13. 函数 的自变量 的取值范围是.14. 因式分解: .15. 某校,为从甲、乙两名初三学生中选出一人参加长沙市一中2020年生物夏令营海滨野外实习活动,特统计了他们最近10次生物考试成绩.其中,他们的平均成绩都为95分,方差分别是 =0.8, =1.3,从稳定性的角度来看,的成绩更稳定.(填“甲”或“乙”)16. 如图,在菱形 中, , 的垂直平分线交对角线 于点 ,垂足为 ,若 ,则菱形 的面积等于.
 17. 如图,已知点A在反比例函数y= (x<0)上,作Rt ABC,点D是斜边AC的中点,连接DB并延长交y轴于点E,若 BCE的面积为7,则k的值为.
17. 如图,已知点A在反比例函数y= (x<0)上,作Rt ABC,点D是斜边AC的中点,连接DB并延长交y轴于点E,若 BCE的面积为7,则k的值为. 18. 如图,在平面直角坐标系中,已知点 ,对△OAB连续作旋转变换,依次得到△1 , △2 , △3 , △4…,则△2022的直角顶点的坐标为.
18. 如图,在平面直角坐标系中,已知点 ,对△OAB连续作旋转变换,依次得到△1 , △2 , △3 , △4…,则△2022的直角顶点的坐标为.
三、解答题
-
19. 计算: .20. 先化简,后求值:(1﹣ )÷ ,其中x= +3.21. 如图,已知A(﹣3,3)、B(﹣4,1)、C(﹣1,1)是平面直角坐标系上的三点.
 (1)、请画出△ABC绕点O逆时针旋转90°后的△A1B1C1;(2)、请画出△A1B1C1关于y轴对称△A2B2C2;(3)、判断以A、A1、A2为顶点的三角形的形状.(无需说明理由)22. 为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
(1)、请画出△ABC绕点O逆时针旋转90°后的△A1B1C1;(2)、请画出△A1B1C1关于y轴对称△A2B2C2;(3)、判断以A、A1、A2为顶点的三角形的形状.(无需说明理由)22. 为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,79,81,71,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
七年级
0
1
0
a
7
1
八年级
1
0
0
7
b
2
分析数据:
平均数
众数
中位数
七年级
78
75
八年级
78
80.5
应用数据:
(1)、由上表填空:a= , b= , c= , d=.(2)、估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人?(3)、你认为哪个年级的学生对经典文化知识掌握的总体水平较好,请说明理由.23. 如图, 是 的直径, 为 的弦, , 与 的延长线交于点 ,点 在 上, 满足 . (1)、求证: 是 的切线;(2)、若 , , 求线段 的长.24. 某药店购进一批消毒液,计划每瓶标价100元,由于疫情得到有效控制,药店决定对这批消毒液全部降价销售,设每次降价的百分率相同,经过连续两次降价后,每瓶售价为81元.(1)、求每次降价的百分率.(2)、若按标价出售,每瓶能盈利100%,问第一次降价后销售消毒液100瓶,第二次降价后至少需要销售多少瓶,总利润才能超过5000元?25. 如图1,在正方形 中, 平分 ,交 于点 ,过点 作 ,交 的延长线于点 ,交 的延长线于点 .
(1)、求证: 是 的切线;(2)、若 , , 求线段 的长.24. 某药店购进一批消毒液,计划每瓶标价100元,由于疫情得到有效控制,药店决定对这批消毒液全部降价销售,设每次降价的百分率相同,经过连续两次降价后,每瓶售价为81元.(1)、求每次降价的百分率.(2)、若按标价出售,每瓶能盈利100%,问第一次降价后销售消毒液100瓶,第二次降价后至少需要销售多少瓶,总利润才能超过5000元?25. 如图1,在正方形 中, 平分 ,交 于点 ,过点 作 ,交 的延长线于点 ,交 的延长线于点 . (1)、求证: ;(2)、如图2,连接 、 ,求证: 平分 ;(3)、如图3,连接 交 于点 ,求 的值.26. 如图,抛物线y=ax2+bx+4交x轴于A(﹣3,0),B(4,0)两点,与y轴交于点C,连接AC,BC.点P是第一象限内抛物线上的一个动点,点P的横坐标为m,过点P作PM⊥x轴,垂足为点M,PM交BC于点Q.
(1)、求证: ;(2)、如图2,连接 、 ,求证: 平分 ;(3)、如图3,连接 交 于点 ,求 的值.26. 如图,抛物线y=ax2+bx+4交x轴于A(﹣3,0),B(4,0)两点,与y轴交于点C,连接AC,BC.点P是第一象限内抛物线上的一个动点,点P的横坐标为m,过点P作PM⊥x轴,垂足为点M,PM交BC于点Q.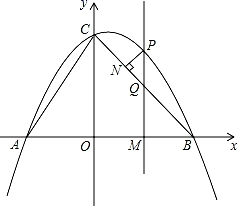 (1)、求此抛物线的表达式:(2)、过点P作PN⊥BC,垂足为点N,请用含m的代数式表示线段PN的长,并求出当m为何值时PN有最大值,最大值是多少?(3)、试探究点P在运动过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请求出此时点Q的坐标,若不存在,请说明理由.
(1)、求此抛物线的表达式:(2)、过点P作PN⊥BC,垂足为点N,请用含m的代数式表示线段PN的长,并求出当m为何值时PN有最大值,最大值是多少?(3)、试探究点P在运动过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请求出此时点Q的坐标,若不存在,请说明理由.