浙江省杭州市余杭区2020-2021学年七年级下学期数学期中考试试卷

试卷更新日期：2021-06-04 类型：期中考试

进入出卷网下载

一、选择题（共10小题）.

1. 下列计算正确的是（）

A、a³•a²＝a⁶ B、（b⁴）²＝b⁶ C、（xy）⁷＝xy⁷ D、x⁵+x⁵＝2x⁵

查看试题解析
2. 如图，下面哪个条件能判断DE∥BC的是（）

A、∠1＝∠2 B、∠4＝∠C C、∠1+∠3＝180° D、∠3+∠C＝180°

查看试题解析
3. 若关于x、y的方程ax+y＝2的一组解是 ${\begin{matrix} x = 4 \\ y = - 6 \end{matrix}$ ，则a的值为（）

A、﹣1 B、 $\frac{1}{2}$ C、1 D、2

查看试题解析
4. 如图，已知直线AB∥CD，∠GEB的平分线EF交CD于点F，∠1＝40°，则∠2等于（）

A、130° B、140° C、150° D、160°

查看试题解析
5. 若（x+5）（2x﹣n）＝2x²+mx﹣15，则（）

A、m＝7，n＝3 B、m＝7，n＝﹣3 C、m＝﹣7，n＝﹣3 D、m＝﹣7，n＝3

查看试题解析
6. 甲、乙两人从A地出发，沿同一方向练习跑步，如果甲让乙先跑10米，则甲跑5秒就可追上乙，如果甲让乙先跑2秒，那么甲跑4秒就能追上乙，设甲、乙每秒钟分别跑x米和y米，则可列方程组为（）

A、 ${\begin{matrix} 5 x = 5 y + 10 \\ 4 x - 2 = 4 y \end{matrix}$ B、 ${\begin{matrix} 5 x + 10 = 5 y \\ 4 x - 4 y = 2 \end{matrix}$ C、 ${\begin{matrix} 5 (x - y) = 10 \\ 4 (x - y) = 2 \end{matrix}$ D、 ${\begin{matrix} 5 x - 5 y = 10 \\ 4 (x - y) = 2 y \end{matrix}$

查看试题解析
7. 已知：2^m＝a，2ⁿ＝b，则2^2m+2n用a，b可以表示为（）

A、a²+b³ B、2a+3b C、a²b² D、6ab

查看试题解析
8. 使（x²+3x+p）（x²﹣qx+4）乘积中不含x²与x³项，则p+q的值为（）

A、8 B、﹣8 C、﹣2 D、﹣3

查看试题解析
9. 如图，直线AB∥CD，折线EFG交AB于M，交CD于N，点F在AB与CD之间，设∠AMF＝m°，∠EFG＝n°，则∠CNG的度数是（）

A、n° B、（m+n）° C、（2n﹣m）° D、（180+m﹣n）°

查看试题解析
10. 在关于x，y的二元一次方程组 ${\begin{matrix} x - 2 y = a + 6 \\ 3 x + y = 2 a \end{matrix}$ 的下列说法中，正确的是（）
①当a＝3时，方程的两根互为相反数；②当且仅当a＝﹣4时，解得x与y相等；③x，y满足关系式x+5y＝﹣12；④若9^x•27^y＝81，则a＝10.

A、①③ B、①② C、①②③ D、①②③④

查看试题解析

二、填空题：本大题有6个小题，每小题4分，共24分.

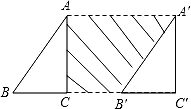
11. ﹣2（x²+x﹣2）＝.

查看试题解析
12. 如图，∠C＝90°，将直角三角形ABC沿着射线BC方向平移6cm，得三角形A′B′C′，已知BC＝3cm，AC＝4cm，则阴影部分的面积为cm².

查看试题解析
13. 对于任意实数a，b，定义关于“⊗”的一种运算如下：a⊗b＝2a﹣b.例如3⊗4＝2×3﹣4＝2.若x⊗y＝2，且y⊗x＝4，则x+y的值为.

查看试题解析
14. 已知关于x，y的二元一次方程组 ${\begin{matrix} 2 x + 3 y = k \\ x + 2 y = - 1 \end{matrix}$ 的解互为相反数，则k的值是．

查看试题解析
15. 已知x＝3^m+1，y＝1+9^m ，则用x的代数式表示y，结果为.

查看试题解析
16. 如图，EF∥AD∥BC，CE平分∠BCF，∠DAC＝120°，∠ACF＝20°，则∠FEC＝°.

查看试题解析

三、解答题：应写出解答过程、证明过程或演算步骤.

17. 化简：

(1)、（x+1）（x+2）

(2)、2a²b×（﹣3bc）

查看试题解析
18. 解下列二元一次方程组：

(1)、 ${\begin{cases} y = 4 x \\ 3 x + y = 14 \end{cases}$

(2)、 ${\begin{cases} 2 x + 5 y = 10 \\ 4 x - 3 (y + 1) = 4 \end{cases}$

查看试题解析
19. 先化简，再求值：

(1)、（x+1）²﹣（x+2）（x﹣3），其中x＝3.

(2)、已知2a²+3a﹣6＝0，求代数式3a（2a+1）﹣（2a+1）（2a﹣1）的值.

查看试题解析
20. 已知：如图，AB∥CD，BD平分∠ABC，CE平分∠DCF，∠ACE＝90°.

(1)、请问BD和CE是否平行？请你说明理由.

(2)、AC和BD的位置关系怎样？请说明判断的理由.

查看试题解析
21. 阅读：已知a+b＝﹣4，ab＝3，求a²+b²的值.
解：∵a+b＝﹣4，ab＝3，

∴a²+b²＝（a+b）²﹣2ab＝（﹣4）²﹣2×3＝10.

请你根据上述解题思路解答下面问题：

(1)、已知a﹣b＝﹣3，ab＝﹣2，求a²+b²的值.

(2)、已知（2018﹣a）（2019﹣a）＝2047，求（2018﹣a）²+（2019﹣a）²的值.

查看试题解析
22. 水果商贩老徐上水果批发市场进货，他了解到草莓的批发价格是每箱60元，苹果的批发价格是每箱40元.老徐购得草莓和苹果共60箱，刚好花费3100元.

(1)、问草莓、苹果各购买了多少箱？

(2)、老徐有甲、乙两家店铺，每售出一箱草莓和苹果，甲店分别获利15元和20元，乙店分别获利12元和16元.设老徐将购进的60箱水果分配给甲店草莓a箱，苹果b箱，其余均分配给乙店.由于他口碑良好，两家店都很快卖完了这批水果.
①若老徐在甲店获利600元，则他在乙店获利多少元？

②若老徐希望获得总利润为1000元，则a+b＝ ▲ .（直接写出答案）

查看试题解析
23. 已知，AB∥CD.点M在AB上，点N在CD上.

(1)、如图1中，∠BME、∠E、∠END的数量关系为：；（不需要证明）
如图2中，∠BMF、∠F、∠FND的数量关系为：；（不需要证明）

(2)、如图3中，NE平分∠FND，MB平分∠FME，且2∠E+∠F＝180°，求∠FME的度数；

(3)、如图4中，∠BME＝60°，EF平分∠MEN，NP平分∠END，且EQ∥NP，则∠FEQ的大小是否发生变化，若变化，请说明理由，若不变化，求出∠FEQ的度数.

查看试题解析