浙江省杭州市拱墅区2020-2021学年八年级下学期数学期中考试试卷

试卷更新日期：2021-06-04 类型：期中考试

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 下列方程中，是一元二次方程的是（）

A、ax²+bx+c＝0 B、x²+ $\frac{1}{x}$ ＝1 C、x²﹣1＝0 D、2x+3y﹣5＝0

查看试题解析
2. 下列医护图案既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列计算结果正确的是（）

A、 $\sqrt{5}$ ﹣ $\sqrt{2}$ ＝ $\sqrt{3}$ B、 $\sqrt{{(- 2)}^{2}}$ ＝﹣2 C、 $\sqrt{4 \frac{1}{9}}$ ＝2 $\frac{1}{3}$ D、（﹣2 $\sqrt{3}$ ）²＝12

查看试题解析
4. 平行四边形的两条对角线一定（）

A、互相垂直 B、互相平分 C、相等 D、以上都不对

查看试题解析
5. 若x=2能使下列二次根式有意义，则这个二次根式可以是（）

A、 $\sqrt{x - 1}$ B、 $\sqrt{1 - x}$ C、 $\sqrt{x - 3}$ D、 $\sqrt{- x}$

查看试题解析
6. 用反证法证明，“在△ABC中，∠A、∠B对边是a、b，若∠A＞∠B，则a＞b.”第一步应假设（）

A、a＜b B、a＝b C、a≤b D、a≥b

查看试题解析
7. 已知关于x的一元二次方程x²+bx+c＝0，其中b，c在数轴上的对应点如图所示，则这个方程的根的情况是（）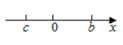

A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、只有一个实数根

查看试题解析
8. 如图，在四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（）

A、AB∥DC，AD∥BC B、AB∥DC，∠DAB＝∠DCB C、AO＝CO，AB＝DC D、AB∥DC，DO＝BO

查看试题解析
9. 实数a，b，c满足4a﹣2b+c＝0，则（）

A、b²﹣4ac＞0 B、b²﹣4ac≥0 C、b²﹣4ac＜0 D、b²﹣4ac≤0

查看试题解析
10. 如图，在平行四边形ABCD中，对角线AC、BD相交于点O，AC＝AB，E是AB边的中点，G、F为BC上的点，连接OG和EF，若AB＝26，BC＝20，GF＝10，则图中阴影部分的面积为（）

A、60 $\sqrt{3}$ B、20 $\sqrt{5}$ C、120 D、130

查看试题解析

二、填空题（共24分，每小题4分）

11. 若多边形的每一个外角都等于60°，则该多边形的边数是.

查看试题解析
12. 设x₁ ， x₂是一元二次方程x²﹣7x﹣5＝0的两个实数根，则x₁+x₂的值为.

查看试题解析
13. 若二次根式 $\sqrt{12}$ 与最简二次根式 $5 \sqrt{a + 1}$ 是同类二次根式，则a＝.

查看试题解析
14. 如图，在平行四边形ABCD中，E是边CD上一点，将△ADE沿AE折叠至△AD′E处，AD′与CE交于点F，若∠B＝53°，∠DAE＝20°，则∠FED′的度数为.

查看试题解析
15. 在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，点N是BC边上一点，点M为AB边上的动点，点D、E分别为CN，MN的中点，则DE的最小值是.

查看试题解析
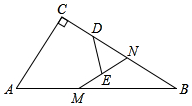16. 已知矩形ABCD的周长的平方与面积的比为18，则矩形ABCD的较长的一边与较短的一边的长度的比等于.

查看试题解析

三、解答题（本大题有7小题，共66分）

17. 计算：

(1)、 $\sqrt{18}$ ﹣2 $\sqrt{\frac{1}{2}}$ ；

(2)、（ $\frac{1}{2}$ ）^﹣²﹣（π﹣4）⁰+ $\frac{2}{2 + \sqrt{3}}$ .

查看试题解析
18. 解方程：

(1)、7x（5x+2）＝6（5x+2）；

(2)、 $\frac{x - 1}{2}$ ＝x²﹣1.

查看试题解析
19. 已知：如图，在▱ABCD中，点E、F分别在AD、BC上，EF与BD相交于点O，AE＝CF.求证：BD、EF互相平分.

查看试题解析
20. 某学校计划利用一片空地建一个学生自行车车棚，其中一面靠墙，这堵墙的长度为12米.计划建造车棚的面积为80平方米，已知现有的木板材料可使新建板墙的总长为28米.

(1)、这个车棚的长和宽分别应为多少米？

(2)、如图，为了方便学生取车，施工单位决定在车棚内修建几条等宽的小路，使得停放自行车的面积为54平方米，那么小路的宽度是多少米？

查看试题解析
21. 如图，在△ABC中，过点C作CD∥AB，E是AC的中点，连接DE并延长，交AB于点F，连接AD，CF.

(1)、求证：四边形AFCD是平行四边形；

(2)、若AB＝6，∠BAC＝60°，∠DCB＝135°，求AC的长.

查看试题解析
22. 已知方程x²+bx+a＝0①，和方程ax²+bx+1＝0②（a≠0）.

(1)、若方程①的根为x₁＝2，x₂＝3，求方程②的根；

(2)、当方程①有一根为x＝r时，求证x＝ $\frac{1}{r}$ 是方程②的根；

(3)、若a²b+b＝0，方程①的根是m与n，方程②的根是s和t，求 $\frac{m s}{n t}$ 的值.

查看试题解析
23. 如图，平行四边形ABCD的对角线AC，BD交于点O，AE平分∠BAD，交BC于点E，且∠ADC＝60°.

(1)、求证：AB＝AE；

(2)、若 $\frac{A B}{B C}$ ＝m（0＜m＜1），AC＝4 $\sqrt{3}$ ，连接OE；
①若m＝ $\frac{1}{2}$ ，求平行四边ABCD的面积；

②设 $\frac{S_{四边形 O E C D}}{S_{△ A O D}}$ ＝k，试求k与m满足的关系.

查看试题解析