浙江省杭州市2020-2021学年八年级下学期数学期中考试试卷

试卷更新日期：2021-06-04 类型：期中考试

进入出卷网下载

一、仔细选一选（本题有10个小题，每小题3分，共30分）

1. 二次根式 $\sqrt{x + 3}$ 有意义时，x的取值范围是（）

A、x≥﹣3 B、x＞﹣3 C、x≤﹣3 D、x≠﹣3

查看试题解析
2. 下面四个图标中，中心对称图形个数是（）

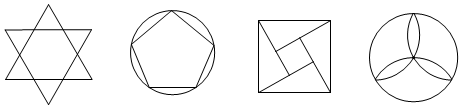A、0 B、1个 C、2个 D、3个

查看试题解析
3. 方程（x﹣1）（x+2）＝x﹣1的解是（）

A、x＝﹣2 B、x₁＝1，x₂＝﹣2 C、x₁＝﹣1，x₂＝1 D、x₁＝﹣1，x₂＝3

查看试题解析
4. 下列命题：① $\sqrt{x^{2} + 1}$ 是最简二次根式；②方程x²+4＝0有两个实数根；③一组数据1，2，3，4，4，10，若去掉10，剩下的数据与原数据相比，平均数变小，中位数和众数不变；④若一个多边形的内角和为1080°，则这个多边形为八边形.其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 用反证法证明“四边形中至少有一个内角大于或等于90°”时，应先假设（　　）

A、有一个内角小于90° B、有一个内角小于或等于90° C、每一个内角都小于90° D、每一个内角都大于90°

查看试题解析
6. 给出下列化简：① ${(- \sqrt{2})}^{2} = 2$ ；② $\sqrt{8} \times \sqrt{18} = 12$ ；③ $2 \sqrt{3} - \sqrt{3} = 1$ ；④ $\sqrt{3^{2} - 2^{2}} = \sqrt{3^{2}} - \sqrt{2^{2}} = 3 - 2 = 1$ ，其中正确的是（）

A、①②④ B、①②③ C、①② D、③④

查看试题解析
7. 某中学为了让学生的跳远在中考体育测试中取得满意的成绩，在锻炼一个月后，学校对九年级一班的45名学生进行测试，成绩如下表：
跳远成绩（cm）
160
170
180
190
200
220
人数
3
9
6
9
15
3
这些运动员跳远成绩的中位数和众数分别是（）

A、190，200 B、9，9 C、15，9 D、185，200

查看试题解析
8. 若一元二次方程x（kx+1）﹣x²+3＝0有实数根，则k的最大整数值是（）

A、2 B、1 C、0 D、﹣1

查看试题解析
9. 若关于x的一元二次方程ax²+bx+2＝0（a≠0）有一根为x＝2021，则一元二次方程a（x﹣1）²+bx﹣b＝﹣2必有一根为（）

A、2019 B、2020 C、2021 D、2022

查看试题解析
10. 如图，分别以Rt△ABC的斜边AB，直角边AC为边向外作等边△ABD和△ACE，F为AB的中点，DE，AB相交于点G，若∠BAC＝30°，下列结论：①EF⊥AC；②四边形ADFE为平行四边形；③AD＝4AG；④△DBF≌△EFA，其中正确结论的序号是（）

A、①②④ B、①③ C、②③④ D、①②③④

查看试题解析

二、认真填一填（本题有6个小题，每小题4分，共24分）

11. 在平面直角坐标系内，点A（ $\sqrt{5}$ ，2）关于原点中心对称的点的坐标是.

查看试题解析
12. 在平行四边形ABCD中，∠A＝45°，BC＝2，则AB与CD之间的距离为.

查看试题解析
13. 已知一组数据x₁ ， x₂ ， x₃的平均数是15，方差是2，那么另一组数据2x₁﹣4，2x₂﹣4，2x₃﹣4的平均数是.

查看试题解析
14. 若三角形的周长为10cm，则它的三条中位线组成的三角形的周长是 cm.

查看试题解析
15. 商场某种商品进价为120元/件，售价130元/件时，每天可销售70件；售价单价高于130元时，每涨价1元，日销售量就减少1件.据此，若销售单价为元时，商场每天盈利达1500元.

查看试题解析
16. 如图，在平行四边形ABCD中，∠B＜90°，BC＞AB，点E、F分别在边BC和CD上，AE＝6，AF＝8，∠EAF＝60°.

(1)、若AE⊥BC，AF⊥CD，则CD：BC＝；

(2)、若点E、F在分别是边BC和CD的中点，则AD＝.

查看试题解析

三、全面答一答（本题有7个小题，共66分）

17. 化简

(1)、 $\sqrt{8} - \sqrt{\frac{1}{2}} + \sqrt{18}$

(2)、 $\sqrt{27} \div \sqrt{3} - \sqrt{6} \times 3 \sqrt{2}$ .

查看试题解析
18. 解方程：

(1)、2x²﹣7x+3＝0；

(2)、（3x﹣4）²＝（4x﹣3）².

查看试题解析
19. 某中学举行“中国梦・校园好声音”歌手大赛，七年级和八年级根据初赛成绩，各选出5名选手组成年级代表队参加学校决赛，两个队各选出的5名选手的决赛成绩如图所示.

(1)、根据图示填写下表；

平均数（分）

中位数（分）

众数

七年级

85

八年级

85

100

(2)、哪一个代表队选手成绩较为稳定.

查看试题解析
20. 如图，在四边形ABCD中，AB∥CD，∠BAD的平分线AE交CD于点F，交BC的延长线于点E，且AB＝BE.

(1)、求证：四边形ABCD是平行四边形；

(2)、连接BF，若BF⊥AE，∠E＝60°，AB＝6，求四边形ABCD的面积.

查看试题解析
21. 已知：关于x的方程kx²﹣（4k﹣3）x+3k﹣3＝0

(1)、求证：无论k取何值，方程都有实根；

(2)、若x＝﹣1是该方程的一个根，求k的值；

(3)、若方程的两个实根均为正整数，求k的值（k为整数）.

查看试题解析
22. 某农场要建一个饲养场（矩形ABCD），两面靠墙（AD位置的墙最大可用长度为27米，AB位置的墙最大可用长度为15米），另两边用木栏围成，中间也用木栏隔开，分成两个场地及一处通道，并在如图所示的三处各留1米宽的门（不用木栏）.建成后木栏总长45米.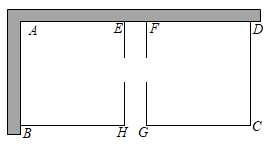

(1)、若饲养场（矩形ABCD）的一边CD长为8米，则另一边BC＝米.

(2)、若饲养场（矩形ABCD）的面积为180平方米，求边CD的长.

(3)、饲养场的面积能达到210平方米吗？若能达到，求出边CD的长；若不能达到，请说明理由.

查看试题解析
23. 如图1，在△ABC中，AB＝AC，∠ABC＝α，D是BC边上一点，以AD为边作△ADE，使AE＝AD，∠DAE+∠BAC＝180°.

(1)、若α＝50°，则∠ADE＝；

(2)、以AB，AE为边作平行四边形ABFE，
①如图2，若点F恰好落在DE上，求证：BD＝CD；

②如图3，若点F恰好落在BC上，求证：BD＝CF.

查看试题解析

	平均数（分）	中位数（分）	众数
七年级		85
八年级	85		100

跳远成绩（cm）	160	170	180	190	200	220
人数	3	9	6	9	15	3