浙江省绍兴市新昌县2020-2021学年七年级下学期数学期中考试试卷

试卷更新日期：2021-06-04 类型：期中考试

进入出卷网下载

一、选择题（共10小题，满分30分，每小题3分）

1. 下列方程中，属于二元一次方程的是（）

A、x+xy＝8 B、y＝x﹣1 C、x+ $\frac{1}{x}$ ＝2 D、x²﹣2x+1＝0

查看试题解析
2. 下列图中的“笑脸”，由如图平移得到的是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是（）

A、3x﹣x＝3 B、（x²）³＝x⁵ C、x²•x³＝x⁵ D、（2x）²＝2x²

查看试题解析
4. 下列图形中，能由∠1＝∠2得到AB∥CD的是（）

A、 B、 C、 D、

查看试题解析
5. 下列各式不能使用平方差公式的是（）

A、（2a+b）（2a﹣b） B、（﹣2a+b）（﹣2a﹣b） C、（2a﹣b）（-2a﹣b） D、（﹣2a+b）（b﹣2a）

查看试题解析
6. 若 $a^{x} = 3, a^{y} = 2$ ，则 $a^{2 x + y}$ 等于（）

A、18 B、 9 C、11 D、7

查看试题解析
7. 若关于x，y的方程组 ${\begin{matrix} 4 x - 3 y = 10 \\ k x + (k + 1) y = 8 \end{matrix}$ 的解中x的值比y的值大2，则k为（）

A、﹣3 B、1 C、﹣1 D、﹣2

查看试题解析
8. 我校跑操比赛中，某年级（1）班和（2）班的竞技实力相当，关于比赛结果，甲同学说：（1）班与（2）班得分比是6:5，乙同学说:(1)班的得分比(2)班得分的2倍少40分，若设（1）班得x分，（2）班得y分，根据题意，所列的方程组应为（）

A、 ${\begin{matrix} 6 x = 5 y \\ x = 2 y - 40 \end{matrix}$ B、 ${\begin{matrix} 6 x = 5 y \\ x = 2 y + 40 \end{matrix}$ C、 ${\begin{matrix} 5 x = 6 y \\ x = 2 y - 40 \end{matrix}$ D、 ${\begin{matrix} 5 x = 6 y \\ x = 2 y + 40 \end{matrix}$

查看试题解析
9. 如图，将一条对边互相平行的纸带进行两次折叠，折痕分别为AB、CD，若CD∥BE，∠1＝40°，则∠2的度数是（）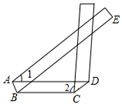

A、90° B、100° C、105° D、110°

查看试题解析
10. 如图，从边长为（a+1）cm的正方形纸片中剪去一个边长为（a﹣1）cm的正方形（a＞1），剩余部分沿虚线又剪拼成一个矩形（不重叠无缝隙），则该矩形的面积是（）

A、2 cm² B、2a cm² C、4a cm² D、（a²﹣1）cm²

查看试题解析

二、填空题（共6小题，满分18分，每小题3分）

11. 某种病毒的直径是0.00000008米，这个数据用科学记数法表示为米。

查看试题解析
12. 已知 ${\begin{matrix} x = 2 \\ y = - 3 \end{matrix}$ 是方程mx+3y=1的一个解，则m的值是．

查看试题解析
13. 如图，AD是∠EAC的平分线，AD∥BC，∠B＝30°，则∠C＝.

查看试题解析
14. 如图是一块长方形ABCD的场地，长AB＝a米，宽AD＝b米，从A、B两处入口的小路宽都为1米，两小路汇合处路宽为2米，其余部分种植草坪，则草坪面积为平方米.

查看试题解析
15. 如果多项式x²﹣2（m+1）xy+16y²是个完全平方式，则m＝.

查看试题解析
16. 观察下列图形：已知a∥b，在第一个图中，可得 $∠ 1 + ∠ 2 = 180^{\circ}$ ，则按照以上规律， $∠ 1 + ∠ 2 + ∠ p_{1} + \dots + ∠ p_{n} =$ 度 .

查看试题解析

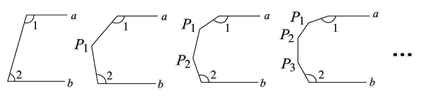
三、解答题（共7小题，满分40分。第17-20题每题6分，第21-题每题8分，第22-23每题10分）

17.

(1)、简便计算：2016²﹣2015×2017.

(2)、解方程组： ${\begin{matrix} 2 x = 3 y - 1 \\ 4 y = 2 x + 1 \end{matrix}$

查看试题解析
18. 先化简，再求值：
（x+2y）（x﹣2y）+（x﹣2y）²﹣（6x²y﹣2xy²）÷（2y），其中x＝﹣2，y＝ $\frac{1}{2}$ .

查看试题解析
19. 如图，在所给网格图（每个小格均为边长是1的正方形）中完成下列各题：

(1)、①△ABC经过平移后得到△A₁B₁C₁ ，请描述这个平移过程；
②过点C画AB的平行线CD；

(2)、求出△ABC的面积.

查看试题解析
20. 如图，AB与DE相交于点O，BC∥DE，∠B＝60°，∠D＝120°，AB与DF平行吗？说明你的理由.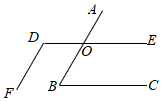

查看试题解析
21. “5.1”国际劳动节，某校决定组织甲乙两队参加义务劳动，并购买队服.下面是服装厂给出的服装的价格表：

购买服装的套数

1～39套

40～79套

80套及以上

每套服装的价格

80元

70元

60元

经调查：两个队共75人（甲队人数不少于40人），如果分别各自购买队服，两队共需花费5600元，请回答以下问题：

(1)、如果甲，乙两队联合起来购买服装，那么比各自购买服装最多可以节省.

(2)、甲、乙两队各有多少名学生？

查看试题解析
22.

(1)、计算下列各式，并寻找规律：
① $1 - \frac{1}{2^{2}}$ =（+）（-）=；

② $1 - \frac{1}{3^{2}}$ =（+）（-）=；

(2)、运用（1）中所发现的规，计算： $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) (1 - \frac{1}{5^{2}})$ ；

(3)、猜想 $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) \dots (1 - \frac{1}{9^{2}}) (1 - \frac{1}{10^{2}}) \dots (1 - \frac{1}{n^{2}})$ 的结果，并写出过程.

查看试题解析
23. [感知]：如图①，AB∥CD，∠AEP＝40°，∠PFD＝130°，求∠EPF的度数.小明想到了以下方法：
解：如图①，过点P作PM∥AB，

∴∠1＝∠AEP＝40°（两直线平行，内错角相等）

∵AB∥CD（已知），

∴PM∥CD（平行于同一条直线的两直线平行），

∴∠2+∠PFD＝180°（两直线平行，同旁内角互补）.

∵∠PFD＝130°（已知），

∴∠2＝180°﹣130°＝50°（等式的性质），

∴∠1+∠2＝40°+50°＝90°（等式的性质）.

即∠EPF＝90°（等量代换）.

(1)、[探究]如图②，AB∥CD，∠AEP＝50°，∠PFC＝120°，求∠EPF的度数.

(2)、[应用]如图③所示，在[探究]的条件下，∠PEA的平分线和∠PFC的平分线交于点G，求∠G的度数.

查看试题解析

购买服装的套数	1～39套	40～79套	80套及以上
每套服装的价格	80元	70元	60元