浙江省台州市2020-2021学年七年级下学期数学期中考试试卷
试卷更新日期:2021-06-04 类型:期中考试
一、选择题(共10小题,每小题3分,共30分)
-
1. 64的平方根是( )A、 8 B、-8 C、±8 D、42. 已知 是方程mx+y=3的解,则m的值( )A、2 B、-2 C、1 D、-13. 如图所示,下列结论中正确的是 ( )
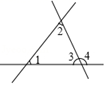 A、 和 是同位角 B、 和 是同旁内角 C、 和 是内错角 D、 和 是对顶角4. 平面直角坐标系中,点A(-1,0)在( )A、x轴的正半轴 B、x轴的负半轴 C、y轴的正半轴 D、y轴的负半轴5. 下列算式中能说明命题“两个无理数的和还是无理数”是假命题的是( )A、 B、 C、 D、6. 若关于x的不等式组的解集在数轴上如图所示,则这个不等式组可能是( )
A、 和 是同位角 B、 和 是同旁内角 C、 和 是内错角 D、 和 是对顶角4. 平面直角坐标系中,点A(-1,0)在( )A、x轴的正半轴 B、x轴的负半轴 C、y轴的正半轴 D、y轴的负半轴5. 下列算式中能说明命题“两个无理数的和还是无理数”是假命题的是( )A、 B、 C、 D、6. 若关于x的不等式组的解集在数轴上如图所示,则这个不等式组可能是( )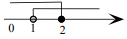 A、 B、 C、 D、7. 如果两个角的两边分别平行,而其中一个角比另一个角的3倍少20°,那么这两个角是( )A、50°、130° B、都是10° C、50°、130°或10°、10° D、以上都不对8. 已知 且x+y=3,则z的值为( )A、-3 B、-5 C、7 D、19. 小江去商店购买签字笔和笔记本(签字笔的单价相同,笔记本的单价相同).若购买20支签字笔和15本笔记本,则他身上的钱会差25元;若购买19支签字笔和13本笔记本,则他身上的钱会剩下15元.若小江购买17支签字笔和9本笔记本,则A、他身上的钱会不足95元 B、他身上的钱会剩下95元 C、他身上的钱会不足105元 D、他身上的钱会剩下105元10. 如图, 则 与 的数量关系是( )
A、 B、 C、 D、7. 如果两个角的两边分别平行,而其中一个角比另一个角的3倍少20°,那么这两个角是( )A、50°、130° B、都是10° C、50°、130°或10°、10° D、以上都不对8. 已知 且x+y=3,则z的值为( )A、-3 B、-5 C、7 D、19. 小江去商店购买签字笔和笔记本(签字笔的单价相同,笔记本的单价相同).若购买20支签字笔和15本笔记本,则他身上的钱会差25元;若购买19支签字笔和13本笔记本,则他身上的钱会剩下15元.若小江购买17支签字笔和9本笔记本,则A、他身上的钱会不足95元 B、他身上的钱会剩下95元 C、他身上的钱会不足105元 D、他身上的钱会剩下105元10. 如图, 则 与 的数量关系是( )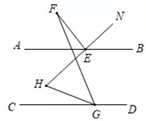 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,每小题4分,共24分)
-
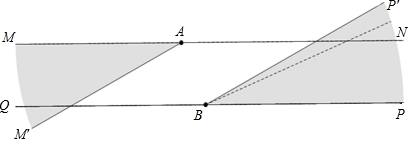
11. 的整数部分是。12. 已知x=1﹣t,y=2﹣3t,那么用含x的代数式表示y为.13. 点P(m,n)的坐标满足m+n<0,mn>0,则点P到x轴的距离为。14. 一艘货船沿着北偏西62º方向航行,为避免触礁,左拐28º后的航线是。15. 关于x的不等式组 的解集中每一个值均不在 的范围内,则a的取值范围是.16. 台州市旅游局为了亮化某景点,在两条笔直且互相平行的景观道MN、QP上分别放置A、B两盏激光灯,如图所示.A灯发出的光束自AM逆时针旋转至AN便立即回转;B灯发出的光束自BP逆时针旋转至BQ便立即回转,两灯不间断照射,A灯每秒转动12°,B灯每秒转动4°.B灯先转动12秒,A灯才开始转动.当B灯光束第一次到达BQ之前,两灯的光束互相平行时A灯旋转的时间是.
三、解答题(本大题共8个小题,第17题8分,第18、19、20题各6分,第21题8分,第22、23题各10分,第24题各12分,共66分)
-
17.(1)、计算:(2)、解方程组18. 解不等式组 ,并写出其所有的整数解.19. 已知 的算术平方根是3, 的立方根是-2,求 的平方根.20. 如图,已知 , ,求证: .完成推理填空:
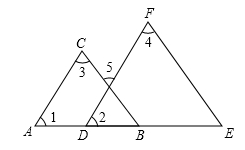
证明:∵ (已知),
_▲_,
_▲_ ( )
又 (已知),
_▲_( ),
( )
21. 如图,网格中每个小正方形的边长均为1个单位长度,已知A(-2,1)B(-2,-1),C(0,1)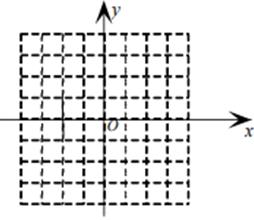 (1)、请在图中所示的平面直角坐标系中作出△ABC;(2)、把△ABC平移到△A1B1C1 , 使点A的对应点A1的坐标为(0,-2),请你作出△A1B1C1(点B1、点C1分别是顶点B、C的对应点);(3)、在如图所示的网格中,若△PBC与△ABC的面积相等,则满足条件的不与A重合的格点P(横纵坐标均为整数)共有个。22. 为了响应国家与新冠疫情斗争的号召,某校通过悬挂横幅与宣传牌进行专项宣传活动。 已知制作5条横幅与制作2块宣传牌的费用一样,制作2条横幅与3块宣传牌共需950元.(1)、求制作横幅与宣传牌的单价各是多少?(2)、学校计划共用2500元制作横幅和宣传牌,要求宣传牌不少于5块,请问:可以几种设计制作方案?(横幅和宣传牌都要有)23. 在数学课外小组活动中,老师提出了如下问题:
(1)、请在图中所示的平面直角坐标系中作出△ABC;(2)、把△ABC平移到△A1B1C1 , 使点A的对应点A1的坐标为(0,-2),请你作出△A1B1C1(点B1、点C1分别是顶点B、C的对应点);(3)、在如图所示的网格中,若△PBC与△ABC的面积相等,则满足条件的不与A重合的格点P(横纵坐标均为整数)共有个。22. 为了响应国家与新冠疫情斗争的号召,某校通过悬挂横幅与宣传牌进行专项宣传活动。 已知制作5条横幅与制作2块宣传牌的费用一样,制作2条横幅与3块宣传牌共需950元.(1)、求制作横幅与宣传牌的单价各是多少?(2)、学校计划共用2500元制作横幅和宣传牌,要求宣传牌不少于5块,请问:可以几种设计制作方案?(横幅和宣传牌都要有)23. 在数学课外小组活动中,老师提出了如下问题:如果一个不等式中含有绝对值,并且绝对值符号中含有未知数,我们把这样的不等式叫做绝对值不等式,求绝对值不等式|x|>3的解集.小方同学的探究过程如下:
先根据绝对值的定义,求出|x|恰好是3时x的值,并在数轴上表示为点A,B,如图所示。观察数轴发现,以点A,B为分界点把数轴分为三部分:
点A左边的点表示的数的绝对值大于3;
点A, B之间的点表示的数的绝对值小于3;
点B右边的点表示的数的绝对值大于3.
因此,小方同学得出结论 绝对值不等式|x|>3的解集为:x<-3或x>3
参照小方同学的思路,解决下列问题:
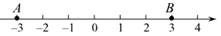 (1)、请你直接写出下列绝对值不等式的解集。
(1)、请你直接写出下列绝对值不等式的解集。① |x|>1的解集是;② |x|<2.5的解集是;
(2)、求绝对值不等式2|x-3|+5>13的解集.(3)、直接写出不等式x2>4的解集是。24. 已知△ABC, 交AC于点E, 交AB于点F.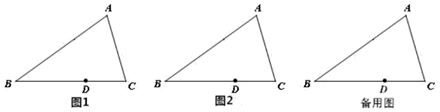 (1)、如图1,若点D在边BC上,
(1)、如图1,若点D在边BC上,①补全图形;
②求证: .
(2)、点G是线段AC上的一点,连接FG,DG.①若点G是线段AE
 中点,请你在图2中补全图形,判断 , , 之间的数量关系,并证明;
中点,请你在图2中补全图形,判断 , , 之间的数量关系,并证明;②若点G是线段EC上的一点,请你直接写出 , , 之间的数量关系.