浙江省绍兴市新昌县2020-2021学年八年级下学期数学期中联考试卷
试卷更新日期：2021-06-04 类型：期中考试
一、选择题（共10小题，每小题3分，共30分）.
-
1. 下列图形中，既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
2. 下列方程是一元二次方程的是（ ）A、﹣6x+2＝0 B、2x2﹣y+1＝0 C、x2+2x＝0 D、 +x＝23. 有一组数据： ，5， ， ， ， ， ，5，则这组数据的众数是（ ）A、 B、 C、 D、4. 正十二边形的外角和的度数为（ ）A、180° B、360° C、720° D、1800°5. 图中信息是小明和小华射箭的成绩，两人都射了10箭，则射箭成绩的方差较大的是（ ）
A、小明 B、小华 C、两人一样 D、无法确定6. 一元二次方程4x2﹣2x﹣1＝0的根的情况为（ ）A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根7. 将方程x2﹣6x+1＝0配方后，原方程变形为（ ）A、（x﹣3）2＝8 B、（x﹣3）2＝﹣8 C、（x﹣3）2＝9 D、（x﹣3）2＝﹣98. 如图，在△ABC中，点D，E分别是边AB，BC的中点，若△DBE的周长是7，则△ABC的周长是（ ）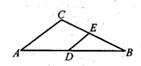
A、8 B、10 C、12． D、149. 在某篮球邀请赛中，参赛的每两个队之间都要比赛一场，共比赛36场.设有x个队参赛，根据题意，可列方程为（ ）A、 x（x﹣1）＝36 B、 x（x+1）＝36 C、x（x﹣1）＝36 D、x（x+1）＝3610. 如图，△ABC中，AB＝4，AC＝3，AD、AE分别是其角平分线和中线，过点C作CG⊥AD于F，交AB于G，连接EF，则线段EF的长为（ ）
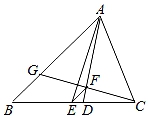A、1 B、 C、 D、二、填空题（共6小题，每小题3分，共18分）.
-
11. 化简 的结果是 ．12. 某组数据的方差计算公式为S2＝ [（x1﹣2）2+（x2﹣2）2+…+（x8﹣2）2]，则该组数据的样本容量是 ， 该组数据的平均数是 ．13. 某种产品原来售价为200元，经过连续两次大幅度降价处理，现按72元的售价销售．设平均每次降价的百分率为x，列出方程： ．14. 若y= ，则x+y= ．15. 如图，E是平行四边形ABCD边BC上一点，连接AE，并延长AE与DC的延长线交于点F，若AB＝AE，∠F＝50°，则∠D＝°.
16. 如图，在平行四边形ABCD中，连接BD，且BD＝CD，过点A作AM⊥BD于点M，过点D作DN⊥AB于点N，且DN＝4，在DB的延长线上取一点P，满足∠ABD＝∠MAP＋∠PAB，则AP＝.
三、解答题（共7题，共52分）
-
17.(1)、 ；(2)、 .18. 解下列方程：(1)、x2﹣4x﹣5＝0；(2)、5x（x+1）＝2（x+1）.19. 我校九年级有800名学生，在体育中考前进行一次排球模拟测试，从中随机抽取部分学生，根据其测试成绩制作了下面两个统计图，请根据相关信息，解答下列问题：
(1)、本次抽取到的学生人数为 ， 图2中m的值为；(2)、求出本次调查获取的样本数据的平均数、众数和中位数；(3)、根据样本数据，估计我校九年级模拟模拟体测中得12分的学生约有多少人？20. 已知关于x的方程x2+2x+m﹣2＝0.(1)、若该方程有两个不相等的实数根，求实数m的取值范围；(2)、当该方程的一个根为1时，求m的值及方程的另一根.21. 如图，在平行四边形ABCD中，点O是对角线BD的中点，过点O任作一条直线，分别与AD，BC交于点E，F.求证：四边形BEDF是平行四边形.
22. 商场将每件进价为80元的某种商品原来按每件100元出售，一天可售出100件.后来经过市场调查，发现这种商品单价每降低1元，其销量可增加10件.(1)、问商场经营该商品原来一天可获利润多少元？(2)、若商场经营该商品一天要获利润2160元，则每件商品售价应为多少元？23. 如图，在Rt△ABC中，∠C＝90°，BC＝6cm，AC＝8cm，点P从点C开始沿射线CA方向以1cm/s的速度运动；同时，点Q也从点C开始沿射线CB方向以3cm/s的速度运动．
(1)、几秒后△PCQ的面积为3cm2？此时PQ的长是多少？（结果用最简二次根式表示）(2)、几秒后以A、B、P、Q为顶点的四边形的面积为22cm2？