浙江省嘉兴市2020-2021学年七年级下学期数学期中考试试卷

试卷更新日期：2021-06-04 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程是二元一次方程的是（）

A、 $x + y = 2$ B、 $x y = 3$ C、 $x^{2} - 2 x = 1$ D、 $\frac{1}{x} = x - 2$

查看试题解析
2. 国产手机芯片麒麟980是全球首个7纳米制程芯片，已知1纳米 $= 0.000000001$ 米，则7纳米用科学记数法表示为（）

A、 $0.7 \times 10^{- 8}$ 米 B、 $0.7 \times 10^{- 9}$ 米 C、 $7 \times 10^{- 8}$ 米 D、 $7 \times 10^{- 9}$

查看试题解析
3. 如图，已知直线a，b被直线c所截，下列有关 $∠ 1$ 与 $∠ 2$ 说法正确的是（）

A、 $∠ 1$ 与 $∠ 2$ 是同位角 B、 $∠ 1$ 与 $∠ 2$ 是内错角 C、 $∠ 1$ 与 $∠ 2$ 是同旁内角 D、 $∠ 1$ 与 $∠ 2$ 是对顶角

查看试题解析
4. 下列各式从左到右的变形中，是因式分解的是（）

A、 $x^{2} - 4 - x = (x + 2) (x - 2) - x$ B、 $(x + 1) (x - 4) = x^{2} - 3 x - 4$ C、 $4 x^{2} + 4 x + 1 = {(2 x + 1)}^{2}$ D、 $x^{2} + 6 x = {(x + 3)}^{2} - 9$

查看试题解析
5. 下列计算：① $\frac{1}{3} m (m - 1) = \frac{1}{3} m^{2} - 1$ ；② $(m + 2) (m - 3) = m^{2} - 6$ ；③ ${(m - n)}^{2} = m^{2} - n^{2}$ ；④ $(m^{2} - 2 m n + m) \div m = m - 2 n + 1$ ，其中正确的是（）

A、① B、② C、③ D、④

查看试题解析
6. 《九章算术》是中国古代数学著作之一，书中有这样一个问题：五只雀、六只燕共重一斤，雀重燕轻，互换其中一只，恰好一样重.问：每只雀、燕的重量各为多少?设一只雀的重量为x斤，一只燕的重量为y斤，则可列方程组为（）

A、 ${\begin{cases} 5 x + 6 y = 1 \\ 5 x - y = 6 y - x \end{cases}$ B、 ${\begin{cases} 6 x + 5 y = 1 \\ 5 x + y = 6 y + x \end{cases}$ C、 ${\begin{cases} 5 x + 6 y = 1 \\ 4 x + y = 5 y + x \end{cases}$ D、 ${\begin{cases} 6 x + 5 y = 1 \\ 4 x - y = 5 y - x \end{cases}$

查看试题解析
7. 我们已经知道，整式可以分解成几个因式的积的形式，类比数的整除，整式也能被其每一个因式整除，下列多项式不能被 $x + 1$ 整除的是（）

A、 $x^{2} - 1$ B、 $2 x^{2} + 2 x$ C、 $x (x + 1) - x + 1$ D、 $x (x + 1) - 3 x - 3$

查看试题解析
8. 将一张边沿互相平行的纸条如图折叠后，若边 $A D / / B C$ ，则翻折角 $∠ 1$ 与 $∠ 2$ 一定满足的关系是（）

A、 $∠ 1 = 2 ∠ 2$ B、 $∠ 1 + ∠ 2 = 90 °$ C、 $∠ 1 - ∠ 2 = 30 °$ D、 $2 ∠ 1 - 3 ∠ 2 = 30 °$

查看试题解析
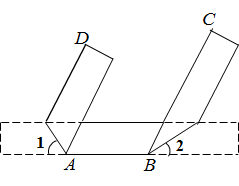9. 已知整式① $s^{2} - 4 t^{2} - 2 t - 1$ ，② $s^{2} - 2 s t - 2 t - 1$ ，若 $s = 2 t + 1$ ，则下列说法正确的是（）

A、①与②的和是常数 B、①与②的差是常数 C、①与②的积是常数 D、①与②的和、差、积都与t的值有关

查看试题解析
10. 小明去文具店购买了笔和本子共5件，已知两种文具的单价均为正整数且本子的单价比笔的单价贵.在付账时，小明问是不是27元，但收银员却说一共48元，小明仔细看了看后发现自己将两种商品的单价记反了.小明实际的购买情况是（）

A、1支笔，4本本子 B、2支笔，3本本子 C、3支笔，2本本子 D、4支笔，1本本子

查看试题解析

二、填空题

11. 因式分解m³﹣4m＝.

查看试题解析
12. 计算： $(- a^{3} + 8 a) \div 4 a =$ .

查看试题解析
13. 已知二元一次方程 $3 x - 4 y = 2$ .用关于x的代数式表示y，则 $y =$ .

查看试题解析
14. 如图，直线 $l_{1} ， l_{2}$ 被 $l_{3}$ 所截，下列条件：① $∠ 1 = ∠ 2$ ；② $∠ 3 = ∠ 4$ ；③ $l_{1} / / l_{2}$ ，其中能判断 $A C / / B D$ 的一个条件是.

查看试题解析
15. 已知 ${\begin{array}{l} x = 3 \\ y = - 1 \end{array}$ 是二元一次方程 $m x - 2 y = 3$ 的一个解，则m的值为.

查看试题解析

16. 如表是一组密码的一部分，目前已破译出“守初心”的对应口令是“担使命”，根据上述破译方法，破译出“找差距”的对应口令是.

落	市	担	山	七	牢	七
中	湖	为	就	吴	命	金
使	差	圾	守	立	实	华
人	忘	兴	水	分	是	心
抓	初	成	民	银	垃	距
共	青	祝	区	类	年	记
庆	找	周	和	国	州	绿

查看试题解析

17. 已知 ${(2^{x})}^{2} = 2^{y} \times 2^{3}$ ，则 $y - 2 x =$ .

查看试题解析
18. 定义：对于三个不是同类项的单项式A，B，C，若 $A + B + C$ 可以写成 ${(a + b)}^{2}$ 的形式，则称这三项为“完全搭配项”，若单项式 $x^{2}$ ，4和m是完全搭配项，则m可能是.（写出所有情况）

查看试题解析
19. 如图，在面积为56的长方形 $A B C D$ 中放入边长分别为6和4的正方形 $A E F G$ 和正方形 $C M N K$ ，若三块阴影部分的面积之和为16，则长方形的周长为.

查看试题解析
20. 如图，一位跑酷运动员准备以连续两次“跳跃”结束一次跑酷表演，即在水平面 $A B$ 上跑至B点，向上跃起至最高点P，然后落在点C处，继续在水平面 $C D$ 上跃起落在点D，若 $∠ A B K$ 和 $∠ K C D$ 的平分线的反向延长线刚好交于最高点P， $∠ B K C = 88 °$ ，则 $∠ P =$ 度.

查看试题解析

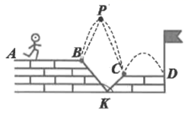
三、解答题

21. 计算：

(1)、 $x^{5} \cdot x^{10} - 2 \cdot {(x^{3})}^{5}$

(2)、 $a^{5} - {(2 a)}^{3} \times (- 2 a^{2})$

查看试题解析
22. 解方程组：

(1)、 ${\begin{array}{l} 2 x - y = 5 \\ - x - y = 2 \end{array}$

(2)、 ${\begin{array}{l} x - y = 3 (x + y) \\ 2 (x - y) + x + y = 7 \end{array}$

查看试题解析
23. 先化简，再求值： $(2 x - y) (2 x + y) - (3 x^{3} y - 12 x y^{3}) \div 3 x y$ ，其中 $x = 1, y = - 1$ .

查看试题解析
24. 某商店用41000元购买甲、乙两种服装共500件，服装的成本价与销售单价如下表所示.

类别

成本价（元/件）

销售单价（元/件）

甲

70

85

乙

90

120

(1)、该商店购买甲、乙两种服装各多少件？

(2)、若将这500件衣服全部售完，可获利多少元？

查看试题解析
25. 已知若干张正方形和长方形硬纸片如图1所示.

(1)、若用1张边长为a的正方形，2张边长为b的正方形，3张边长分别为a和b的长方形拼成一个新的长方形（如图2）.请用两种不同的方法计算图2长方形的面积并根据你的计算结果可以得到怎样的等式；

(2)、请通过拼图的方式画出一个面积为 $2 a^{2} + 5 a b + 2 b^{2}$ 的长方形示意图，并写出其因式分解的结果；

(3)、在（2）的条件下，若拼成的长方形周长为66，图1中小长方形的面积为24，则拼成的长方形面积是多少？

查看试题解析
26. 已知直线 $A B / / C D$ ，M，N分别为直线 $A B$ ， $C D$ 上的两点且 $∠ M N D = 70 °$ ，P为直线 $C D$ 上的一个动点.类似于平面镜成像，点N关于镜面 $M P$ 所成的镜像为点Q，此时 $∠ N M P = ∠ Q M P ， ∠ N P M = ∠ Q P M ， ∠ M N P = ∠ M Q P$ .

(1)、当点P在N右侧时：
①若镜像Q点刚好落在直线 $A B$ 上（如图1），判断直线 $M N$ 与直线 $P Q$ 的位置关系，并说明理由；

②若镜像Q点落在直线 $A B$ 与 $C D$ 之间（如图2），直接写出 $∠ B M Q$ 与 $∠ D P Q$ 之间的数量关系；

(2)、若镜像 $P Q ⊥ C D$ ，求 $∠ B M Q$ 的度数.

查看试题解析

落	市	担	山	七	牢	七
中	湖	为	就	吴	命	金
使	差	圾	守	立	实	华
人	忘	兴	水	分	是	心
抓	初	成	民	银	垃	距
共	青	祝	区	类	年	记
庆	找	周	和	国	州	绿

类别	成本价（元/件）	销售单价（元/件）
甲	70	85
乙	90	120

落	市	担	山	七	牢	七
中	湖	为	就	吴	命	金
使	差	圾	守	立	实	华
人	忘	兴	水	分	是	心
抓	初	成	民	银	垃	距
共	青	祝	区	类	年	记
庆	找	周	和	国	州	绿

落	市	担	山	七	牢	七
中	湖	为	就	吴	命	金
使	差	圾	守	立	实	华
人	忘	兴	水	分	是	心
抓	初	成	民	银	垃	距
共	青	祝	区	类	年	记
庆	找	周	和	国	州	绿