初中数学苏科版2020-2021学年七年级下学期期末模拟试卷
试卷更新日期:2021-06-04 类型:期末考试
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 已知a>b,则下列不等式成立的是( )
A、 a-c >b-c B、a+c<b+c C、ac>bc D、>3. 下列因式分解中,是利用提公因式法分解的是( )A、a2﹣b2=(a+b)(a﹣b) B、a2﹣2ab+b2=(a﹣b)2 C、ab+ac=a(b+c) D、a2+2ab+b2=(a+b)24. 用一根长为21厘米的铁丝围成一个三条边长均为整数厘米的等腰三角形,则方案的种数为( )A、5 B、6 C、7 D、85.如图,下列判断正确的是( )
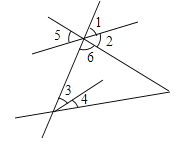 A、∠2与∠5是对顶角 B、∠2与∠4是同位角 C、∠3与∠6是同位角 D、∠5与∠3是内错角6. 下面是一名学生所做的3道练习题:①a3+a3=2a6; ②m2•m3=m6;③(2a2b)3=6a6b3 , 他做对的个数是( )A、0 B、1 C、2 D、37. 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个结论,你发现的结论是( )
A、∠2与∠5是对顶角 B、∠2与∠4是同位角 C、∠3与∠6是同位角 D、∠5与∠3是内错角6. 下面是一名学生所做的3道练习题:①a3+a3=2a6; ②m2•m3=m6;③(2a2b)3=6a6b3 , 他做对的个数是( )A、0 B、1 C、2 D、37. 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE的外部时,则∠A与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个结论,你发现的结论是( )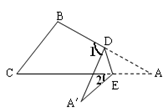 A、2∠A=∠1-∠2 B、3∠A=2(∠1-∠2) C、3∠A=2∠1-∠2 D、∠A=∠1-∠28. 小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图1;小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图2那样的正方形,中间还留下了一个洞,恰好是面积为 的小正方形,则每个小长方形的面积为( )
A、2∠A=∠1-∠2 B、3∠A=2(∠1-∠2) C、3∠A=2∠1-∠2 D、∠A=∠1-∠28. 小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图1;小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图2那样的正方形,中间还留下了一个洞,恰好是面积为 的小正方形,则每个小长方形的面积为( )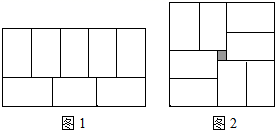 A、135cm2 B、108cm2 C、68cm2 D、60cm29. 如图所示,与∠α构成同位角的角的个数为( )
A、135cm2 B、108cm2 C、68cm2 D、60cm29. 如图所示,与∠α构成同位角的角的个数为( )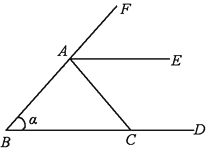 A、1 B、2 C、3 D、410. 已知 和 的方程组 的解是 ,则 和 的方程组 的解是A、 B、 C、 D、
A、1 B、2 C、3 D、410. 已知 和 的方程组 的解是 ,则 和 的方程组 的解是A、 B、 C、 D、二、填空题
-
11. 若不等式 的解集是x>3,则a的取值范围是 .12. 一根金属棒在0℃时的长度是b(m),温度每升高1℃,它就伸长a(m),当温度为x(℃)时,金属棒的长度y可用公式y=ax+b计算.已测得当x=100℃时,y=2.002m;当x=500℃时,y=2.01m.若这根金属棒加热后长度伸长到2.015m,则此时金属棒的温度是℃.13. 已知方程组 ,当m时,x+y>0.14. 某品牌电脑的成本为2400元,售价为2800元,该商店准备举行打折促销活动,要求利润率不低于5%,则这种品牌的电脑最低可打折销售.15. 已学的“幂的运算”有:①同底数幂的乘法,②幂的乘方,③积的乘方.在“(a2•a3)2=(a2)2(a3)2=a4•a6=a10”的运算过程中,运用了上述幂的运算中的(按运算顺序填序号).16. 解方程组 时,应该正确地解得 ,小明由于看错了系数c,得到的解为 则a﹣b﹣c= .17. 如图,长方形ABCD平移得到长方形A1B1C1D1 , A1B1交BC于点E,A1D1交CD于点F,若点E为BC中点,四边形A1ECF为正方形,AB=20cm,AD=10cm,则阴影部分的面积为cm2 .
 18. 如图,在△AOB和△COD中,∠AOB=∠COD=90°,∠B=50°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒20°的速度沿顺时针方向旋转一周,在旋转的过程中,在第t秒时,边CD恰好与边AB平行,则t的值为.
18. 如图,在△AOB和△COD中,∠AOB=∠COD=90°,∠B=50°,∠C=60°,点D在边OA上,将图中的△COD绕点O按每秒20°的速度沿顺时针方向旋转一周,在旋转的过程中,在第t秒时,边CD恰好与边AB平行,则t的值为.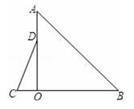
三、综合题
-
19. 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
 (1)、CD与EF平行吗?为什么?
(1)、CD与EF平行吗?为什么?
(2)、CD与EF平行吗?为什么?(3)、如果∠1=∠2,且∠3=115°,求∠ACB的度数.20. 如图,四边形ABCD中,∠BAD=106°,∠BCD=64°,点M,N分别在AB,BC上,得 FMN,若MF∥AD,FN∥DC.
求:
(1)、∠F的度数;(2)、∠D的度数.21. 已知方程组 中 为非正数, 为负数.(1)、求 的取值范围;(2)、在 的取值范围中,当 为何整数时,不等式 的解集为 ?22. 已知关于x、y的方程组 ,甲由于看错了方程①中的a , 得到方程组的解为 ;乙由于看错了方程②中的b , 得到方程组的解为 .求原方程组的正确解.23. 解关于x的不等式:ax﹣x﹣2>0.24. 为建设京西绿色走廊,改善永定河水质,某治污公司决定购买10台污水处理设备.现有A、B两种型号的设备,其中每台的价格与月处理污水量如下表:
经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
(1)、求x、y的值;(2)、如果治污公司购买污水处理设备的资金不超过105万元,求该治污公司有哪几种购买方案;(3)、在(2)的条件下,如果月处理污水量不低于2040吨,为了节约资金,请为该公司设计一种最省钱的购买方案.25. 乘法公式的探究及应用: (1)、如图,可以求出阴影部分的面积是(写成两数平方差的形式);(2)、如图,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 , 长是 , 面积是(写成多项式乘法的形式);(3)、比较左、右两图的阴影部分面积,可以得到乘法公式:(用式子表达);(4)、运用你所得到的公式,计算下列式子:(2m+n﹣p)(2m﹣n+p)26. 如图,已知 , ,求 的度数.
(1)、如图,可以求出阴影部分的面积是(写成两数平方差的形式);(2)、如图,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 , 长是 , 面积是(写成多项式乘法的形式);(3)、比较左、右两图的阴影部分面积,可以得到乘法公式:(用式子表达);(4)、运用你所得到的公式,计算下列式子:(2m+n﹣p)(2m﹣n+p)26. 如图,已知 , ,求 的度数.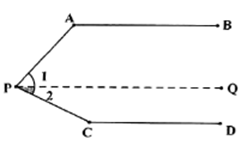 (1)、填空,在空白处填上结果或者理由.
(1)、填空,在空白处填上结果或者理由.解:过点 作 ,(如图)
得 °, ()
又因为 ,(已知)
所以 °.
因为 ,
所以 ,()
又因为 ,(已知)
所以 °,
所以 °.
(2)、请用另一种解法求 的度数.27.(1)、先观察下列等式,再完成题后问题:①请你猜想: = .
②若a、b为有理数,且 ,
求: 的值.
(2)、探究并计算:。
(3)、如图,把一个面积为1的正方形等分成两个面积为 的长方形,接着把面积为 的长方形等分成两个面积为 的正方形,再把面积为 的正方形等分成两个面积为 的矩形.如此进行下去,试利用图形揭示的规律计算: (直接写答案).