浙江省温州市乐清市八校2021年九年级学业水平第二次模拟考试数学试卷
试卷更新日期：2021-06-04 类型：中考模拟
一、 选择题(本题有10小题，每小题4分，共40分。)
-
1. 有理数2，1，-1，0中，最小的数是（ ）A、2 B、1 C、0 D、-12. 据国家卫健委数据显示，截至3月26日，各地累计报告接种新冠病毒疫苗97470000剂次，其中数据97470000用科学记数法表示为（ ）A、97.47×106 B、9.747×107 C、0.9747×108 D、9.747×1083. 如图所示的几何体，它的主视图是（ ）
A、
B、
C、
D、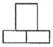
4. 一个口袋中装有3个红球，2个绿球，1个黄球，每个球除颜色外其它都相同，搅匀后随机地从中摸出一个球是绿球的概率为（ ）A、 B、 C、 D、5. 如图为某校学生到校方式统计图，若该校步行到校的学生有100人，则乘公共汽车到校的学生有（ ）学生到校方式统计图
A、80人 B、125人 C、180 人 D、200人6. 如图，在综合实践活动中，小明在学校门口的点C处测得树的顶端A仰角为37°，同时测得BC=12米，则树的高AB(单位：米)为（ ）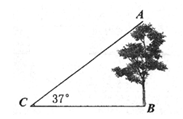
A、 B、 C、12tan37° D、12sin37°7. 某班同学到距离学校12千米的活动基地开展团日活动。一部分同学骑自行车先行，经半小时后，其余同学乘公交车出发，结果他们同时到达。已知公交车的速度是自行车速度的3倍，设自行车的速度为xkm/h，根据题意可列出方程为（ ）A、 B、 C、 D、8. 如图，PA，PB是⊙O的切线，切点分别为A，B。BC是⊙O的直径，连结AC，若AC=1，BC= ，则PA=（ ）
A、 B、2 C、 D、9. 已知两点A(-6，y1)，B(2，y2)均在抛物线y=ax2+bx+c(a>0)上，若y1>y2 ， 则抛物线的顶点横坐标m的值可以是（ ）A、-6 B、-5 C、-2 D、-110. 如图是清朝李演撰写的《仇章算术细草图说》中的“勾股圆方图”，四边形ABCD，四边形EBGF，四边形HNQD均为正方形，BG，NQ，BC是某个直角三角形的三边，其中BC是斜边，若HM：EM=8：9，HD=2，则AB的长为（ ）
A、 B、 C、3 D、二、填空题(本题有6小题，每小题5分，共30分)
-
11. 因式分解： m2-16=12. 若一元二次方程x2-6x+c=0有两个相等的实数根，则c=13. 一个圆锥的底面半径r=6，母线l=10，则这个圆锥的侧面积是14. 如图，一次函数y= x+3的图象与x轴，y轴分别交于A，B两点.C是线段AB上一点，CD⊥OA于点D，CE⊥OB于点E，OD=2OE，则点C的坐标为
15. 如图，A是双曲线y= (k>0，x>0)上一点，B是x轴正半轴上一点，以AB为直角边向右构造等腰直角三角形ABC，∠BAC=90°，过点A作AD⊥y轴于点D，以AD为斜边向上构造等腰直角三角形ADE，若点C，点E恰好都落在该双曲线上，△ABC与△ADE的面积之和为28，则k=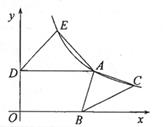
16. 图1是某个零件横截面的示意图，已知AB=CD，∠B=∠C，为了求出BC的长度，小王将宽度为2cm的直尺按图2、图3、图4的三种方式摆放，所测得的具体数据(单位：cm)如图所示，则AB=cm，BC=cm。
三、解答题(本题有8小题，共80分)
-
17.(1)、计算：|-3|+(1- )0- -(-2)(2)、化简：(a-3)2-a(a+8)18. 如图，AD，BC相交于点O，OA=OB，∠C=∠D=90°
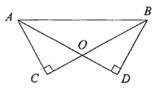(1)、求证：△ACB≌△BDA(2)、当AC=3，AB=5时，求OD的长19. 某公司销售部有营销人员15人，为了对达到或者超出月销售定额的员工进行表彰，统计了这15人某月的销售量(单位：件)如下：每人销售件数
1400
880
270
150
130
120
人数
1
1
3
6
3
1
(1)、求这15位营销人员该月销售量的平均数；
(2)、假设销售负贵人把月销售定额定为280件，你认为是否合理，为什么？如不合理，请你制定一个较合理的销售定额，并说明理由。20. 如图，在7×5的方格纸中，每个小正方形的边长为1，△ABC的顶点A，B，C均落在格点上，请利用-把无刻度直尺作图，并保留作图痕迹．
(1)、在图1中画出BC边上的中线AD。(2)、在图2中，E是线段AB上一点，AE= 。画出一个四边形AECF (点F在网格线上)，使这个四边形为平行四边形。21. 在平面直角坐标系中，已知点A(4，-1)，B(4，3)，C(6，5)，抛物线y=ax2+bx-1恰好经过A，B，C三点中的两点。(1)、求抛物线的函数表达式。(2)、D是射线AB上一点，过点D作x轴的平行线交抛物线于点E(m，y1)，F(n，y1)，点E在F的左边。若m+n=4FD，求点E的坐标。22. 如图，AB是⊙O的直径，弦CD⊥AB于点H，G是 上一点，连结BC，AG，GD。AG分别交CD，BC于点E，F。已知AE=CE。
(1)、求证：C是 的中点。(2)、若AB=13，tanD= ，求DG的长。23. 目前我国新冠病毒疫情有很大好转，但是防疫不能放松，某物业公司向超市购买A、B、C三种型号的消毒湿巾分别分给第一周、第二周、第三周工作的员工使用，每人每周1包，这三周员工人数之和为100人已知购买1包A型湿巾和2包B型湿巾共需要130元购买2包A型湿巾和3包B型湿巾共需要220元，已知C型湿巾每包10元，第一周员工人数<第二周员工人数<第三周员工人数。(1)、求A型湿巾和B型湿巾的单价。(2)、该超市促销方案如下：每购买1包A型湿巾则赠送2包C型湿巾。①若公司购买了第-周所需的A型湿巾后，赠送的C型湿巾刚好够第三周使用，求物业公司购买三种湿巾所需总金额的最小值。
②若第三周需要的C型湿巾除了赠送外，还需另外购买，最终三种湿巾总共花费了2560元，求所有满足要求的购买方案。
24. 如图，在菱形ABCD中，已知AB=6，∠ABC=60°，点E，点F分别在AD与CD的延长线上，连结EF，DE=DF，连结BF交AD于点N，H是BF的中点，连结CH并延长交AD于点M，交BA的延长线于点G。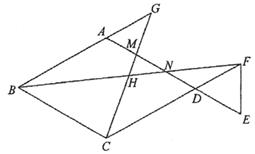
(1)、求证：AG=DF。(2)、若DE=3。①求AM与BN的值。
②点P是线段BN或线段CM上一点，当△PMN是以MN为腰的等腰三角形时，求所有满足条件的PH的值。
(3)、连结AC，HE，将点M绕着点H旋转60°得到点K，当点K恰好落在AC上时，求△KHC与△MHE的面积之比。