浙江省丽水市庆元县2021年数学中考二模试卷
试卷更新日期:2021-06-04 类型:中考模拟
一、选择题(本题有10 小题,每小题3分,共30分.)
-
1. 实数0,1,-3,-1中最大的数是( )A、0 B、1 C、-3 D、-12. 据统计局发布,2020年市粮食播种面积约为7300000公顷,数据7300000用科学记数法表示为( )A、7.3×106 B、7.3×107 C、0.73×106 D、0.73×1073. 代数式 有意义,则x的取值可以为( )A、-2 B、-1 C、1 D、24. 如图,已知图形X和直线l,以直线l为对称轴,图形X的轴对称图形是( )
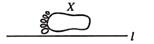 A、
A、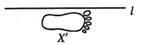 B、
B、 C、
C、 D、
D、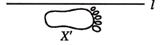 5. 某小组5名同学在一周内参加家务劳动的时间如下表所示,关于“劳动时间”的这组数据,以下说法正确的是( )
5. 某小组5名同学在一周内参加家务劳动的时间如下表所示,关于“劳动时间”的这组数据,以下说法正确的是( )劳动时间(小时)
3
3.5
4
4.5
人数
1
1
2
1
A、众数是4.5 B、中位数是4 C、极差是0.5 D、平均数是3.756. 《九章算术》中记载一问题:今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?意思是:今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又差4钱。问人数、物价各多少?设有x人,则表示物价的代数式可以是( )A、8x-3 B、8x+3 C、7x-4 D、7(x+4)7. 如图,在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,测出每一次加压后汽缸内气体的体积V和气体对汽缸壁所产生的压强p。根据"下表中的数据规律进行探求,当汽缸内气体的体积压缩到70mL时压力表读出的压强值a最接近( )体积V 压强p(kPa) 100 60 90 67 80 75 70 a 60 100
 A、80kPa B、85kPa C、90kPa D、100 kPa8. 如图,△ABC内接于⊙O,其外角∠BAE的平分线交⊙O于点D,点A为弧CD的中点。若∠ABC=28°,则∠ACB的大小为( )
A、80kPa B、85kPa C、90kPa D、100 kPa8. 如图,△ABC内接于⊙O,其外角∠BAE的平分线交⊙O于点D,点A为弧CD的中点。若∠ABC=28°,则∠ACB的大小为( ) A、84° B、85° C、86° D、88°9. 按图示的方法,搭1个正方形需要4根火柴棒,搭3个正方形需要10根火柴棒,搭6个正方形需要18根火柴棒,则下列选项中,可以搭成符合规律图形的火柴棒的数目是( )
A、84° B、85° C、86° D、88°9. 按图示的方法,搭1个正方形需要4根火柴棒,搭3个正方形需要10根火柴棒,搭6个正方形需要18根火柴棒,则下列选项中,可以搭成符合规律图形的火柴棒的数目是( )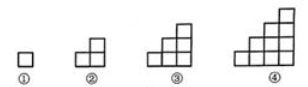 A、52根 B、66根 C、70根 D、72根10. 如图,在正方形ABCD中,点E,F,G分别在边BC,CD,DA上,四边形EFGH由两个正方形组成,且AB=1,则线段BE的长为( )
A、52根 B、66根 C、70根 D、72根10. 如图,在正方形ABCD中,点E,F,G分别在边BC,CD,DA上,四边形EFGH由两个正方形组成,且AB=1,则线段BE的长为( ) A、 -1 B、3- C、 D、
A、 -1 B、3- C、 D、二、填空题(本题有6小题,每小题4分,共24分)
-
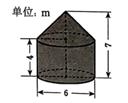
11. 因式分解:x2-4=12. 一个不透明的盒子中装有3个红球,2个黄球,这些球除了颜色外无其他差别,从中随机摸出一个小球,则摸到黄球的概率为13. 如图,粮仓由简仓(圆柱)和仓顶(圆锥)组合而成,则该粮仓仓顶的表面积为m2(结果保留π)
 14. 如图,四边形ABCD中,∠ABC=∠CDA=90°,分别以它的四条边为斜边,向外作等腰直角三角形,其中3个三角形面积分别为2,5,9,则第4个三角形面积为
14. 如图,四边形ABCD中,∠ABC=∠CDA=90°,分别以它的四条边为斜边,向外作等腰直角三角形,其中3个三角形面积分别为2,5,9,则第4个三角形面积为 15. 如图,在平面直角坐标系中,AB=AC=5,点B和点C的坐标分别为(-2,0),(4,0),反比例函数y= (x>0)的图象经过点A,且与AC相交于另一点D,作AE⊥BC于点E,交BD于点F,则点F的坐标为
15. 如图,在平面直角坐标系中,AB=AC=5,点B和点C的坐标分别为(-2,0),(4,0),反比例函数y= (x>0)的图象经过点A,且与AC相交于另一点D,作AE⊥BC于点E,交BD于点F,则点F的坐标为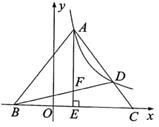 16. 如图1是一款铲车模型,其起物装置由悬臂与大铲斗所组成,图2是其简化示意图铲斗AB长1米,离地面高度为0.25米,前悬臂BC长为2米,后悬臂CD长为2米,前悬臂与后悬臂张角为α(α不超过120)起物开始状态时AB∥CD,∠BCD=120°,在起物过程中,铲斗始终与地面平行,后悬臂CD的旋转角为β(β不超过90°)
16. 如图1是一款铲车模型,其起物装置由悬臂与大铲斗所组成,图2是其简化示意图铲斗AB长1米,离地面高度为0.25米,前悬臂BC长为2米,后悬臂CD长为2米,前悬臂与后悬臂张角为α(α不超过120)起物开始状态时AB∥CD,∠BCD=120°,在起物过程中,铲斗始终与地面平行,后悬臂CD的旋转角为β(β不超过90°) (1)、铲斗离地面的最大高度为米(2)、铲斗最外端点A离点D的最远距离为米
(1)、铲斗离地面的最大高度为米(2)、铲斗最外端点A离点D的最远距离为米三、解答题(本题有8小题,共66分。)
-
17. 计算:| |+2-1+ -2sin45°18. 先化简,再求值: ,其中a= .19. 某中学为了普及疫情防控知识,校团委就本校学生对疫情防控知识进行了一次测试。经过对测试成绩的分析,得到如下图所示的两幅不完整的统计图(A:59分及以下;B:60--69分;C:70--79分;D:80--89分;E:90--100分)(得分均为整数).
请你根据图中提供的信息解答以下问题:
 (1)、求该校共有多少名学生;(2)、将条形统计图补充完整;(3)、在扇形统计图中,计算出“60--69分”部分所对应的圆心角的度数。20. 如图,AB是⊙O的直径,⊙O过AC的中点D,DE切⊙O于点D,交BC于点E。
(1)、求该校共有多少名学生;(2)、将条形统计图补充完整;(3)、在扇形统计图中,计算出“60--69分”部分所对应的圆心角的度数。20. 如图,AB是⊙O的直径,⊙O过AC的中点D,DE切⊙O于点D,交BC于点E。 (1)、求证:DE⊥BC(2)、若⊙O的半径为5,BE=2,求DE的长度。21. 甲,乙两人沿同-条公路从A地出发到B地,甲骑自行车,乙骑摩托车,甲比乙先出发。已知A,B两地相距120km,如图表示的是两人之间相距的路程s(km)与甲行驶的时间t(h)之间函数关系的部分图象。请解答下列问题:
(1)、求证:DE⊥BC(2)、若⊙O的半径为5,BE=2,求DE的长度。21. 甲,乙两人沿同-条公路从A地出发到B地,甲骑自行车,乙骑摩托车,甲比乙先出发。已知A,B两地相距120km,如图表示的是两人之间相距的路程s(km)与甲行驶的时间t(h)之间函数关系的部分图象。请解答下列问题: (1)、写出点C纵坐标的实际意义。(2)、求甲,乙的速度。(3)、请将图象补充完整,并直接写出关键点的坐标。22. 已知二次函数y=-(x-m)2+m(1)、写出该函数图象顶点的坐标及其所在直线的函数表达式。(2)、若该函数图象的顶点在第一象限,试判断该函数图象与x轴的交点个数并说明理由。(3)、若在-2≤x≤2范围内,若图象上的点到x轴的距离最小值为2,求m的值。23. [实验操作]如图1是一张矩形纸片,点E在边AB上,把△BCE沿着直线CE对折,点B恰好落在对角线AC上的点F处。
(1)、写出点C纵坐标的实际意义。(2)、求甲,乙的速度。(3)、请将图象补充完整,并直接写出关键点的坐标。22. 已知二次函数y=-(x-m)2+m(1)、写出该函数图象顶点的坐标及其所在直线的函数表达式。(2)、若该函数图象的顶点在第一象限,试判断该函数图象与x轴的交点个数并说明理由。(3)、若在-2≤x≤2范围内,若图象上的点到x轴的距离最小值为2,求m的值。23. [实验操作]如图1是一张矩形纸片,点E在边AB上,把△BCE沿着直线CE对折,点B恰好落在对角线AC上的点F处。
[性质探究]如图2,连结DF,若点E,F,D在同一直线上。
 (1)、请写出图中与边DC相等的线段并说明理由。(2)、若AE=2,求EF的长。(3)、[迁移应用]
(1)、请写出图中与边DC相等的线段并说明理由。(2)、若AE=2,求EF的长。(3)、[迁移应用]
如图3,延长EF交边AD于点G,若DG:AG=n,且AE=2,求BE的长(请用含n的代数式来表示) 24. 如图,在四边形ABCD中,AD∥BC,BA=AD=DC=2,∠ABC=45°,E是BC边上一动点,连结AE,将AE绕点A逆时针旋转135°到AF,连结EF与AD交于点G,连结DE,DF,设BE的长为x。
24. 如图,在四边形ABCD中,AD∥BC,BA=AD=DC=2,∠ABC=45°,E是BC边上一动点,连结AE,将AE绕点A逆时针旋转135°到AF,连结EF与AD交于点G,连结DE,DF,设BE的长为x。 (1)、求证:△ABE≌△ADF(2)、若△DEF的面积为y,求y关于x的函数表达式,并求y的最大值。(3)、当△FGD是等腰三角形时,求x的值。
(1)、求证:△ABE≌△ADF(2)、若△DEF的面积为y,求y关于x的函数表达式,并求y的最大值。(3)、当△FGD是等腰三角形时,求x的值。