广西北部湾经济区2021年中考全真模拟考试数学试卷(四)
试卷更新日期:2021-06-04 类型:中考模拟
一、选择题(共12小题,每小题3分,共36分。)
-
1. 在下列四个实数中,最大的数是( )A、-3 B、0 C、2 D、32. 下列图形中,是轴对称图形但不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 在平面直角坐标系中,点A(a,2)在第二象限内,则a的取值可以是( )A、-1 B、2 C、3 D、4或-44. 下列计算 正确的是( )A、2a+3b=5ab B、a3·a2=a5 C、(-a2)3=a6 D、(a+b)2=a2+b25.
3. 在平面直角坐标系中,点A(a,2)在第二象限内,则a的取值可以是( )A、-1 B、2 C、3 D、4或-44. 下列计算 正确的是( )A、2a+3b=5ab B、a3·a2=a5 C、(-a2)3=a6 D、(a+b)2=a2+b25.已知:菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=6cm,则OE的长为( )
 A、6cm B、4cm C、3cm D、2cm6. 如果A(-2,n),B(2,n),C(4,n+12)这三个点都在同一个函数的图象上,那么这个函数的解析式可能是( )A、y=2x B、y= C、y=-x2 D、y=x27. 已知一组数据5,6,7,8,9,5,9,若增加一个数7,则新的这组数据与原来相比( )A、平均数变大,方差变大 B、平均数不变,方差变大 C、平均数不变,方差变小 D、平均数不变,方差不变8. 若关于x的一元二次方程ax2-2x+1=0有两个实数根,则实数a的取值范围是( )A、a≤1且a≠0 B、a<1且a≠0 C、a≤1 D、a<19. 某同学从家骑自行车上学,先上坡到达A地后再下坡到达学校,所用的时间与行驶的路程如图所示,如果返程上、下坡速度保持不变,那么他从学校回到家需要的时间是( )
A、6cm B、4cm C、3cm D、2cm6. 如果A(-2,n),B(2,n),C(4,n+12)这三个点都在同一个函数的图象上,那么这个函数的解析式可能是( )A、y=2x B、y= C、y=-x2 D、y=x27. 已知一组数据5,6,7,8,9,5,9,若增加一个数7,则新的这组数据与原来相比( )A、平均数变大,方差变大 B、平均数不变,方差变大 C、平均数不变,方差变小 D、平均数不变,方差不变8. 若关于x的一元二次方程ax2-2x+1=0有两个实数根,则实数a的取值范围是( )A、a≤1且a≠0 B、a<1且a≠0 C、a≤1 D、a<19. 某同学从家骑自行车上学,先上坡到达A地后再下坡到达学校,所用的时间与行驶的路程如图所示,如果返程上、下坡速度保持不变,那么他从学校回到家需要的时间是( ) A、7分钟 B、9分钟 C、12分钟 D、14分钟10. 如图,在矩形ABCD中,AB=2,BC=2 ,E是BC的中点,将△ABE沿直线AE翻折,点B落在点F处,连接CF,则cos∠ECF的值为( )
A、7分钟 B、9分钟 C、12分钟 D、14分钟10. 如图,在矩形ABCD中,AB=2,BC=2 ,E是BC的中点,将△ABE沿直线AE翻折,点B落在点F处,连接CF,则cos∠ECF的值为( )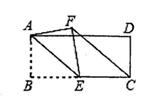 A、 B、 C、 D、11. 将关于x的一元二次方程x2-px+q=0变形为x2=px-q,就可以将x2表示为关于x的一次多项式,从而达到“降次”的目的,又如x3=x·x2=x(px-q)=……,我们将这种方法称为“降次法”,通过这种方法可以化简次数较高的代数式。根据“降次法”,已知:x2-x-1=0,且x>0,则x4-2x3+3x的值为( )A、1- B、3 C、1+ D、3+12. 如图,在平面直角坐标系中,点A的坐标为 , 轴于点B,点C是线段 上的点,连结 .点P在线段 上,且 .函数 的图象经过点P.当点C在线段 上运动时,k的取值范围是( )
A、 B、 C、 D、11. 将关于x的一元二次方程x2-px+q=0变形为x2=px-q,就可以将x2表示为关于x的一次多项式,从而达到“降次”的目的,又如x3=x·x2=x(px-q)=……,我们将这种方法称为“降次法”,通过这种方法可以化简次数较高的代数式。根据“降次法”,已知:x2-x-1=0,且x>0,则x4-2x3+3x的值为( )A、1- B、3 C、1+ D、3+12. 如图,在平面直角坐标系中,点A的坐标为 , 轴于点B,点C是线段 上的点,连结 .点P在线段 上,且 .函数 的图象经过点P.当点C在线段 上运动时,k的取值范围是( )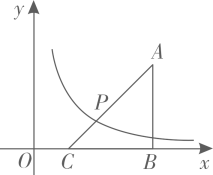 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本小题共6小题,每小题3分,共18分)
-
13. 在函数y= 中,自变量x的取值范围是。14. 在△ABC中,∠C=90°,tanA= ,则cosB=。15. 如果把抛物线y=2x2-1向左平移1个单位,同时向上平移4个单位,那么得到的新的抛物线是。16. 如图,为测量平地上一块不规则区域(图中的阴影部分)的面积,画一个边长为2m的正方形,使不规则区域落在正方形内,现向正方形内随机投掷小石子(假设小石子落在正方形内每一点都是等可能的),经过大量重复投掷试验,发现小石子落在不规则区域的频率稳定在常数0.25附近,由此可估计不规则区域的面积是 m2 .
 17. 如图,正方形 的边长为1,将其绕顶点C按逆时针方向旋转一定角度到 位置,使得点B落在对角线 上,则阴影部分的面积是 .
17. 如图,正方形 的边长为1,将其绕顶点C按逆时针方向旋转一定角度到 位置,使得点B落在对角线 上,则阴影部分的面积是 . 18. 如图,在△ABC中,∠A=90°,∠B=60°,AB=2,若D是BC上一动点,则2AD+DC的最小值为 。
18. 如图,在△ABC中,∠A=90°,∠B=60°,AB=2,若D是BC上一动点,则2AD+DC的最小值为 。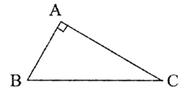
三、解答题(本大题共8小题,共66分.)
-
19. 计算:(π-5)0+ ×cos45°-|-3|+( )-220. 解方程:21. 在8×5的网格中建立如图的平面直角坐标系,四边形OABC的顶点坐标分别为0(0,0),A(3,4),B(8,4),C(5,0)。仅用无刻度的直尺在给定网格中按下列步骤完成画图,并回答问题:
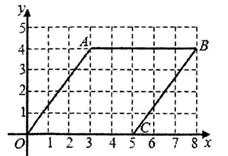
( 1 )将线段CB绕点C逆时针旋转90°,画出对应线段CD;
( 2 )在线段AB上画点E,使∠BCE=45°(保留画图过程的痕迹);
( 3 )连接AC,画点E关于直线AC的对称点F,并简要说明画法。
22. 莫菲、隆迪、紫惠和曲代4人一起去火锅店吃火锅,4人在如图所示的四人桌前就座,其中莫菲和紫惠坐在餐桌的同侧。 (1)、请用适当的方法表示出所有的不同就座方案。(2)、请问隆迪恰好坐在靠近过道一侧的概率是多少?23. 古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的是圆”。请研究如下美丽的圆,如图,线段AB是⊙O的直径,延长AB至点C,使BC=OB,点E是线段OB的中点,DE⊥AB交⊙O于点D,点P是⊙O上一动点(不与点A,B重合),连接CD,PE,PC。
(1)、请用适当的方法表示出所有的不同就座方案。(2)、请问隆迪恰好坐在靠近过道一侧的概率是多少?23. 古希腊数学家毕达哥拉斯认为:“一切平面图形中最美的是圆”。请研究如下美丽的圆,如图,线段AB是⊙O的直径,延长AB至点C,使BC=OB,点E是线段OB的中点,DE⊥AB交⊙O于点D,点P是⊙O上一动点(不与点A,B重合),连接CD,PE,PC。 (1)、求证:CD是⊙O的切线;(2)、小明在研究的过程中发现 是一个确定的值,回答这个确定的值是多少?并对小明发现的结论加以证明。24. 为响应“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成。设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图)。
(1)、求证:CD是⊙O的切线;(2)、小明在研究的过程中发现 是一个确定的值,回答这个确定的值是多少?并对小明发现的结论加以证明。24. 为响应“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成。设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图)。 (1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、若矩形空地的面积为160m2 , 求x的值;(3)、若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由。
(1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、若矩形空地的面积为160m2 , 求x的值;(3)、若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由。甲
乙
丙
单价(元/棵)
14
16
28
合理用地(m2/棵)
0.4
1
0.4
25. 如图,抛物线y=ax2+bx+c经过A(-1,0)、B(4,0)、C(0,2)三点,点D(x,y)为抛物线上第一象限内的一个动点。 (1)、求抛物线所对应的函数表达式;(2)、当△BCD的面积为3时,求点D的坐标;(3)、过点D作DE⊥BC,垂足为点E,是否存在点D,使得△CDE中的某个角等于∠ABC的2倍?若存在,求点D的横坐标;若不存在,请说明理由。26. 综合与实践
(1)、求抛物线所对应的函数表达式;(2)、当△BCD的面积为3时,求点D的坐标;(3)、过点D作DE⊥BC,垂足为点E,是否存在点D,使得△CDE中的某个角等于∠ABC的2倍?若存在,求点D的横坐标;若不存在,请说明理由。26. 综合与实践 (1)、[问题发现]如图1,△ABC和△ADE均为等边三角形,点B,D,E在同一条直线上。填
(1)、[问题发现]如图1,△ABC和△ADE均为等边三角形,点B,D,E在同一条直线上。填空:①线段BD,CE之间的数量关系为;②∠BEC=°。
(2)、[类比探究]如图2,△ABC和△ADE均为等腰直角三角形,∠ACB=∠AED= 90°,AC=BC,AE=DE,点B,D,E在同一条直线上,请判断线段BD,CE之间的数量关系及∠BEC的度数,并给出证明。(3)、如图3,在△ABC中,∠ACB=90°,∠A=30°,AB=5,点D在AB边上,DE⊥AC于点E,AE=3,将△ADE绕点A旋转,当DE所在直线经过点B时,CE的长是多少?(直接写出答案)