广西北部湾经济区2021年中考全真模拟考试数学试卷(三)
试卷更新日期:2021-06-04 类型:中考模拟
一、选择题(共12小题,每小题3分,共36分。)
-
1. 中国古代数学著作《九章算术》中,在世界数学史上首次正式引入负数。如果温度上升2℃记作+2℃,那么温度下降3℃记作( )A、+2℃ B、-2℃ C、+3℃ D、-3℃2. 一个几何体的三视图如图所示,则这个几何体可能是( )
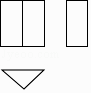 A、
A、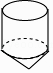 B、
B、 C、
C、 D、
D、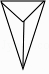 3. 我国的“嫦娥五号”于2020年11月24日成功发射,它会将采集的月球样品带回国内,为人类宇宙开拓之路添上重要一笔,月球距离地球的平均距离为384000千米,数据384000用科学记数法表示为( )A、384×103 B、38.4×104 C、3.84×105 D、0.384×1064. 下列运算正确的是( )A、2a+3b=5ab B、a5÷a=a4(a≠0) C、(2a)3=6a3 D、a2·a3=a65. 以下调查中,不适合采用全面调查方式的是( )A、了解全班同学健康码的情况 B、了解我国全体中小学生对“冠状病毒”的知晓程度 C、为准备开学,对全班同学进行每日温度测量统计 D、“新型冠状病毒”疫情期间,对所有疑似病例病人进行核酸检测6. 已知 ABCD,根据图中尺规作图的痕迹,判断下列结论中不一定成立的是( )
3. 我国的“嫦娥五号”于2020年11月24日成功发射,它会将采集的月球样品带回国内,为人类宇宙开拓之路添上重要一笔,月球距离地球的平均距离为384000千米,数据384000用科学记数法表示为( )A、384×103 B、38.4×104 C、3.84×105 D、0.384×1064. 下列运算正确的是( )A、2a+3b=5ab B、a5÷a=a4(a≠0) C、(2a)3=6a3 D、a2·a3=a65. 以下调查中,不适合采用全面调查方式的是( )A、了解全班同学健康码的情况 B、了解我国全体中小学生对“冠状病毒”的知晓程度 C、为准备开学,对全班同学进行每日温度测量统计 D、“新型冠状病毒”疫情期间,对所有疑似病例病人进行核酸检测6. 已知 ABCD,根据图中尺规作图的痕迹,判断下列结论中不一定成立的是( ) A、DE=BE B、∠DEA= ∠DAB C、∠DEA=∠BAE D、AD= DE7. 关于x的一元二次方程x2-mx+m-2=0的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、m不确定,所以无法判断8. 袋中装有6个黑球和n个白球,经过若干次试验,发现“若从袋中任摸出一个球,恰是黑球的概率为 ,则这个袋中白球大约有多少个( )A、16 B、10 C、12 D、89. 某厂家2020年1~5月份的口罩产量统计如图所示。设从2月份到4月份,该厂家口罩产量的平均月增长率为x,根据题意可得方程( )
A、DE=BE B、∠DEA= ∠DAB C、∠DEA=∠BAE D、AD= DE7. 关于x的一元二次方程x2-mx+m-2=0的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、m不确定,所以无法判断8. 袋中装有6个黑球和n个白球,经过若干次试验,发现“若从袋中任摸出一个球,恰是黑球的概率为 ,则这个袋中白球大约有多少个( )A、16 B、10 C、12 D、89. 某厂家2020年1~5月份的口罩产量统计如图所示。设从2月份到4月份,该厂家口罩产量的平均月增长率为x,根据题意可得方程( ) A、180(1-x)2=461 B、368(1-x)2=442 C、180(1+x)2=461 D、368(1+x)2=44210. 勾股定理是人类最伟大的科学发现之一,在我国古代《周髀算经》中早有记载。如图①,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图②的方式放置在最大正方形内。若图中阴影部分图形的面积为3,则较小两个正方形重叠部分图形的面积为( )
A、180(1-x)2=461 B、368(1-x)2=442 C、180(1+x)2=461 D、368(1+x)2=44210. 勾股定理是人类最伟大的科学发现之一,在我国古代《周髀算经》中早有记载。如图①,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图②的方式放置在最大正方形内。若图中阴影部分图形的面积为3,则较小两个正方形重叠部分图形的面积为( ) A、1 B、2 C、3 D、411. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G,若EF=EG,则CD的长为( )
A、1 B、2 C、3 D、411. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G,若EF=EG,则CD的长为( )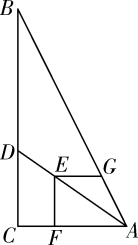 A、3.6 B、4 C、4.8 D、512. 如图,在平面直角坐标系中,Q是直线y= x+2上的一个动点,将Q绕点P(1,0)顺时针旋转90°,得到点Q',连接OQ',则OQ'的最小值为( )
A、3.6 B、4 C、4.8 D、512. 如图,在平面直角坐标系中,Q是直线y= x+2上的一个动点,将Q绕点P(1,0)顺时针旋转90°,得到点Q',连接OQ',则OQ'的最小值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本小题共6小题,每小题3分,共18分)
-
13. 在函数y= 中,自变量x的取值范围是 .14. 因式分解:8a3-2ab2=。15. 某招聘考试分笔试和面试两部分,其中笔试按70%、面试按30%计算加权平均数作为总成绩。小明笔试成绩为90分,面试成绩为80分,那么小明的总成绩为分。16. 如图,在数学活动课中,小敏为了测量校园内旗杆AB的高度.站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.若旗杆与教学楼的距离为9m,则旗杆AB的高度是 m(结果保留根号)
 17. 如图,在平面直角坐标系中,矩形ABCD的顶点A,C分别在x轴,y轴的正半轴上,点D(-2,3),AD=5,若反比例函数y= (k>0,x>0)的图象经过点B,则k的值为。
17. 如图,在平面直角坐标系中,矩形ABCD的顶点A,C分别在x轴,y轴的正半轴上,点D(-2,3),AD=5,若反比例函数y= (k>0,x>0)的图象经过点B,则k的值为。 18. 如图,四边形ABCD,对角线AC,BD交于点E,AC= BD,∠AEB=60°,∠ABD+∠ACD=180°,AB=3,AC=7,则线段CD的长为。
18. 如图,四边形ABCD,对角线AC,BD交于点E,AC= BD,∠AEB=60°,∠ABD+∠ACD=180°,AB=3,AC=7,则线段CD的长为。
三、解答题(本大题共8小题,共66分.)
-
19. 计算:4sin30°+( )-1-20210-20. 先化简,再求值: ,其中 .21. 如图,在由边长为1个单位长度的小正方形组成的10×10网格中,已知点O,A,B均为网格线的交点。
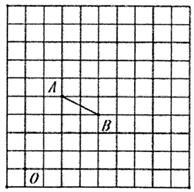
( 1 )在给定的网格中,以点O为位似中心,将线段AB放大为原来的2倍,得到线段A1B1(点A,B的对应点分别为A1 , B1)。画出线段A1B1;
( 2 )将线段A1B1绕点B1逆时针旋转90°得到线段A2B1 , 画出线段A2B1;
( 3 )求以A,A1 , B1 , A2为顶点的四边形AA1B1A2的面积。
22. 某社区为了加强居民对新型冠状病毒肺炎防护知识的了解,鼓励社区居民在线参与《2020年新型冠状病毒防护知识问卷(满分100分》作答,社区管理员随机从甲、乙两个小区各抽取20人的答卷成绩(单位:分)进行统计、分析,过程如下:收集数据:
甲小区:85 80 95 100 90 95 85 65 75 85 90 90 70 90 100 80 80 90 95 75
乙小区:80 95 80 95 65 100 100 85 85 80 95 75 80 90 70 80 95 75 100 90
整理数据:
成绩x(分)
60≤x≤70
70≤x≤80
80≤x≤90
90≤x≤100
甲小区
a
5
b
5
乙小区
2
7
5
6
分析数据:
统计量
平均数
中位数
众数
甲小区
85.75
85.75
c
乙小区
85.75
85
80
应用数据:
(1)、填空:a= , b= , c=。(2)、若甲小区共有800人参与答卷,请估计甲小区成绩大于90分的人数;(3)、根据数据统计,你认为哪个小区对新型冠状病毒肺炎防护知识掌握更好,请写出你判断的理由。23. 如图,⊙O是△ABC的外接圆,∠BAC的平分线交⊙O于点D,交BC于点E,过D作直线DF∥BC,连接BD。 (1)、求证:DF是⊙O的切线;(2)、若AB=8,AE=6,CE=3,求BD的长。24. 突如其来的新冠疫情影响了某厂经济效益,在复工复产对产品价格进行了调整,每件的售价比进价多8元,8件的进价相当于6件的售价,每天可售出200件,经市场调查发现,如果每件商品涨价1元,每天就会少卖5件。(1)、该商品的售价和进价分别是多少元?(2)、在进价不变的条件下,若每天所得的销售利润为2035元时,且销量尽可能大,该商品应涨价多少元?(3)、在进价不变的条件下,商场的营销部在调控价格方面,提出了A,B两种营销方案:方案A:每件商品涨价不超过15元;方案B:每件商品的利润至少为26元.请比较哪种方案的利润更大,并说明理由.25. 如图,抛物线y=ax2+bx+ 8(a≠0)与x轴交于点A(-2,0)和点B(8,0),与y轴交于点C,顶点为D,连接AC,BC,BC与抛物线的对称轴l交于点E。
(1)、求证:DF是⊙O的切线;(2)、若AB=8,AE=6,CE=3,求BD的长。24. 突如其来的新冠疫情影响了某厂经济效益,在复工复产对产品价格进行了调整,每件的售价比进价多8元,8件的进价相当于6件的售价,每天可售出200件,经市场调查发现,如果每件商品涨价1元,每天就会少卖5件。(1)、该商品的售价和进价分别是多少元?(2)、在进价不变的条件下,若每天所得的销售利润为2035元时,且销量尽可能大,该商品应涨价多少元?(3)、在进价不变的条件下,商场的营销部在调控价格方面,提出了A,B两种营销方案:方案A:每件商品涨价不超过15元;方案B:每件商品的利润至少为26元.请比较哪种方案的利润更大,并说明理由.25. 如图,抛物线y=ax2+bx+ 8(a≠0)与x轴交于点A(-2,0)和点B(8,0),与y轴交于点C,顶点为D,连接AC,BC,BC与抛物线的对称轴l交于点E。 (1)、求抛物线的表达式;(2)、点P是第一象限内拋物线上的动点,连接PB,PC,当S△PBC= S△ABC时,求点P的坐标;(3)、点N是对称轴l右侧抛物线上的动点,在射线ED上是否存在点M,使得以点M,N,E为顶点的三角形与△OBC相似?若存在,求点M的坐标;若不存在,请说明理由。26. 对于平面直角坐标系xOy中的点P(a,b),若点P'的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P"为点P的“k属派生点”。例如:P(1,4)的“2属派生点”为P(1+2×4,2×1+4),即P(9,6)。
(1)、求抛物线的表达式;(2)、点P是第一象限内拋物线上的动点,连接PB,PC,当S△PBC= S△ABC时,求点P的坐标;(3)、点N是对称轴l右侧抛物线上的动点,在射线ED上是否存在点M,使得以点M,N,E为顶点的三角形与△OBC相似?若存在,求点M的坐标;若不存在,请说明理由。26. 对于平面直角坐标系xOy中的点P(a,b),若点P'的坐标为(a+kb,ka+b)(其中k为常数,且k≠0),则称点P"为点P的“k属派生点”。例如:P(1,4)的“2属派生点”为P(1+2×4,2×1+4),即P(9,6)。 (1)、若点P的“3属派生点”P"的坐标为(6,2),求点P的坐标;(2)、若点P在x轴的正半轴上,点P的“k属派生点”为P"点,且线段PP'的长度为线段OP长度的2倍,求k的值;(3)、如图,已知点A(0,2),点P是x轴上一点,且是点(2,4)的“属派生点”,以线段AP为一边,在其一侧作如图所示等边三角线APQ.现P点沿x轴运动,当点P运动到原点O处时,记Q的位置为B。问三角形ABQ的面积是否是一个定值,如果是,请求出面积;如果不是,请说明理由。
(1)、若点P的“3属派生点”P"的坐标为(6,2),求点P的坐标;(2)、若点P在x轴的正半轴上,点P的“k属派生点”为P"点,且线段PP'的长度为线段OP长度的2倍,求k的值;(3)、如图,已知点A(0,2),点P是x轴上一点,且是点(2,4)的“属派生点”,以线段AP为一边,在其一侧作如图所示等边三角线APQ.现P点沿x轴运动,当点P运动到原点O处时,记Q的位置为B。问三角形ABQ的面积是否是一个定值,如果是,请求出面积;如果不是,请说明理由。