河南省许昌长葛市2021年数学中招一模试卷

试卷更新日期：2021-06-04 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算 $\sin 30 °$ 的值等于（）

A、 $\sqrt{3}$ B、 $\frac{1}{2}$ C、 $\frac{\sqrt{2}}{3}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
2. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列说法中正确的是（　　）

A、掷两枚质地均匀的硬币，“两枚硬币都是正面朝上”这一事件发生的概率为 $\frac{1}{2}$ B、“对角线相等且相互垂直平分的四边形是正方形”这一事件是必然事件 C、“同位角相等”这一事件是不可能事件 D、“钝角三角形三条高所在直线的交点在三角形外部”这一事件是随机事件

查看试题解析
4. 如图， $l_{1}$ 平行 $l_{2}$ 平行 $l_{3}$ ，下列比例式中正确的是（）

A、 $\frac{A D}{D F} = \frac{C E}{B C}$ B、 $\frac{A D}{B E} = \frac{B C}{A F}$ C、 $\frac{C E}{D F} = \frac{A D}{B C}$ D、 $\frac{A F}{D F} = \frac{B E}{C E}$

查看试题解析
5. 若方程x²+kx﹣2＝0的一个根是﹣2，则k的值是（　　）

A、﹣1 B、1 C、0 D、﹣2

查看试题解析
6. 对于二次函数y=（x-1）²+2的图象，下列说法正确的是（　　）

A、开口向下 B、对称轴是x=-1 C、顶点坐标是（1，2） D、与x轴有两个交点

查看试题解析
7. 如图，以点O为位似中心，把△ABC放大为原图形的2倍得到 $△ A^{'} B^{'} C^{'}$ ，以下说法错误的是（）

A、S_△ABC∶S_△A’B’C=1∶2 B、AB∶ $A^{'} B^{'}$ =1∶2 C、点A，O，A’三点在同一条直线上 D、BC∥ $B^{'} C^{'}$

查看试题解析
8. 如图，点A、B、C在⊙O上，BC $//$ OA，连接BO并延长，交⊙O于点D，连接AC，DC.若∠A＝25°，则∠D的大小为（）

A、25° B、30° C、40° D、50°

查看试题解析
9.
以如图所示的方格纸中，每个小正方形的边长为1，如果以MN所在的直线为Y轴，以小正方形的边长为单位长度建立平面直角坐标系，使A点与B点关于原点对称，则这时C点的坐标可能是（）

A、（1，3）； B、（2，-1）； C、2， 1）； D、（3，1）

查看试题解析
10. 如图是二次函数 $y = a x^{2} + b x + c$ 的图象，下列结论：
① $a c > 0$ ，② $2 a + b > 0$ ，③ $4 a c < b^{2}$ ，④ $a + b + c < 0$ ，⑤当 $x > 0$ 时， $y$ 随 $x$ 的增大而减小；

其中正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 计算 $\sin^{2} 30 ° + \cos^{2} 30 ° =$ .

查看试题解析
12. 一把剪刀如图所示， $A B = 2 B C ， B D = 2 B E$ ，当手握的地方 $E C$ 张开 $3 c m$ 时，剪刀的尖端 $A$ ， $D$ 两点的距离为 $c m$

查看试题解析
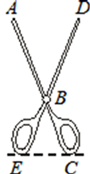13. 有一个只放满形状大小都一样的白色小球的不透明盒子，小刚想知道盒内有多少白球，于是小刚向这个盒中放了8个黑球（黑球的形状大小与白球一样），摇匀后从中随机摸出一个球记下颜色，再把它放回盒中，不断重复，共摸球400次，其中80次摸到黑球，估计盒中大约有白球．

查看试题解析
14. 如图，点A（﹣4，2）和B（2，﹣4）是一次函数y＝kx+b的图象和反比例函数y＝ $\frac{m}{x}$ 的图象的两个交点，则不等式kx+b＜ $\frac{m}{x}$ 的解集是.

查看试题解析
15. 如图，在边长为2的正方形ABCD中，以点D为圆心.AD的长为半径画弧，再以BC为直径画半圆.若阴影部分①的面积为S₁ ，阴影部分②的面积为S₂ ，则S₂-S₁的值为.

查看试题解析

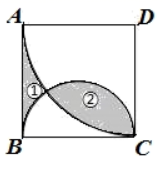
三、解答题

16. 计算： $6 \sin 45^{°} + | 2 \sqrt{2} - 7 | - {(\frac{1}{2})}^{- 3} + {(2020 - \sqrt{2020})}^{0}$

查看试题解析
17. 如图，AB是⊙O的直径，BC为⊙O的切线，D为⊙O上的一点，CD＝CB，延长CD交BA的延长线于点E.

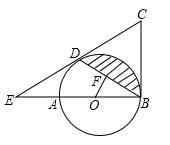(1)、求证：CD为⊙O的切线；

(2)、若OF⊥BD于点F，且OF＝2，BD＝4 $\sqrt{3}$ ，直接写出图中阴影部分的面积.

查看试题解析
18. 如图，AD是△ABC的高， $\cos B = \frac{\sqrt{2}}{2} ， \sin C = \frac{3}{5} ， A C = 10$ ，求△ABC的周长.

查看试题解析
19. 如图，一次函数y₁＝x+b的图象与与反比例函数y₂＝ $\frac{k}{x}$ （k≠0，x＜0）的图象交于点A（﹣2，1），B两点.

(1)、求一次函数与反比例函数的表达式；

(2)、求△AOB的面积.

查看试题解析
20. 如图，在 $Δ A B C$ 中，点D在 $A B$ 边上， $∠ A B C = ∠ A C D$ .

(1)、求证： $Δ A B C ∽ Δ A C D$ ；

(2)、若 $A D = 4 ， A B = 9$ 求 $A C$ 的长.

查看试题解析
21. 将分别标有数字1、2、3的3个质地和大小完全相同的小球装在一个不透明的口袋中.

(1)、若从口袋中随机摸出一个球，其标号为奇数的概率为多少？

(2)、若从口袋中随机摸出一个球，放回口袋中搅匀后再随机摸出一个球，试求所摸出的两个球上数字之和等于4的概率（用树状图或列表法求解）.

查看试题解析
22. 某超市销售一款洗手液，这款洗手液成本价为每瓶16元，当销售单价定为每瓶20元时，每天可售出60瓶．市场调查反应：销售单价每上涨1元，则每天少售出5瓶．若设这款洗手液的销售单价上涨x元，每天的销售量利润为y元．

(1)、每天的销售量为瓶，每瓶洗手液的利润是元；（用含x的代数式表示）

(2)、若这款洗手液的日销售利润y达到300元，则销售单价应上涨多少元？

(3)、当销售单价上涨多少元时，这款洗手液每天的销售利润y最大，最大利润为多少元？

查看试题解析
23. 如图，抛物线 $y = - x^{2} + b x + c$ 与x轴交于A（-1，0），B（5，0）两点，直线 $y = - x + 4$ 与y轴交于点C，与x轴交于点D.点P是x轴上方的抛物线上一动点，过点P作PF⊥x轴于点F，交直线CD于点E.设点P的横坐标为m.

(1)、求抛物线的解析式；

(2)、是否存在点P，使得△PCE与△DEF相似.若存在，求出点P的坐标，若不存在，请说明理由.

查看试题解析