河南省南阳市淅川县2021年数学中考一模试卷
试卷更新日期:2021-06-04 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 中国抗疫取得了巨大成就,堪称奇迹,为世界各国防控疫情提供了重要借鉴和支持,让中国人民倍感自豪.2020年1月12日,世界卫生组织正式将2019新型冠状病毒命名为2019-nCoV.该病毒的直径在0.000 000 08米~0.000 000 12米,将0.000 000 12用科学记数法表示为( )A、12×10-7m B、1.2×10-7m C、1.2×10-8m D、0.12×10-6m3. 下列运算正确的是( )A、a2a3=a6 B、2a+3a=5a2 C、(a+b)2=a2+b2 D、(﹣ab2)3=﹣a3b64. 如图,一条公路修到湖边时,需拐弯绕道而过,如果第一次拐的 ,第二次拐的 ,第三次拐的 ,这时的道路恰好和第一次拐弯之前的道路平行,则 是( )
 A、 B、 C、 D、5. 下列几何体是由4个相同的小正方体搭成的,其中左视图与俯视图相同的是( )A、
A、 B、 C、 D、5. 下列几何体是由4个相同的小正方体搭成的,其中左视图与俯视图相同的是( )A、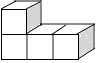 B、
B、 C、
C、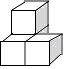 D、
D、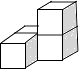 6. 下列一元二次方程中,没有实数根的是( )A、x2=2x B、x2-2x=-1 C、2x2-1=x D、2x2-2x+1=07. 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.“其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每件椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为 株,则符合题意的方程是( )A、 B、 C、 D、8. 如图,在平面直角坐标系中,Rt△ABC的顶点,B分别在y轴、x轴上,OA=2,OB=1,斜边AC∥x轴.若反比例函数(k>0,x>0)的图象经过AC的中点D,则k的值为( )
6. 下列一元二次方程中,没有实数根的是( )A、x2=2x B、x2-2x=-1 C、2x2-1=x D、2x2-2x+1=07. 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.“其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每件椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为 株,则符合题意的方程是( )A、 B、 C、 D、8. 如图,在平面直角坐标系中,Rt△ABC的顶点,B分别在y轴、x轴上,OA=2,OB=1,斜边AC∥x轴.若反比例函数(k>0,x>0)的图象经过AC的中点D,则k的值为( ) A、8 B、5 C、6 D、49. 在平面直角坐标系中,矩形ABCD的边BC在 轴上,顶点 ,连接AC按照下列方法作图:(1)以点C为圆心,适当的长度为半径画弧分别交CA,CD于点E,F;(2)分别以点E,F为圆心,大于 的长为半径画弧交于点G;(3)作射线CG交AD于H,则点H的横坐标为( )
A、8 B、5 C、6 D、49. 在平面直角坐标系中,矩形ABCD的边BC在 轴上,顶点 ,连接AC按照下列方法作图:(1)以点C为圆心,适当的长度为半径画弧分别交CA,CD于点E,F;(2)分别以点E,F为圆心,大于 的长为半径画弧交于点G;(3)作射线CG交AD于H,则点H的横坐标为( ) A、6 B、4 C、3 D、110. 如图,矩形OABC的顶点O( 0,0),B(-2,2 ),若矩形绕点O逆时针旋转,每秒旋转60°,则第145秒时,矩形的对角线交点D的坐标为( )
A、6 B、4 C、3 D、110. 如图,矩形OABC的顶点O( 0,0),B(-2,2 ),若矩形绕点O逆时针旋转,每秒旋转60°,则第145秒时,矩形的对角线交点D的坐标为( ) A、(-1, ) B、(-1,-3) C、(-2,0 ) D、(1,-3)
A、(-1, ) B、(-1,-3) C、(-2,0 ) D、(1,-3)二、填空题
-
11. 计算: =.12. 不等式组 的最大整数解为.13. 现有两个不透明的袋子,一个装有2个红球、1个白球,另一个装有1个黄球、2个红球,这些球除颜色外完全相同.从两个袋子中各随机摸出1个球,摸出的两个球颜色相同的概率是.14. 如图,在扇形AOB中,∠AOB=90°,OA=4,以OB为直径作半圆,圆心为点C,过点C作OA的平行线分别交两弧点D、E,则阴影部分的面积为.
 15. 如图,已知△ABC为等腰直角三角形,AC=BC=6,∠BCD=15°,P为直线CD上的动点,则|PA-PB|的最大值为.
15. 如图,已知△ABC为等腰直角三角形,AC=BC=6,∠BCD=15°,P为直线CD上的动点,则|PA-PB|的最大值为.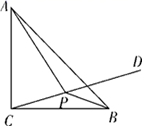
三、解答题
-
16. 先化简,再求值: ,其中 .17. 某校八、九年级各有学生200人,为了了解学生的运动状况,从八、九年级各随机抽取40名学生进行了体能测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.(说明:成绩80分及以上为优秀,70-79分为良好,60-69分为合格,60分以下为不合格)
a.八年级学生成绩的频数分布直方图如下(数据分为五组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x<100)
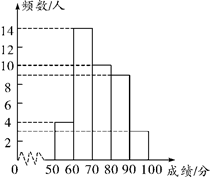
b.八年级学生成绩在70≤x<80这一组的是
70 71 73 73 73 74 76 77 78 79
c.九年级学生成绩的平均数、中位数、众数、优秀率如下:
平均数
中位数
众数
优秀率
79
76
84
40%
根据以上信息,回答下列问题:
(1)、在此次测试中,小腾的成绩是74分,在年级排名是第17名,由此可知他是年级的学生(填“八”或“九”);(2)、假设八、九年级全体学生都参加了此次测试.①预估九年级学生达到优秀的约有人;
②如果年级排名在前70名的学生可以被评选为“运动达人”,预估八年级学生至少要达到分才可以入选.
(3)、根据上述信息,推断 ▲ 年级学生运动状况更好,并说明理由.18. 如图,在△ACE中,AC=CE,⊙O经过点A,C且与边AE,CE分别交于点D,F,点 B是 上一点,且 = ,连接AB,BC,CD. (1)、求证:△CDE≌△ABC;(2)、若AC为⊙O的直径,填空:
(1)、求证:△CDE≌△ABC;(2)、若AC为⊙O的直径,填空:①当∠E=时,四边形OCFD为菱形;
②当∠E=时,四边形ABCD为正方形.
19. 河南省开封市铁塔始建于公元1049年(北宋皇佑元年),是国家重点保护文物之一,在900多年中,历经了数次地震、大风、水患而巍然屹立,素有“天下第一塔”之称.如图,小明的眼睛到地面的距离AB为1.7米,他站在点A处测得塔顶D的仰角为45°,小颖的眼睛到地面的距离EF为1.5米,她站在点E处测得塔顶D的仰角为38°.已知小明与小颖相距125米,求铁塔CD的高度.(结果精确到1米.参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78) 20. 如图,半圆 的直径 ,点 在 上且 ,点 是半圆 上的动点,过点 作 交 (或 的延长线)于点 .设 , .(当点 与点 或点 重合时, 的值为0)
20. 如图,半圆 的直径 ,点 在 上且 ,点 是半圆 上的动点,过点 作 交 (或 的延长线)于点 .设 , .(当点 与点 或点 重合时, 的值为0)
小石根据学习函数的经验,对函数 随自变量 的变化而变化的规律进行了探究.
下面是小石的探究过程,请补充完整:
(1)、通过取点、画图、测量,得到了 与 的几组值,如下表:1
1.5
2
2.5
3
3.5
4
0
3.7
a
3.8
3.3
2.5
b
上表中 a= , b=.
(2)、建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象; (3)、结合画出的函数图象,解决问题:
(3)、结合画出的函数图象,解决问题:当 与直径 所夹的锐角为 时, 的长度约为 .(结果保留一位小数)
21. 某文具店准备购进A、B两种品牌的文具袋进行销售,若购进A品牌文具袋和B品牌文具袋各5个共花费120元,购进A品牌文具袋3个和B品牌文具袋4个共花费88元.(1)、求购进A品牌文具袋和B品牌文具袋的单价;(2)、若该文具店购进了A,B两种品牌的文具袋共100个,其中A品牌文具袋售价为12元,B品牌文具袋售价为23元,设购进A品牌文具袋x个,获得总利润为w元.①求w关于x的函数关系式;
②要使销售文具袋的利润最大,且所获利润不低于进货价格的45%,请你帮该文具店设计一个进货方案,并求出其所获利润的最大值.
22. 在平面直角坐标系中,函数y=x2-2ax-1(a为常数)的图象与y轴交于点A.(1)、求点A的坐标.(2)、当此函数图象经过点(1,2)时,求此函数的表达式,并写出函数值y随x的增大而增大时x的取值范围.(3)、当x≤0时,若函数y=x2-2ax-1(a为常数)的图象的最低点到直线y=2a的距离为2,求a的值.23. 在△ABC中,AB=AC,∠BAC=α,点D为AB边上一动点,∠CDE=α,CD= ED,连接BE,EC. (1)、问题发现:
(1)、问题发现:如图①,若α=60°,则∠EBA= , AD与EB的数量关系是;
(2)、类比探究:如图②,当α=120°时,请写出∠EBA的度数及AD与EB的数量关系并说明理由;
(3)、拓展应用:如图③,点E为正方形ABCD的边AB上的三等分点,以DE为边在其上方作正方形DEFG,点O为正方形DEFG的中心,若OA= ,请直接写出线段 EF的长度.