海南省2021年数学中考二模试卷
试卷更新日期:2021-06-04 类型:中考模拟
一、单选题
-
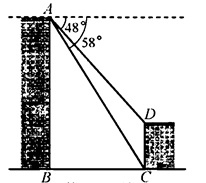
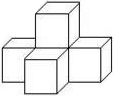
1. 有理数2021的相反数为( )A、2021 B、-2021 C、 D、2. 如图,5个完全相同的小正方体组成了一个几何体,则这个几何体的主视图是( )
 A、
A、 B、
B、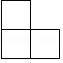 C、
C、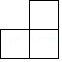 D、
D、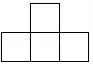 3. 下列运算正确的是( )A、 B、 C、 D、4. 2020年海南省共有57336人参加高考,将数据57336用科学记数法表示应为( )A、 B、 C、 D、5. 一元一次不等式x-1≥0的解集在数轴上表示正确的是( )A、
3. 下列运算正确的是( )A、 B、 C、 D、4. 2020年海南省共有57336人参加高考,将数据57336用科学记数法表示应为( )A、 B、 C、 D、5. 一元一次不等式x-1≥0的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 6. 如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=40°,则∠4等于( )
6. 如图,直线a,b被直线c所截,a∥b,∠1=∠2,若∠3=40°,则∠4等于( )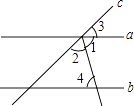 A、40° B、50° C、70° D、80°7. 如图,AB是⊙O的直径, = = ,∠COD=34°,则∠AEO的度数是( )
A、40° B、50° C、70° D、80°7. 如图,AB是⊙O的直径, = = ,∠COD=34°,则∠AEO的度数是( ) A、51° B、56° C、68° D、78°8. 已知点A(a,1)与点B(-4,b)关于原点对称,则a+b的值为( )A、5 B、-5 C、3 D、-39. 某单位定期对员工的专业知识、工作业绩、出勤情况三个方面进行考核(考核的满分均为100分),三个方面的重要性之比依次为3:5:2.小王经过考核后所得的分数依次为90、88、83分,那么小王的最后得分是( )
A、51° B、56° C、68° D、78°8. 已知点A(a,1)与点B(-4,b)关于原点对称,则a+b的值为( )A、5 B、-5 C、3 D、-39. 某单位定期对员工的专业知识、工作业绩、出勤情况三个方面进行考核(考核的满分均为100分),三个方面的重要性之比依次为3:5:2.小王经过考核后所得的分数依次为90、88、83分,那么小王的最后得分是( )
A、87 B、87.5 C、87.6 D、8810. 已知 ,则 的值是( )A、 B、 C、 D、11. 如图,扇形OAB动点P从点A出发,沿 、线段BO、OA匀速运动到点A,则OP的长度y与运动时间t之间的函数图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 12. 如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A,B分别在x轴、y轴的正半轴上,∠ABC=90°,CA⊥x轴,点C在函数y= (x>0)的图象上,若AB=2,则k的值为( )
12. 如图,在平面直角坐标系中,等腰直角三角形ABC的顶点A,B分别在x轴、y轴的正半轴上,∠ABC=90°,CA⊥x轴,点C在函数y= (x>0)的图象上,若AB=2,则k的值为( )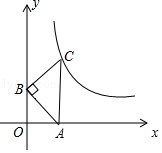 A、4 B、2 C、2 D、
A、4 B、2 C、2 D、二、填空题
-
13. 分解因式: .14. 点 P(3,﹣4)关于 y 轴对称点的坐标是 .15. 已知 ,它们的周长分别为 和 ,则 与 面积之比为.16. 一个扇形的圆心角为120°,半径为3,则这个扇形的面积为(结果保留π)
三、解答题
-
17.(1)、计算:(2)、化简: ;18. 某校需购买一批课桌椅供学生使用,已知A型课桌椅230元/套,B型课桌椅200元/套.(1)、该校购买了A,B型课桌椅250套,付款53 000元,求A,B型课桌椅各买了多少套?(2)、因学生人数增加,该校需再购买100套A,B型课桌椅,现只有资金22 000元.最多能购买A型课桌椅多少套?19. 某学校为了解八年级学生的课外阅读情况,钟老师随机抽查部分学生,并对其暑假期间的课外阅读量进行统计分析,绘制成如下不完整的统计图.根据图示信息,解答下列问题:
 (1)、被抽查学生人数为;课外阅读量的众数为;(2)、扇形统计图中的 ; ;(3)、将条形统计图补充完整;(4)、若规定:假期阅读3本以上(含3本)课外书籍者为完成假期作业,据此估计该校600名学生中,完成假期作业的有多少人?
(1)、被抽查学生人数为;课外阅读量的众数为;(2)、扇形统计图中的 ; ;(3)、将条形统计图补充完整;(4)、若规定:假期阅读3本以上(含3本)课外书籍者为完成假期作业,据此估计该校600名学生中,完成假期作业的有多少人?