贵州省贵阳市南明区2021年数学中考模拟试卷
试卷更新日期:2021-06-04 类型:中考模拟
一、单选题
-
1. 贵阳市元月份某一天早晨的气温是-3℃,中午上升了2℃,则中午的气温是( )A、-5℃ B、5℃ C、-1℃ D、1℃2. 如图,是由完全相同的5个小立方体组成的4个立体图形,主视图和左视图完全相同的( )A、
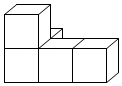 B、
B、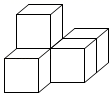 C、
C、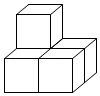 D、
D、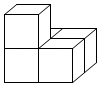 3. 光线在不同介质中的传播速度不同,因此当光线从空气射向水中时,会发生折射.如图,在空气中平行的两条入射光线,在水中的两条折射光线也是平行的.若水面和杯底互相平行,且∠1=122°,则∠2=( )
3. 光线在不同介质中的传播速度不同,因此当光线从空气射向水中时,会发生折射.如图,在空气中平行的两条入射光线,在水中的两条折射光线也是平行的.若水面和杯底互相平行,且∠1=122°,则∠2=( )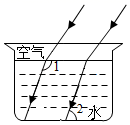 A、61° B、58° C、48° D、41°4. 下列各曲线中,不表示y是 x的函数的是( )A、
A、61° B、58° C、48° D、41°4. 下列各曲线中,不表示y是 x的函数的是( )A、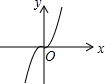 B、
B、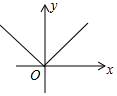 C、
C、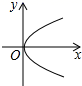 D、
D、 5. 如果有一个数不超过 ,那么这个数的取值范围在数轴上表示正确的是( )A、
5. 如果有一个数不超过 ,那么这个数的取值范围在数轴上表示正确的是( )A、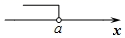 B、
B、 C、
C、 D、
D、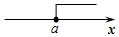 6. 快递公司快递员小张一周内投递快递物品件数情况为:有4天是每天投递65件,有2天是每天投递70件,有1天是90件,这一周小张平均每天投递物品的件数为( )A、80件 B、75件 C、70件 D、65件7. 将一枚飞镖投掷到如图所示的正六边形镖盘上,飞镖落在白色区域的概率为( )
6. 快递公司快递员小张一周内投递快递物品件数情况为:有4天是每天投递65件,有2天是每天投递70件,有1天是90件,这一周小张平均每天投递物品的件数为( )A、80件 B、75件 C、70件 D、65件7. 将一枚飞镖投掷到如图所示的正六边形镖盘上,飞镖落在白色区域的概率为( ) A、 B、 C、 D、8. 如图,一活动菱形衣架中,菱形的边长均为16cm,若墙上钉子间的距离AB=BC=16cm,则∠1等于( )
A、 B、 C、 D、8. 如图,一活动菱形衣架中,菱形的边长均为16cm,若墙上钉子间的距离AB=BC=16cm,则∠1等于( ) A、100° B、110° C、120° D、130°9. 如图,在平面直角坐标系中,△ABC关于直线m(直线m上各点的横坐标都为1)对称,点C的坐标为(4,1),则点B的坐标为( )
A、100° B、110° C、120° D、130°9. 如图,在平面直角坐标系中,△ABC关于直线m(直线m上各点的横坐标都为1)对称,点C的坐标为(4,1),则点B的坐标为( ) A、(﹣2,1) B、(﹣3,1) C、(﹣2,﹣1) D、(﹣2,﹣1)10. 如图,在平行四边形 中,点E在边 上, ,连接 交 于点F,则 的面积与 的面积之比为( )
A、(﹣2,1) B、(﹣3,1) C、(﹣2,﹣1) D、(﹣2,﹣1)10. 如图,在平行四边形 中,点E在边 上, ,连接 交 于点F,则 的面积与 的面积之比为( )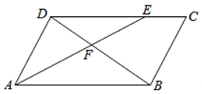 A、 B、 C、 D、11. 如图是李老师在黑板上演示的尺规作图及其步骤,
A、 B、 C、 D、11. 如图是李老师在黑板上演示的尺规作图及其步骤,已知钝角 ,尺规作图及步骤如下:
步骤一:以点 为圆心, 为半径画弧;
步骤二:以点 为圆心, 为半径画弧,两弧交于点 ;
步骤三:连接 ,交 延长线于点 .

下面是四位同学对其做出的判断:
小明说: ;
小华说: ;
小强说: ;
小方说: .
则下列说法正确的是( )
A、只有小明说得对 B、小华和小强说的都对 C、小强和小方说的都不对 D、小明和小方说的都对12. 如图,直线y= 与y轴交于点A,与直线y=﹣ 交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x﹣h)2+k的顶点在直线y=﹣ 上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( ) A、﹣2 B、﹣2≤h≤1 C、﹣1 D、﹣1
A、﹣2 B、﹣2≤h≤1 C、﹣1 D、﹣1二、填空题
-
13. 若分式 □ 运算结果为x , 则在“□”中添加的运算符号为 . (请从“+、﹣、×、÷”中选择填写)14. 袋子中有30个除颜色外完全相同的小球.在看不到球的条件下,随机地从袋子中摸出1个球,记录颜色后放回,将球摇匀.大量重复上述过程后发现,每1800次,摸到红球420次,由此可以估计口袋中的红球个数是 .15. 如图,四边形 为 的内接正四边形, 为 的内接正三角形,若 恰好是同圆的一个内接正 边形的一边,则 的值为 .
 16. 如图,菱形 中, ,点 在 边上,且 ,动点 在 边上,连接 ,将线段 绕点 顺时针旋转 至线段 ,连接 ,则线段 长的最小值为 .
16. 如图,菱形 中, ,点 在 边上,且 ,动点 在 边上,连接 ,将线段 绕点 顺时针旋转 至线段 ,连接 ,则线段 长的最小值为 .
三、解答题
-
17. 如图,菱形 的对角线交于点 ,点 是菱形外一点, , .
 (1)、求证:四边形 是矩形;(2)、连接 交 于点 ,当 , 时,求 的长度.18. 由于疫情的影响,学生不能返校上课,某校在直播授课的同时还为学生提供了四种辅助学习方式:A网上自测,B网上阅读,C网上答疑,D网上讨论.为了解学生对四种学习方式的喜欢情况,该校随机抽取部分学生进行问卷调查,规定被调查学生从四种方式中选择自己最喜欢的一种,根据调查结果绘制成如下两幅不完整的统计图:
(1)、求证:四边形 是矩形;(2)、连接 交 于点 ,当 , 时,求 的长度.18. 由于疫情的影响,学生不能返校上课,某校在直播授课的同时还为学生提供了四种辅助学习方式:A网上自测,B网上阅读,C网上答疑,D网上讨论.为了解学生对四种学习方式的喜欢情况,该校随机抽取部分学生进行问卷调查,规定被调查学生从四种方式中选择自己最喜欢的一种,根据调查结果绘制成如下两幅不完整的统计图:
根据统计图提供的信息,解答下列问题:
(1)、本次共调查了名学生;(2)、在扇形统计图中,m的值是 , D对应的扇形圆心角的度数是;(3)、请补全条形统计图;(4)、若该校共有2000名学生,根据抽样调查的结果,请你估计该校最喜欢方式D的学生人数.19. 红旺商店同时购进 、 两种商品共用人民币36000元,全部售完后共获利6000元,两种商品的进价、售价如下表:商品
商品
进价
120元/件
100元/件
售价
138元/件
120元/件
(1)、求本次红旺商店购进 、 两种商品的件数;(2)、第二次进货: 、 件数皆为第一次的2倍,销售时, 商品按原售价销售, 商品打折出售,全部售完后为使利润不少于11040元,则 商品每件的最低售价应为多少?20. 一个不透明的口袋中装有三个完全相同的小球,上面分别标有数字 ,5.(1)、从口袋中随机摸出一个小球,求摸出小球上的数字是无理数的概率(直接写出结果);(2)、先从口袋中随机摸出一个小球,将小球上的数字记为x,把小球放回口袋中并搅匀,再从口袋中随机摸出一个小球,将小球上的数字记为y.请用列表法或画树状图法求出x与y的乘积是有理数的概率.21. 如图1,某同学家的一面窗户上安装有遮阳篷,图2和图3是截面示意图,CD是遮阳篷,窗户AB为1.5米,BC为0.5米.该遮阳篷有伸缩功能.如图2,该同学在夏季某日的正午时刻测得太阳光和水平线的夹角为60°,遮阳篷CD正好将进入窗户AB的阳光挡住;如图3,该同学在冬季某日的正午时刻测得太阳光和水平线的夹角为30°,将遮阳篷收缩成CD′时,遮阳篷正好完全不挡进入窗户AB的阳光. (1)、计算图3中CD′的长度比图2中CD的长度收缩了多少米;(结果保留根号)(2)、如果图3中遮阳篷的长度为图2中CD的长度,请计算该遮阳篷落在窗户AB上的阴影长度为多少米?(请在图3中画图并标出相应字母,然后再计算)22. 如图,平行四边形 中, , ,它的边 在 轴的负半轴上,对角线 在 轴的正半轴上.反比例函数 的图象经过点 ,一次函数 的图象经过 、 两点且与反比例函数图象的另一支交于点 .
(1)、计算图3中CD′的长度比图2中CD的长度收缩了多少米;(结果保留根号)(2)、如果图3中遮阳篷的长度为图2中CD的长度,请计算该遮阳篷落在窗户AB上的阴影长度为多少米?(请在图3中画图并标出相应字母,然后再计算)22. 如图,平行四边形 中, , ,它的边 在 轴的负半轴上,对角线 在 轴的正半轴上.反比例函数 的图象经过点 ,一次函数 的图象经过 、 两点且与反比例函数图象的另一支交于点 . (1)、求反比例函数和一次函数的解析式;(2)、连接 ,求 的面积.23. 如图, 中,以 为直径的 交边 , 于 , 两点,过点 作 的切线,交 于点 ,交 的延长线于点 ,且 .
(1)、求反比例函数和一次函数的解析式;(2)、连接 ,求 的面积.23. 如图, 中,以 为直径的 交边 , 于 , 两点,过点 作 的切线,交 于点 ,交 的延长线于点 ,且 . (1)、求证: 是等腰三角形;(2)、若 , ,求线段 的长.24. 如图,抛物线 经过点 , .
(1)、求证: 是等腰三角形;(2)、若 , ,求线段 的长.24. 如图,抛物线 经过点 , . (1)、求抛物线与 轴的另一个交点 的坐标;(2)、如图①,在抛物线的对称轴上是否存在点 ,使得四边形 的周长最小?若存在,求出此时 点坐标;若不存在,请说明理由;(3)、如图②,点 是 上一动点,连接 ,在线段 上是否存在这样的点 ,使 为等腰三角形且 是直角三角形?若存在,求出点 的坐标;若不存在,请说明理由.25. 如图,我把对角线互相垂直的四边形叫做“垂美四边形”.
(1)、求抛物线与 轴的另一个交点 的坐标;(2)、如图①,在抛物线的对称轴上是否存在点 ,使得四边形 的周长最小?若存在,求出此时 点坐标;若不存在,请说明理由;(3)、如图②,点 是 上一动点,连接 ,在线段 上是否存在这样的点 ,使 为等腰三角形且 是直角三角形?若存在,求出点 的坐标;若不存在,请说明理由.25. 如图,我把对角线互相垂直的四边形叫做“垂美四边形”. (1)、性质探究:如图1.已知四边形ABCD中,AC⊥BD,垂足为O,求证:AB2+CD2=AD2+BC2 .(2)、解决问题:已知AB=5,BC=4,分别以△ABC的边BC和AB向外作等腰Rt△BCQ和等腰Rt△ABP.
(1)、性质探究:如图1.已知四边形ABCD中,AC⊥BD,垂足为O,求证:AB2+CD2=AD2+BC2 .(2)、解决问题:已知AB=5,BC=4,分别以△ABC的边BC和AB向外作等腰Rt△BCQ和等腰Rt△ABP.①如图2,当∠ACB=90°,连接PQ,求PQ;
②如图3,当∠ACB≠90°,点M、N分别是AC、AP中点连接MN.若MN= ,则S△ABC= ▲ .