广西北部湾经济区2021年数学中考一模试卷
试卷更新日期:2021-06-04 类型:中考模拟
一、单选题
-
1. 某物体如图所示,它的主视图是( )
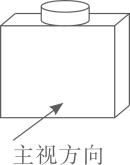 A、
A、 B、
B、 C、
C、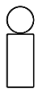 D、
D、 2. 今年春节“黄金周”期间,我市共接待游客5188900人次,将5188900用科学记数法表示为( )A、 B、 C、 D、3. 以下调查中,最适宜采用普查方式的是( )A、检测某批次汽车的抗撞击能力 B、调查黄河的水质情况 C、调查全国中学生视力和用眼卫生情况 D、检查我国“神舟八号”航天飞船各零部件的情况4. 多项式12ab3+8a3b的各项公因式是( )A、ab B、2ab C、4ab D、4ab25. 小明想做一个直角三角形的木架,以下四组木棒中,哪一组的三条能够刚好做成( )A、 、 、 B、5、12、13 C、4、5、6 D、1、 、26. 已知关于x的一元二次方程(m-1)x2+2x+1=0有实数根,则m的取值范围是( )A、m<2 B、m≤2 C、m<2且m≠1 D、m≤2且m≠17. 在平面直角坐标系中,将直线y=kx﹣6沿x轴向左平移3个单位后恰好经过原点,则k的值为( )A、﹣2 B、2 C、﹣3 D、38. 如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若AD=AC,∠A=80°,则∠ACB的度数为( )
2. 今年春节“黄金周”期间,我市共接待游客5188900人次,将5188900用科学记数法表示为( )A、 B、 C、 D、3. 以下调查中,最适宜采用普查方式的是( )A、检测某批次汽车的抗撞击能力 B、调查黄河的水质情况 C、调查全国中学生视力和用眼卫生情况 D、检查我国“神舟八号”航天飞船各零部件的情况4. 多项式12ab3+8a3b的各项公因式是( )A、ab B、2ab C、4ab D、4ab25. 小明想做一个直角三角形的木架,以下四组木棒中,哪一组的三条能够刚好做成( )A、 、 、 B、5、12、13 C、4、5、6 D、1、 、26. 已知关于x的一元二次方程(m-1)x2+2x+1=0有实数根,则m的取值范围是( )A、m<2 B、m≤2 C、m<2且m≠1 D、m≤2且m≠17. 在平面直角坐标系中,将直线y=kx﹣6沿x轴向左平移3个单位后恰好经过原点,则k的值为( )A、﹣2 B、2 C、﹣3 D、38. 如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若AD=AC,∠A=80°,则∠ACB的度数为( ) A、65° B、70° C、75° D、80°9. 如图,圆O是△ACD的外接圆,AB是圆O的直径,∠BAD=48°,则∠C的度数是( )
A、65° B、70° C、75° D、80°9. 如图,圆O是△ACD的外接圆,AB是圆O的直径,∠BAD=48°,则∠C的度数是( ) A、30° B、42° C、45° D、48°10. 如图,在正方形 中,点 是边 的中点,连接 , 交 边于点 ,已知 ,则 的长为( )
A、30° B、42° C、45° D、48°10. 如图,在正方形 中,点 是边 的中点,连接 , 交 边于点 ,已知 ,则 的长为( ) A、 B、 C、1 D、211. 甲做480个零件与乙做360个零件所用的时间相同,已知两人每天共做140个零件,若设甲每天做 个零件,则可以列出方程为( )A、 B、 C、 D、12. 如图,在第一象限的点 既在双曲线 上,又在直线 上,且直线 与 轴相交于点 , 、 ,当四边形 周长取得最小值时, ( )
A、 B、 C、1 D、211. 甲做480个零件与乙做360个零件所用的时间相同,已知两人每天共做140个零件,若设甲每天做 个零件,则可以列出方程为( )A、 B、 C、 D、12. 如图,在第一象限的点 既在双曲线 上,又在直线 上,且直线 与 轴相交于点 , 、 ,当四边形 周长取得最小值时, ( ) A、 B、 C、1 D、
A、 B、 C、1 D、二、填空题
-
13. 若分式 有意义,则字母 满足的条件是.14. 如图所示,小明为了测量学校里一池塘的宽度AB,选取可以直达A,B两点的点O处,再分别取OA,OB的中点M,N,量得MN=20m,则池塘的宽度AB为m.
 15. 如图,在Rt△ABC中,∠C=90°,AB=13,AC=5,则cosA的值是.
15. 如图,在Rt△ABC中,∠C=90°,AB=13,AC=5,则cosA的值是. 16. 在平面直角坐标系中,点 与点 关于原点对称,那么m= .17. 若 , , , ,…,则 .18. 如图,如图,在菱形 中, , ,把菱形 绕点 顺时针旋转30°得到菱形 ,其中点 的运动路径为 ,则图中阴影部分的面积为.
16. 在平面直角坐标系中,点 与点 关于原点对称,那么m= .17. 若 , , , ,…,则 .18. 如图,如图,在菱形 中, , ,把菱形 绕点 顺时针旋转30°得到菱形 ,其中点 的运动路径为 ,则图中阴影部分的面积为.
三、解答题
-
19. 计算: .20. 解方程: .21. 如图所示, 在边长为 的小正方形组成的网格中.

( 1 )将 沿 轴正方向向上平移5个单位长度后,得到 ,请作出 ,并求出 的长度;
( 2 )再将 绕坐标原点 顺时针旋转 ,得到 ,请作出 ,并直接写出点 的坐标.
22. 南宁某学校为了解七年级学生每周课外阅读时间,进行了抽样调查.并将调查结果分为3小时(记为 )、4小时(记为 )、5小时(记为 )、6小时(记为 )根据调查情况制作了两幅统计图,请你结合图中所给信息解答下列问题: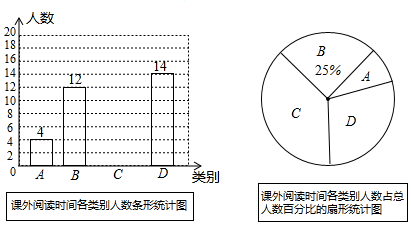 (1)、请补全条形统计图,扇形统计图中 类所对应扇形的圆心角为 ▲ 度;(2)、抽样调查阅读时间的中位数是 , 众数是.(3)、为了让学生更好的了解“新型冠状病毒”的相关知识以及防治措施,在家做好“肺炎防治”保护好自己和家人不被感染,在本次样本中,调查结果为“ ”的同学有5位来自七(1)班,分别为2位女生(记为 , )3位男生( , , ),老师准备从5位同学中选出两位共同负责在班级群中宣传肺炎的相关预防知识,请用画树状图或列表的方法求恰好选到一位男生一位女生的概率.23. 如图,△ABC中,点E在BC边上.AE=AB,将线段AC绕点A旋转到AF的位置.使得∠CAF=∠BAE.连接EF,EF与AC交于点G.
(1)、请补全条形统计图,扇形统计图中 类所对应扇形的圆心角为 ▲ 度;(2)、抽样调查阅读时间的中位数是 , 众数是.(3)、为了让学生更好的了解“新型冠状病毒”的相关知识以及防治措施,在家做好“肺炎防治”保护好自己和家人不被感染,在本次样本中,调查结果为“ ”的同学有5位来自七(1)班,分别为2位女生(记为 , )3位男生( , , ),老师准备从5位同学中选出两位共同负责在班级群中宣传肺炎的相关预防知识,请用画树状图或列表的方法求恰好选到一位男生一位女生的概率.23. 如图,△ABC中,点E在BC边上.AE=AB,将线段AC绕点A旋转到AF的位置.使得∠CAF=∠BAE.连接EF,EF与AC交于点G.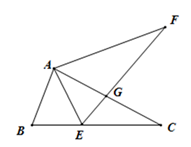 (1)、求证:EF =BC;(2)、若∠ABC=65°,∠ACB=28°,求∠FGC的度数.24. 黔东南州某超市购进甲、乙两种商品,已知购进3件甲商品和2件乙商品,需60元;购进2件甲商品和3件乙商品,需65元.(1)、甲、乙两种商品的进货单价分别是多少?(2)、设甲商品的销售单价为x(单位:元/件),在销售过程中发现:当11≤x≤19时,甲商品的日销售量y(单位:件)与销售单价x之间存在一次函数关系,x、y之间的部分数值对应关系如表:
(1)、求证:EF =BC;(2)、若∠ABC=65°,∠ACB=28°,求∠FGC的度数.24. 黔东南州某超市购进甲、乙两种商品,已知购进3件甲商品和2件乙商品,需60元;购进2件甲商品和3件乙商品,需65元.(1)、甲、乙两种商品的进货单价分别是多少?(2)、设甲商品的销售单价为x(单位:元/件),在销售过程中发现:当11≤x≤19时,甲商品的日销售量y(单位:件)与销售单价x之间存在一次函数关系,x、y之间的部分数值对应关系如表:销售单价x(元/件)
11
19
日销售量y(件)
18
2
请写出当11≤x≤19时,y与x之间的函数关系式.
(3)、在(2)的条件下,设甲商品的日销售利润为w元,当甲商品的销售单价x(元/件)定为多少时,日销售利润最大?最大利润是多少?25. 如图,在平面直角坐标系中,直线y=x+1与抛物线y=x2+bx+c交于A,B(4,5)两点,点A在x轴上.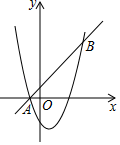 (1)、求抛物线的解析式;(2)、点E是线段AB上一动点(点A,B除外),过点E作x轴的垂线交抛物线于点F,当线段EF的长度最大时,求点E的坐标;(3)、在(2)的条件下,抛物线上是否存在一点P,使∠PEF=90°?若存在,求出点P的坐标;若不存在,说明理由.26. 在图1至图3中, 的直径 , 切 于点 , ,连接 交 于点 ,连接 , 是线段 上一点,连接 .
(1)、求抛物线的解析式;(2)、点E是线段AB上一动点(点A,B除外),过点E作x轴的垂线交抛物线于点F,当线段EF的长度最大时,求点E的坐标;(3)、在(2)的条件下,抛物线上是否存在一点P,使∠PEF=90°?若存在,求出点P的坐标;若不存在,说明理由.26. 在图1至图3中, 的直径 , 切 于点 , ,连接 交 于点 ,连接 , 是线段 上一点,连接 .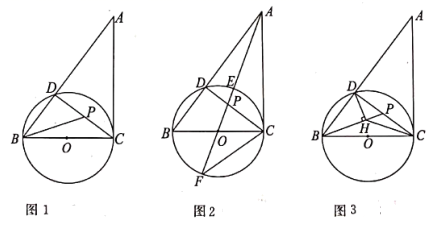 (1)、如图1,当点 , 的距离最小时,求 的长;(2)、如图2,若射线 过圆心 ,交 于点 , ,求 的值;(3)、如图3,作 于点 ,连接 ,直接写出 的最小值.
(1)、如图1,当点 , 的距离最小时,求 的长;(2)、如图2,若射线 过圆心 ,交 于点 , ,求 的值;(3)、如图3,作 于点 ,连接 ,直接写出 的最小值.