广东省深圳市三校联考2021年中考数学模拟试卷
试卷更新日期:2021-06-04 类型:中考模拟
一、选择题
-
1. ﹣ 的绝对值是( )A、﹣2020 B、﹣ C、 D、20202. 下列立体图形中,俯视图是正方形的是( )A、
 B、
B、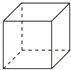 C、
C、 D、
D、 3. 流感病毒的半径大约为0.00000045米,它的直径用科学记数法表示为( )A、0.9×10﹣7 B、9×10﹣6 C、9×10﹣7 D、9×10﹣84. 2018年7月1日起,广州市全面推行生活垃圾分类.下列垃圾分类标志分别是厨余垃圾、有害垃圾、其他垃圾和可回收物,其中既是轴对称图形又是中心对称图形的是( )A、
3. 流感病毒的半径大约为0.00000045米,它的直径用科学记数法表示为( )A、0.9×10﹣7 B、9×10﹣6 C、9×10﹣7 D、9×10﹣84. 2018年7月1日起,广州市全面推行生活垃圾分类.下列垃圾分类标志分别是厨余垃圾、有害垃圾、其他垃圾和可回收物,其中既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 下列运算正确的是( )A、a+2a=3a2 B、a2•a3=a5 C、(ab)3=ab3 D、(﹣a3)2=﹣a66. 一组数据﹣2、1、1、0、2、1.这组数据的众数和中位数分别是( )A、﹣2、0 B、1、0 C、1、1 D、2、17. 如图,在△ABC中,BA=BC , ∠B=80°,观察图中尺规作图的痕迹,则∠DCE的度数为( )
5. 下列运算正确的是( )A、a+2a=3a2 B、a2•a3=a5 C、(ab)3=ab3 D、(﹣a3)2=﹣a66. 一组数据﹣2、1、1、0、2、1.这组数据的众数和中位数分别是( )A、﹣2、0 B、1、0 C、1、1 D、2、17. 如图,在△ABC中,BA=BC , ∠B=80°,观察图中尺规作图的痕迹,则∠DCE的度数为( ) A、60° B、65° C、70° D、75°8. 如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠AED'=50°,则∠EFC等于( )
A、60° B、65° C、70° D、75°8. 如图所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠AED'=50°,则∠EFC等于( )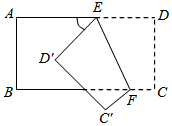 A、65° B、110° C、115° D、130°9. 如图,在A处测得点P在北偏东60°方向上,在B处测得点P在北偏东30°方向上,若AP=6 千米,则A , B两点的距离为( )千米.
A、65° B、110° C、115° D、130°9. 如图,在A处测得点P在北偏东60°方向上,在B处测得点P在北偏东30°方向上,若AP=6 千米,则A , B两点的距离为( )千米. A、4 B、4 C、2 D、610. 若关于x的一元二次方程kx2﹣x﹣ =0有实数根,则实数k的取值范围是( )A、k=0 B、k≥ C、k≥ 且k≠0 D、k>11. 已知抛物线y=ax2+bx+c与反比例函数y= 的图象在第一象限有一个公共点,其横坐标为1,则一次函数y=bx+ac的图象可能是( )A、
A、4 B、4 C、2 D、610. 若关于x的一元二次方程kx2﹣x﹣ =0有实数根,则实数k的取值范围是( )A、k=0 B、k≥ C、k≥ 且k≠0 D、k>11. 已知抛物线y=ax2+bx+c与反比例函数y= 的图象在第一象限有一个公共点,其横坐标为1,则一次函数y=bx+ac的图象可能是( )A、 B、
B、 C、
C、 D、
D、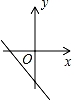 12. 如图,在Rt△ABC中,CA=CB , M是AB的中点,点D在BM上,AE⊥CD , BF⊥CD , 垂足分别为E、F , 连接EM , 则下列结论中:①BF=CE;②∠AEM=∠DEM;③CF•DM=BM•DE;④DE2+DF2=2DM2 , 其中正确结论的个数是( )
12. 如图,在Rt△ABC中,CA=CB , M是AB的中点,点D在BM上,AE⊥CD , BF⊥CD , 垂足分别为E、F , 连接EM , 则下列结论中:①BF=CE;②∠AEM=∠DEM;③CF•DM=BM•DE;④DE2+DF2=2DM2 , 其中正确结论的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
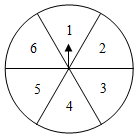
13. 分解因式:2n2﹣8= .14. 转盘中6个扇形的面积相等,任意转动转盘一次,当转盘停止转动,指针落在扇形中的数小于5的概率是 .
 15. 如图,已知反比例函数y= (x>0)与正比例函数y=x(x≥0)的图象,点A(1,4),点A′(4,b)与点B′均在反比例函数的图象上,点B在直线y=x上,四边形AA′B′B是平行四边形,则B点的坐标为 .
15. 如图,已知反比例函数y= (x>0)与正比例函数y=x(x≥0)的图象,点A(1,4),点A′(4,b)与点B′均在反比例函数的图象上,点B在直线y=x上,四边形AA′B′B是平行四边形,则B点的坐标为 .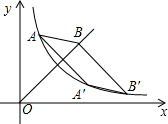 16. 对于实数p、q , 我们用符号min{p , q}表示p、q两数中较小的数,如min{1,2}=1,若min{(x﹣1)2 , x2}=1,则x= .
16. 对于实数p、q , 我们用符号min{p , q}表示p、q两数中较小的数,如min{1,2}=1,若min{(x﹣1)2 , x2}=1,则x= .三、解答题
-
17. 计算: ﹣4sin45°+( ﹣π)0﹣( )﹣1 .18. 先化简,再求值: ,其中 .19. 众志成城抗击新型冠状病毒,某校积极开展网络课程,计划开设“我们一起战疫”系列五个课程(用A , B , C , D , E表示),要求每位学生根据自己需要自主选择其中一个课程(只选一个),为此,随机调查了本校各年级部分学生选择课程的意向,并将调查结果绘制成如图的统计(不完整).

根据统计图中的信息回答下列问题:
(1)、求本校调查的学生总人数;(2)、将条形统计图补充完整;(3)、若该共有1000名学生试估计全校选择C课程的学生人数.20. 如图,在△ABC中,AB=AC,D为BC中点,AE∥BD,且AE=BD.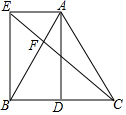 (1)、求证:四边形AEBD是矩形;(2)、连接CE交AB于点F,若∠ABE=30°,AE=2,求EF的长.21. 某工厂计划招聘A、B两个工种的工人共120人,已知A、B两个工种的工人的月工费分别为2400元和3000元.(1)、若工厂每月付A、B两个工种的总工费为330000元,那么两个工种的工人各招聘多少人.(2)、若生产需要,要求B工种的人数不少于A工种人数的2倍,那么招聘A工种的人数为多少时,可使每月支付的A、B两个工种的总工资最少.22. 如图,已知△ABC内接于⊙O , 直径AD交BC于点E , 连接OC , 过点C作CF⊥AD , 垂足为F . 过点D作⊙O的切线,交AB的延长线于点G .
(1)、求证:四边形AEBD是矩形;(2)、连接CE交AB于点F,若∠ABE=30°,AE=2,求EF的长.21. 某工厂计划招聘A、B两个工种的工人共120人,已知A、B两个工种的工人的月工费分别为2400元和3000元.(1)、若工厂每月付A、B两个工种的总工费为330000元,那么两个工种的工人各招聘多少人.(2)、若生产需要,要求B工种的人数不少于A工种人数的2倍,那么招聘A工种的人数为多少时,可使每月支付的A、B两个工种的总工资最少.22. 如图,已知△ABC内接于⊙O , 直径AD交BC于点E , 连接OC , 过点C作CF⊥AD , 垂足为F . 过点D作⊙O的切线,交AB的延长线于点G .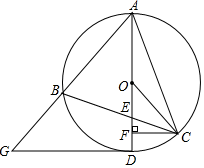 (1)、若∠G=50°,求∠ACB的度数;(2)、若AB=AE , 求证:∠BAD=∠COF;(3)、在(2)的条件下,连接OB , 设△AOB的面积为S1 , △ACF的面积为S2 , 若 ,求tan∠CAF的值.23. 抛物线y=﹣ x2﹣ x+ 与x轴交于点A , B(点A在点B的左边),与y轴交于点C , 点D是该抛物线的顶点.
(1)、若∠G=50°,求∠ACB的度数;(2)、若AB=AE , 求证:∠BAD=∠COF;(3)、在(2)的条件下,连接OB , 设△AOB的面积为S1 , △ACF的面积为S2 , 若 ,求tan∠CAF的值.23. 抛物线y=﹣ x2﹣ x+ 与x轴交于点A , B(点A在点B的左边),与y轴交于点C , 点D是该抛物线的顶点. (1)、如图1,连接CD , 则线段CD的长为;(2)、如图2,点P是直线AC上方抛物线上一点,PF⊥x轴于点F , PF与线段AC交于点E , 当PE+ EC的值最大时,求出对应的点P的坐标;(3)、如图3,点H是线段AB的中点,连接CH , 将△OBC沿直线CH翻折至△O1B1C的位置,再将△O1B1C绕点B1旋转一周,在旋转过程中,点O1 , C的对应点分别是点O2 , C1 , 直线O2C1分别与直线AC , x轴交于点M , N . 那么,在△O1B1C的整个旋转过程中,是否存在恰当的位置,使在△AMN中MN=NA成立?若存在,请直接写出所有符合条件的点C1的坐标;若不存在,请说明理由.
(1)、如图1,连接CD , 则线段CD的长为;(2)、如图2,点P是直线AC上方抛物线上一点,PF⊥x轴于点F , PF与线段AC交于点E , 当PE+ EC的值最大时,求出对应的点P的坐标;(3)、如图3,点H是线段AB的中点,连接CH , 将△OBC沿直线CH翻折至△O1B1C的位置,再将△O1B1C绕点B1旋转一周,在旋转过程中,点O1 , C的对应点分别是点O2 , C1 , 直线O2C1分别与直线AC , x轴交于点M , N . 那么,在△O1B1C的整个旋转过程中,是否存在恰当的位置,使在△AMN中MN=NA成立?若存在,请直接写出所有符合条件的点C1的坐标;若不存在,请说明理由.