福建省厦门市2021年数学中考一模试卷（5月）

试卷更新日期：2021-06-04 类型：中考模拟

进入出卷网下载

一、单选题

1. 在 $0. \overset{•}{2}$ ， $\sqrt[3]{27}$ ，﹣1， $\sqrt{3}$ 四个数中，属于无理数的是（）

A、 $0. \overset{•}{2}$ B、 $\sqrt[3]{27}$ C、﹣1 D、 $\sqrt{3}$

查看试题解析
2. 下列把2034000记成科学记数法正确的是（）

A、2.034×10⁶ B、20.34×10⁵ C、0.2034×10⁶ D、2.034×10³

查看试题解析
3. 如图所示的几何体，从上面看得到的图形是（）

A、 B、 C、 D、

查看试题解析
4. 下面计算正确的是（）

A、a³•a³＝2a³ B、2a²+a²＝3a⁴ C、a⁹÷a³＝a³ D、（﹣3a²）³＝﹣27a⁶

查看试题解析
5. 若 $m = \sqrt{10} - 1$ ，则估计m的值所在的范围是（）

A、 $0 < m < 1$ B、 $1 < m < 2$ C、 $2 < m < 3$ D、 $3 < m < 4$

查看试题解析
6. 如图，直线a∥b，则直线a，b之间距离是（）

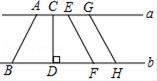A、线段AB的长度 B、线段CD的长度 C、线段EF的长度 D、线段GH的长度

查看试题解析
7. 一个正多边形的内角和为540°，则这个正多边形的每一个内角是（）

A、120° B、108° C、90° D、60°

查看试题解析
8. “红色小讲解员”演讲比赛中，7位评委分别给出某位选手的原始评分.评定该选手成绩时，从7个原始评分中去掉一个最高分、一个最低分，得到5个有效评分.5个有效评分与7个原始评分相比，这两组数据一定不变的是（）.

A、中位数 B、众数 C、平均数 D、方差

查看试题解析
9. 我国古代名著《九章算术》中有一道阐述“盈不足术”的问题，原文如下：今有人共买物，人出八，盈三；人出七，不足四，问人数几何？原文意思是：现在有一些人共同买一个物品，每人出8元，还盈余3元；每人出7元，则还差4元，问共有多少人？如果假设共有 $x$ 人，则可列方程为（）

A、 $8 x + 3 = 7 x + 4$ B、 $8 x - 3 = 7 x + 4$ C、 $8 x + 3 = 7 x - 4$ D、 $8 x - 3 = 7 x - 4$

查看试题解析
10. 二次函数 $y = 2 x^{2} + 3 x + 1$ 的图象与x轴交点的个数为（）

A、0个 B、1个 C、2个 D、1个或2个

查看试题解析

二、填空题

11. 因式分解: $x^{2} - 16 =$ .

查看试题解析
12. ${(π - 1)}^{0} =$ ； ${(- \frac{1}{3})}^{- 2} =$ ．

查看试题解析
13. 已知 $y = \sqrt{x - 3} - \sqrt{3 - x} + 2$ ，则 $x^{y} =$ ．

查看试题解析
14. 如图，在平行四边形ABCD中，E为BC边上一点，且AB=AE ，若AE平分∠DAB ， ∠EAC=25°，则∠AED的度数是度．

查看试题解析
15. 若直角三角形的两直角边长为3、4，则该直角三角形的外接圆半径为．

查看试题解析
16. 如图，矩形ABCD的两边AD ， AB的长分别为3，8，E是DC的中点，反比例函数y $= \frac{k}{x}$ （x＜0）的图象经过点E ，与AB交于点F ，连接AE ，若AF﹣AE＝2，则k的值为．

查看试题解析

三、解答题

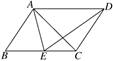
17. 解不等式组 ${\begin{array}{l} 3 x < x + 2 ， ① \\ \frac{x + 1}{2} \geq \frac{2 x + 1}{5} . ② \end{array}$ 并把解集在数轴上表示出来．

查看试题解析
18. 先化简，再求值： $(\frac{2 a}{a - 1} - \frac{a}{a + 1}) \div \frac{1}{a^{2} - 1}$ ，其中a=2

查看试题解析
19. 如图， $△ A B C$ 中，D为BC边上的一点，AD＝AC，以线段AD为边作 $△ A D E$ ，使得AE＝AB，∠BAE＝∠CAD.求证：DE＝CB.

查看试题解析
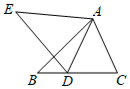20. 如图，AD与BC相交于点O，OA=OC，∠A=∠C，BE=DE.
求证：OE垂直平分BD.

查看试题解析
21. 如图

(1)、如图1，△ABC中，∠C＝90°，AB的垂直平分线交AC于点D，连接BD．若AC＝2，BC＝1，则△BCD的周长为．

(2)、O为正方形ABCD的中心，E为CD边上一点，F为AD边上一点，且△EDF的周长等于AD的长．
①图2中求作△EDF（要求：尺规作图，不写作法，保留作图痕迹）；

②图3中补全图形，直接写出∠EOF的度数．

查看试题解析
22. 在一个箱内装入只有标号不同的三颗小球，标号分别为1，2，3．每次随机取出一颗小球，记下标号作为得分，再将小球放回箱内．小明现已取球三次，得分分别为1分，3分，2分，小明又从箱内取球两次，若五次得分的平均数不小于2.2分，请用画树状图或列表的方法，求发生“五次取球得分的平均数不小于2.2分”情况的概率．

查看试题解析
23. 为迎接“国家级文明卫生城市”检查，我市环卫局准备购买 $A$ ， $B$ 两种型号的垃圾箱．通过市场调研发现：购买 $1$ 个 $A$ 型垃圾箱和2个 $B$ 型垃圾箱共需340元；购买3个 $A$ 型垃圾箱和2个 $B$ 型垃圾箱共需540元．

(1)、求每个 $A$ 型垃圾箱和 $B$ 型垃圾箱各多少元？

(2)、该市现需要购买 $A$ ， $B$ 两种型号的垃圾箱共30个，其中购买 $A$ 型垃圾箱不超过16个．
①求购买垃圾箱的总花费 $ω$ （元）与 $A$ 型垃圾箱 $x$ （个）之间的函数关系式；

②当购买 $A$ 型垃圾箱个数多少时总费用最少，最少费用是多少？

查看试题解析
24. 如图，AB是⊙O的直径， OE垂直于弦BC，垂足为F，OE交⊙O于点D，且∠CBE=2∠C.

(1)、求证：BE与⊙O相切；

(2)、若DF=9，tanC= $\frac{3}{4}$ ，求直径AB的长.

查看试题解析
25. 如图，抛物线 y＝﹣x²﹣2x+3 的图象与 x 轴交于 A、B 两点（点 A 在点 B 的左边），与 y轴交于点 C，点 D 为抛物线的顶点.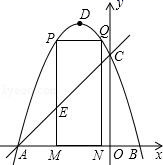

(1)、求点 A、B、C 的坐标；

(2)、点 M（m，0）为线段 AB 上一点（点 M 不与点 A、B 重合），过点 M 作 x 轴的垂线，与直线 AC 交于点 E，与抛物线交于点 P，过点 P 作 PQ∥AB 交抛物线于点 Q，过点 Q 作 QN⊥x 轴于点 N，可得矩形 PQNM.如图，点 P 在点 Q 左边，试用含 m 的式子表示矩形 PQNM 的周长；

(3)、当矩形 PQNM 的周长最大时，m 的值是多少？并求出此时的△AEM 的面积；

(4)、在（3）的条件下，当矩形 PMNQ 的周长最大时，连接 DQ，过抛物线上一点 F 作 y 轴的平行线，与直线 AC 交于点 G（点 G 在点 F 的上方）.若 FG＝2 $\sqrt{2}$ DQ，求点 F 的坐标.

查看试题解析