福建省宁德市初中毕业班2021年数学中考一模试卷
试卷更新日期:2021-06-04 类型:中考模拟
一、单选题
-
1. 计算: ( )A、-2 B、0 C、1 D、22. 下列长度的三条线段,能组成三角形的是( )A、2,3,4 B、2,3,5 C、2,2,4 D、2,2,53. 2021年2月25日习近平总书记在全国脱贫攻坚总结表彰大会上庄严宣告:“我国脱贫攻坚战取得了全面胜利,现行标准下9 899万农村贫困人口全部脱贫.” 用科学记数法表示9899万,其结果是( )A、 B、 C、 D、4. 如图,由7个大小相同的小正方体拼成的几何体,其主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 下列运算正确的是( )A、 B、 C、 D、6. 已知实数 ,则a在数轴上对应的点可能是( )
5. 下列运算正确的是( )A、 B、 C、 D、6. 已知实数 ,则a在数轴上对应的点可能是( ) A、A B、B C、C D、D7. 一组数据的方差可以用式子 表示,则式子中的数字50所表示的意义是( )A、这组数据的个数 B、这组数据的平均数 C、这组数据的众数 D、这组数据的中位数8. 如图,在反映特殊四边形之间关系的知识结构图中,①②③④表示需要添加的条件,则下列描述错误的是( )
A、A B、B C、C D、D7. 一组数据的方差可以用式子 表示,则式子中的数字50所表示的意义是( )A、这组数据的个数 B、这组数据的平均数 C、这组数据的众数 D、这组数据的中位数8. 如图,在反映特殊四边形之间关系的知识结构图中,①②③④表示需要添加的条件,则下列描述错误的是( ) A、①表示有一个角是直角 B、②表示有一组邻边相等 C、③表示四个角都相等 D、④表示对角线相等9. 如图,在⊙O中,点C是 的中点,若 ,则 的度数是( )
A、①表示有一个角是直角 B、②表示有一组邻边相等 C、③表示四个角都相等 D、④表示对角线相等9. 如图,在⊙O中,点C是 的中点,若 ,则 的度数是( ) A、 B、 C、 D、10. 七巧板是中国传统数学文化的重要载体,利用七巧板可以拼出许多有趣的图案.现用图1所示的一副七巧板拼成如图2所示的六边形,若图1中七巧板的总面积为16,则图2中六边形的周长为( )
A、 B、 C、 D、10. 七巧板是中国传统数学文化的重要载体,利用七巧板可以拼出许多有趣的图案.现用图1所示的一副七巧板拼成如图2所示的六边形,若图1中七巧板的总面积为16,则图2中六边形的周长为( )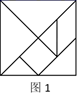
 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 实数 的相反数是.12. 因式分解: =.13. 已知七(2)班有45人,其中男生22人.现学校要从每个班中随机抽取一人组成文明督导队,则七(2)班女生被选中的概率是.14. 我国古代数学著作《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足.问鸡兔各几何.”其大意是:“有若干只鸡和兔关在同一笼子里,它们一共有35个头,94条腿.问笼中的鸡和兔各有多少只?”若列一元一次方程 表示题中的数量关系,则方程中 表示的实际意义是.15. 已知△ABC, ,AB=AC=2,分别以B,C为圆心,AB长为半径画弧,交BC于点D,E,再以DE为直径作半圆,得到如图所示的阴影图形,则该阴影图形的周长是.(结果保留 )
 16. 已知矩形ABCD,顶点A,B分别在x轴的正半轴上和y轴的正半轴上,顶点C,D在反比例函数 (k>0,x>0)的图象上.点C的横坐标是2,且矩形ABCD的面积是24,则k=.
16. 已知矩形ABCD,顶点A,B分别在x轴的正半轴上和y轴的正半轴上,顶点C,D在反比例函数 (k>0,x>0)的图象上.点C的横坐标是2,且矩形ABCD的面积是24,则k=.三、解答题
-
17. 解方程组: .18. 如图,已知AB=AD,∠C=∠E,∠BAD=∠CAE.
求证:BC=DE.
 19. 先化简,再求值:(1﹣ )÷ ,其中a= ﹣1.20. 红星运输公司要将800吨“新疆棉花”从仓储中心运往某纺织厂.现有A、B两种型号的车辆可供调用,已知A型车每辆可装30吨,B型车每辆可装25吨.现公司已确定调用12辆A型车,在每辆车不超载的前提下,要把800吨棉花一次性运完,至少需要调用B型车多少辆?21. 如图,已知矩形ABCD.
19. 先化简,再求值:(1﹣ )÷ ,其中a= ﹣1.20. 红星运输公司要将800吨“新疆棉花”从仓储中心运往某纺织厂.现有A、B两种型号的车辆可供调用,已知A型车每辆可装30吨,B型车每辆可装25吨.现公司已确定调用12辆A型车,在每辆车不超载的前提下,要把800吨棉花一次性运完,至少需要调用B型车多少辆?21. 如图,已知矩形ABCD. (1)、尺规作图:在BC上方求作△FBC,使得FB=FC,且点F与点A关于过点B的直线对称;(保留作图痕迹,不写作法)(2)、在(1)的条件下,若AB=3,BC=5,求 的值.22. 如图,已知△ABC,AB=AC,以AB为直径作⊙O交BC于点D,过点D作DE⊥AC于点E,连接OE.
(1)、尺规作图:在BC上方求作△FBC,使得FB=FC,且点F与点A关于过点B的直线对称;(保留作图痕迹,不写作法)(2)、在(1)的条件下,若AB=3,BC=5,求 的值.22. 如图,已知△ABC,AB=AC,以AB为直径作⊙O交BC于点D,过点D作DE⊥AC于点E,连接OE. (1)、求证:直线DE是⊙O的切线;(2)、若BC= ,tanC= ,求OE的长.23. 某一个小微型零件加工厂为了调动员工的生产积极性,计划采用等级基本工资加计件工资的薪酬制度,基本方案是:按工人最近三个月的平均日产量将他们分成普工、熟练工、技术能手三个等级,分别给予每月2200元,2800元和3500元的基本工资,另外再按每个零件3元给付计件工资.为确定工人等级,工厂统计了全厂30名工人最近三个月每人每天平均加工零件的个数(每个月工作时间为22天),数据如下:
(1)、求证:直线DE是⊙O的切线;(2)、若BC= ,tanC= ,求OE的长.23. 某一个小微型零件加工厂为了调动员工的生产积极性,计划采用等级基本工资加计件工资的薪酬制度,基本方案是:按工人最近三个月的平均日产量将他们分成普工、熟练工、技术能手三个等级,分别给予每月2200元,2800元和3500元的基本工资,另外再按每个零件3元给付计件工资.为确定工人等级,工厂统计了全厂30名工人最近三个月每人每天平均加工零件的个数(每个月工作时间为22天),数据如下:零件个数
15
16
17
18
19
20
21
22
25
27
29
30
31
33
人数
1
3
2
2
1
3
3
3
2
2
1
3
3
1
(1)、求这30名工人最近三个月每人每天平均加工零件个数的中位数和平均数;(2)、工厂计划将普工与技术能手的人数分别控制在25% ~ 30%之间(含25%和30%),且每月工人的工资总额不超过13万元.①若以最近三个月平均每天加工零件的个数为依据,将平均每天生产18个以下(含18个)的工人确定为普工,平均每天生产28个以上(含28个)的工人确定为技术能手,其余的工人确定为熟练工.请通过计算判断该等级划分是否符合工厂上述要求;
②请直接写出一种符合工厂要求的等级划分方案.
