广东省深圳市福田区2021年中考数学二模试卷

试卷更新日期：2021-06-04 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣5的倒数是（　　）

A、5 B、 $\frac{1}{5}$ C、﹣5 D、 $- \frac{1}{5}$

查看试题解析
2. 我国传统文化中的“福禄寿喜”图（如图）由四个图案构成．这四个图案中既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 在“百度”中搜索“深圳先行示范区”，能搜索到与之相关的信息约21700000个，若将这数据21700000用科学记数法表示为（　　）

A、0.217×10⁹ B、2.17×10⁸ C、2.17×10⁷ D、217×10⁵

查看试题解析
4. 下列运算正确的是（　　）

A、（﹣a²b³）²＝a⁴b⁶ B、a³•a⁵＝a¹⁵ C、（﹣a²）³＝﹣a⁵ D、3a²﹣2a²＝1

查看试题解析
5. 若一组数据2，4， $x$ ，5，7的平均数为5，则这组数据中的 $x$ 和中位数分别为（）

A、5，7 B、5，5 C、7，5 D、7，7

查看试题解析
6. 在平面直角坐标系中，若点P（a﹣1，a）在第二象限，则a的取值范围是（　　）

A、a＜0 B、a＞1 C、0＜a＜1 D、﹣1＜a＜0

查看试题解析
7. 如图，依据尺规作图的痕迹，计算∠α＝（）

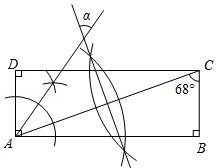A、56° B、68° C、28° D、34°

查看试题解析
8. 如图所示，点A、B、C对应的刻度分别为0、2、4、将线段CA绕点C按顺时针方向旋转，当点A首次落在矩形BCDE的边BE上时，记为点 $A_{1}$ ，则此时线段CA扫过的图形的面积为（）

A、 $4 π$ B、6 C、 $4 \sqrt{3}$ D、 $\frac{8}{3} π$

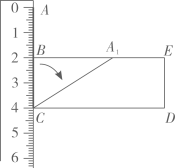查看试题解析
9. 对于实数a ， b ，定义一种新运算“⊗”为：a⊗b＝ $\frac{2}{a - b^{2}}$ ，这里等式右边是通常的实数运算．例如：1⊗3＝ $\frac{2}{1 - 3^{2}}$ ＝﹣ $\frac{1}{4}$ ，则方程x⊗（﹣1）＝ $\frac{6}{x - 1}$ ﹣1的解是（　　）

A、x＝4 B、x＝5 C、x＝6 D、x＝7

查看试题解析
10. 如图，在矩形ABCD中，AD＝ $\sqrt{2}$ AB ， ∠BAD的平分线交BC于点E ． DH⊥AE于点H ，连接BH并延长交CD于点F ，连接DE交BF于点O ，下列结论：①AD＝AE；②∠AED＝∠CED；③OE＝OD；④BH＝HF；⑤BC﹣CF＝2HE ，其中正确的有（　　）

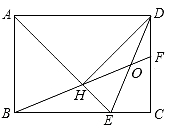A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 分解因式：2a²﹣18＝．

查看试题解析
12. 在一个不透明的盒子中装有2个白球，n个黄球，它们除颜色不同外，其余均相同．若从中随机摸出一个球，它是黄球的概率为 $\frac{3}{4}$ ，则n＝．

查看试题解析
13. 如图，无人机于空中A处测得某建筑项部B处的仰角为45°，测得该建筑底部C处的俯角为35°．若无人机的飞行高度AD为42m ，则该建筑的高度BC为m ．（参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70）．

查看试题解析
14. 如图，在△ABC中，∠BAC＝90°，AB：AC＝3：4，点D是BC上一点，AB＝BD ，连接AD ，作BE⊥AD于点E ，连接CE ，若AD＝12，则△ACE的面积为．

查看试题解析
15. 如图，菱形OABC的一边OC在x轴的正半轴上，O是原点，对角线AC和OB相交于点D ，若点C（13，0），AC•OB＝312，反比例函数y＝ $\frac{k}{x}$ （x＞0）的图象经过点D ，并与BA的延长线交于点E ，则AE＝．

查看试题解析

三、解答题

16. 计算：（﹣ $\frac{1}{4}$ ）^﹣1+2cos45°﹣|1﹣ $\sqrt{2}$ |+（3.14﹣π）⁰ ．

查看试题解析
17. 先化简，再求值：（1﹣ $\frac{1}{x + 3}$ ）÷ $\frac{x + 2}{x^{2} - 9}$ ，其中x＝3+ $\sqrt{2}$ ．

查看试题解析
18. 电子政务、数字经济、智慧社会…一场数字革命正在神州大地激荡．在第二届数字中国建设峰会召开之际，大湾区学校举行了“掌握新技术，走进数时代”信息技术应用大赛，赛后对全体参赛学生成绩按A ， B ， C ， D四个等级进行整理，得到如图所示的不完整的统计图表．

组别

频数

频率

A

5

0.1

B

a

0.4

C

15

b

D

10

0.2

(1)、参加此次比赛的学生共有人，a＝， b＝；

(2)、请计算扇形统计图中C等级对应的扇形的圆心角的度数；

(3)、已知A等级五名同学中包括来自同一班级的甲、乙两名同学，学校将从这五名同学中随机选出两名参加市级比赛，请用列表法或树状图，求甲、乙两名同学都被选中的概率．

查看试题解析
19. 某新型高科技商品，每件的售价比进价多6元，5件的进价相当于4件的售价，每天可售出200件，经市场调查发现，如果每件商品涨价1元，每天就会少卖5件．

(1)、该商品的售价和进价分别是多少元？

(2)、设每天的销售利润为w元，每件商品涨价a元，则当售价为多少元时，该商品每天的销售利润最大，最大利润为多少元？

查看试题解析
20. 如图，AB为⊙O直径，C为⊙O上的一点，过点C的切线与AB的延长线相交于点D ， CA＝CD ．

(1)、连接BC ，求证：BC＝OB；

(2)、E是 $\overset{⌢}{A B}$ 中点，连接CE ， BE ，若BE＝4，求CE的长．

查看试题解析
21. 如图1，已知抛物线y＝ax²+bx+3图象与x轴相交于A（﹣3，0），B（1，0）两点，与y轴相交于点C ．

(1)、请直接写出抛物线的解析式为．

(2)、如图1，连接AC ，若点P在y轴上时，AP和AC的夹角为15°，求线段CP的长度；

(3)、如图2，直线l与x轴相交于点M ，直线l与线段BC相交于点N ，当△MCN∽△CAM时，求直线l的表达式．

查看试题解析
22. 如图1，在平面直角坐标系中，四边形OABC的边OC在x轴上，OA在y轴上．O为坐标原点，AB∥OC ，线段OA ， AB的长分别是方程x²﹣9x+20＝0的两个根（OA＜AB）．

(1)、请求出点B的坐标；

(2)、如图2，P为OA上一点，Q为OC上一点，OQ＝5，将△POQ翻折，使点O落在AB上的点O'处，记∠AO'P＝α，∠PQO'＝β，求tanα+tanβ的值；

(3)、在（2）的条件下，M为坐标轴上一点，在平面内是否存在点N ，使以O'，Q ， M ， N为顶点四边形为矩形？若存在，请直接写出点N的坐标；若不存在，请说明理由．

查看试题解析

组别	频数	频率
A	5	0.1
B	a	0.4
C	15	b
D	10	0.2