广东省深圳市福田区2021年中考数学二模试卷

试卷更新日期：2021-06-04 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣2021的倒数是（　　）

A、﹣2021 B、﹣ $\frac{1}{2021}$ C、 $\frac{1}{2021}$ D、2021

查看试题解析
2. 2月25日，在全国脱贫攻坚总结表彰大会上，一番振聋发聩的庄重宣言，让我们再次见证了“中国式奇迹”.2012年至2020年间，中国成功实现9899万农村贫困人口全部脱贫，其中9899万用科学记数法表示为（　　）

A、9899×10⁴ B、0.9899×10⁸ C、9.899×10⁶ D、9.899×10⁷

查看试题解析
3. 下列计算中正确的是（　　）

A、 $\sqrt{{(- 3)}^{2}}$ ＝±3 B、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ C、 $\sqrt{18} \div \sqrt{2} = 3$ D、 $2 \sqrt{2} - \sqrt{2} = 2$

查看试题解析
4. 某家书店对上季度该店中国古代四大名著的销售量统计如表：

书名

《西游记》

《水浒传》

《三国演义》

《红楼梦》

销售量/本

180

120

125

85

依据统计数据，为了更好地满足读者需求，该书店决定本季度购进中国古代四大名著时多购进一些《西游记》，你认为最影响该书店决策的统计量是（　　）

A、平均数 B、众数 C、中位数 D、方差

查看试题解析
5. 不等式组 ${\begin{cases} x - 1 > 2 x + 2 \\ 2 + 5 x \leq 3 (6 - x) \end{cases}$ 的解集为（　　）

A、x＜﹣3 B、x≤2 C、﹣3＜x≤2 D、无解

查看试题解析
6. 如图，在△ABC中，按以下步骤作图：
①分别以点B ， C为圆心，大于 $\frac{1}{2}$ BC长为半径作弧，两弧相交于点M和N；

②作直线MN交AB于点D ，连接CD ．

若AB＝10，AC＝4，则△ACD的周长是（　　）

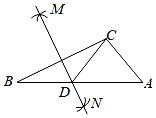A、24 B、18 C、14 D、9

查看试题解析
7. 如图，在Rt△ABC中，∠A＝90°，BC＝ $4 \sqrt{2}$ ．以BC的中点O为圆心的⊙O分别与AB ， AC相切于D ， E两点，则 $\overset{⌢}{D E}$ 的长为（　　）

A、 $\frac{π}{2}$ B、π C、2π D、4π

查看试题解析
8. 有一个模拟传染病传播的电子游戏模型：在一个方框中，先放入足够多的白球（模拟健康人），然后在框中同时放入若干个红球（模拟最初感染源）；程序设定，每经过一分钟，每个红球均恰好能使方框中R₀个白球同时变成红球（R₀为程序设定的常数）．若最初放入的白球数为400个，红球数为4个，从放入红球开始，经过2分钟后，红球总数变为了64个．则R₀应满足的方程是（　　）

A、4（1+R₀）＝64 B、4（1+R₀）＝400 C、4（1+R₀）²＝64 D、4（1+R₀）²＝400

查看试题解析
9. 二次函数y＝ax²+bx+c的图象如图所示，其对称轴是直线x＝1．下列结论：
①abc＜0；

②a+c＞b；

③4a+c＞0；

④a+b≤m（am+b）（m为实数）．

其中结论正确的个数为（　　）

A、4个 B、3个 C、2个 D、1个

查看试题解析
10. 如图，已知在Rt△ABC中，∠ACB＝90，AC＝3，BC＝ $\sqrt{3}$ ，把Rt△ABC沿着AB翻折得到Rt△ABD ，过点B作BE⊥BC ，交AD于点E ，点F是线段BE上一点，且tan∠ADF＝ $\frac{\sqrt{3}}{2}$ ．则下列结论：
①AE＝BE；

②△BED∽△ABC；

③BD²＝AD•DE；

④AF＝ $\frac{2 \sqrt{13}}{3}$ ．

其中，正确的结论是（　　）

A、①④ B、②③④ C、①②③ D、①②③④

查看试题解析

二、填空题

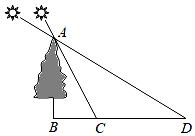
11. 因式分解：ax²﹣4a= ．

查看试题解析
12. 在一个不透明的口袋中放入只有颜色不同的白球6个，黑球4个，黄球n个，搅匀后随机摸出一个球恰好是黄球的概率是 $\frac{1}{3}$ ．则n= ．

查看试题解析
13. 如图，小明在某天15：00时测量某树的影长时，日照的光线与地面的夹角∠ACB＝60°，当他在17：00时测量该树的影长时，日照的光线与地面的夹角∠ADB＝30°，若两次测得的影长之差CD长为 $6 \sqrt{3}$ m ，则树的高度为m ．

查看试题解析
14. 如图，点M是Rt△ABC斜边AB的中点，过点M作DM⊥CM ，交AC于点D ，若AD＝2，BC＝5，则CD＝．

查看试题解析
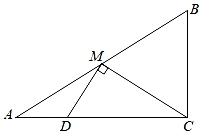15. 如图，函数y＝x与y＝ $\frac{k}{x}$ （k＞0）的图象相交于A ， B两点，P是反比例函数图象上任一点（不与A ， B重合），连接PA ， PB ．对于△ABP ，有如下性质：|∠PBA﹣∠PAB|恒为定值且等于90°．根据上述性质完成：若在图中，tan∠PAB＝ $\frac{1}{2}$ ，△PAB的面积S_△PAB＝12，则k＝．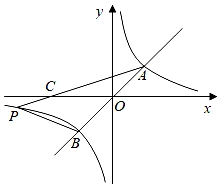

查看试题解析

三、解答题

16. 计算：2sin60°+（﹣ $\frac{1}{3}$ ）^﹣2+（π﹣2021）⁰+|2﹣ $\sqrt{3}$ |．

查看试题解析
17. 先化简，再求值：（1﹣ $\frac{3}{x + 2}$ ）÷ $\frac{x^{2} - 2 x + 1}{2 x + 4}$ ，其中x＝ $\sqrt{3}$ +1．

查看试题解析
18. 为了更好地回收、利用及处理垃圾，必需实行生活垃圾合理分类．我国目前将生活垃圾分为A：可回收垃圾；B：厨余垃圾；C：有害垃圾；D：其他垃圾，共四类．福田区某学校数学小组的同学在本区随机抽取m吨垃圾进行调查，并将调查结果制成了两幅不完整的统计图．

根据统计图提供的信息，解答下列问题：

(1)、m＝， n＝；

(2)、根据以上信息直接补全条形统计图；

(3)、扇形统计图中，厨余垃圾所对应的扇形圆心角的度数为度；

(4)、根据抽样调查的结果，请你估计在福田区随机抽取的2000吨垃圾中约有多少吨可回收垃圾？

查看试题解析
19. 如图，在平行四边形ABCD中，对角线AC ， BD交于点O ， OA＝OB ，过点B作BE⊥AC于点E ．

(1)、求证：▱ABCD是矩形；

(2)、若AD＝ $4 \sqrt{5}$ ，cos∠ABE＝ $\frac{2 \sqrt{5}}{5}$ ，求AC的长．

查看试题解析
20. 在抗击新冠肺炎疫情期间，某社区购买酒精和消毒液两种消毒物资，供居民使用．第一次分别购买酒精和消毒液若干瓶，已知酒精每瓶10元，消毒液每瓶5元，共花费了3500元；第二次又分别购买了与第一次相同数量的酒精和消毒液，由于酒精和消毒液每瓶价格分别下降了30%和20%，只花费了2600元．

(1)、求每次购买的酒精和消毒液分别是多少瓶？

(2)、若按照第二次购买的价格再一次购买，根据需要，购买的酒精数量是消毒液数量的2倍，现有购买资金2000元，则最多能购买消毒液多少瓶？

查看试题解析
21. 如图，已知在等腰△ABC中，AC＝BC ， AB＝6，高CD＝9，⊙O为△ABC的外接圆，点M是 $\overset{⌢}{A C B}$ 上一动点（不与A ， B重合），连接AM ， BM ．

(1)、如图，当射线CM与射线AB交于点E时，求证：△AMC∽△EMB；

(2)、求sin∠AMB的值；

(3)、当点M在 $\overset{⌢}{A C B}$ 上运动时，求AM•BM的最大值．

查看试题解析
22. 如图1，已知抛物线y＝ax²+bx+4与x轴交于A（﹣4，0），B（1，0）两点，与y轴交于点C ，顶点为P ．

(1)、抛物线的表达式是：；顶点P的坐标为（，）．

(2)、如图2，在抛物线的对称轴l上，有一条自由滑动的线段EF（点E在点F的上方），已知EF＝1，当|EC﹣BF|的值最大时，求四边形EFBC的面积．

(3)、如图3，沿射线AC方向或其反方向平移抛物线y＝ax²+bx+4，平移过程中A ， C两点的对应点分别记为M ， N ，抛物线顶点P的对应点记为点P'，在平移过程中，是否存在以A ， M ， B为顶点的三角形与△ABN相似，若存在，请求出此时平移后的抛物线顶点P'的坐标；若不存在，请简要说明理由．

查看试题解析

书名	《西游记》	《水浒传》	《三国演义》	《红楼梦》
销售量/本	180	120	125	85