浙江省宁波市鄞州区2021年数学中考一模试卷
试卷更新日期:2021-06-04 类型:中考模拟
一、单选题
-
1. 2021的倒数为( )A、 1202 B、-2021 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 据报道,2020年宁波GDP总量和增量双双创新高,以11985亿元的地区生产总值跃居中国内地城市第12位,其中数11985亿元用科学记数法表示为( )A、 元 B、 元 C、 元 D、 元4. 如图几何体的主视图是( )
 A、
A、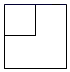 B、
B、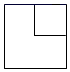 C、
C、 D、
D、 5. 疫情期间,小宁同学连续两周居家健康检测,如图是小宁记录的体温情况折线统计图,下列从图中获得的关于小宁同学的信息不正确的是( ).
5. 疫情期间,小宁同学连续两周居家健康检测,如图是小宁记录的体温情况折线统计图,下列从图中获得的关于小宁同学的信息不正确的是( ). A、第一周体温的中位数为37.1℃ B、这两周体温的众数为36.6℃ C、第一周平均体温高于第二周平均体温 D、第二周的体温比第一周的体温更加平稳6. 要使分式 有意义,则x的取值范围是( )A、 B、 C、 D、7. 已知命题:“若两个角互补,则这两个角必定一个是锐角,另一个是钝角”,下列两个角度可以说明“上述命题是假命题”的反例是( )A、40°和50° B、30°和150° C、90°和90° D、120°和150°8. 如图,将矩形纸片 的四个角向内折叠,恰好拼成一个无缝嫩、无重叠的四边形 ,若 ,则下列说法正确的是( )
A、第一周体温的中位数为37.1℃ B、这两周体温的众数为36.6℃ C、第一周平均体温高于第二周平均体温 D、第二周的体温比第一周的体温更加平稳6. 要使分式 有意义,则x的取值范围是( )A、 B、 C、 D、7. 已知命题:“若两个角互补,则这两个角必定一个是锐角,另一个是钝角”,下列两个角度可以说明“上述命题是假命题”的反例是( )A、40°和50° B、30°和150° C、90°和90° D、120°和150°8. 如图,将矩形纸片 的四个角向内折叠,恰好拼成一个无缝嫩、无重叠的四边形 ,若 ,则下列说法正确的是( ) A、 B、 C、 D、9. 如图,在平面直角坐标系中,有一系列的抛物线 (n为正整数),若 和 的顶点的连线平行于直线 ,则该条抛物线对应的n的值是( )
A、 B、 C、 D、9. 如图,在平面直角坐标系中,有一系列的抛物线 (n为正整数),若 和 的顶点的连线平行于直线 ,则该条抛物线对应的n的值是( ) A、8 B、9 C、11 D、1010. 如图,在 中, ,分别以 , , 为斜边作三个等腰直角 , , ,图中阴影部分的面积分别记为 , , , ,若已知 的面积,则下列代数式中,一定能求出确切值的代数式是( )
A、8 B、9 C、11 D、1010. 如图,在 中, ,分别以 , , 为斜边作三个等腰直角 , , ,图中阴影部分的面积分别记为 , , , ,若已知 的面积,则下列代数式中,一定能求出确切值的代数式是( )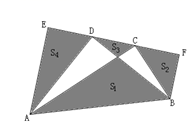 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算: 的值是.12. 分解因式: .13. 在一个不透明的袋子里装着1个白球、2个黄球、5个红球,它们除颜色不同外其余都相同.现从袋中任意摸出一个球是红球的概率为.14. 如图将母线长为9的圆锥侧面展开后得到扇形的圆心角为120°,若将该扇形剪成两个同样的扇形再围成2个同样的圆锥,则新圆锥的底面半径是.
 15. 如图,以 的对角线 上的点O为心, 为半径作圆,与 相切于点B,与 相交于点E.若 , ,则 的半径为.
15. 如图,以 的对角线 上的点O为心, 为半径作圆,与 相切于点B,与 相交于点E.若 , ,则 的半径为. 16. 如图,直线 与反比例函数 的图象交于A,B两点,与函数 在第一象限的图象交于点C, ,过点B分别作x轴,y轴的平行线交函数 在第一象限的图象于点E,D,连结 交x轴于点G,连结 交y轴于点F,连结 ,若 的面积为1,则 的值为 , 的值为.
16. 如图,直线 与反比例函数 的图象交于A,B两点,与函数 在第一象限的图象交于点C, ,过点B分别作x轴,y轴的平行线交函数 在第一象限的图象于点E,D,连结 交x轴于点G,连结 交y轴于点F,连结 ,若 的面积为1,则 的值为 , 的值为.
三、解答题
-
17.(1)、计算:(2)、解不等式组:18. 图1,图2都是由边长为1的小正三角形构成的网格,每个网格图中有3个小正三角形已涂上阴影,请在余下的小正三角形中选取1个小正三角形,涂上阴影,按下列要求分别画出符合条件的一种情形.
 (1)、在图1中画图,使得4个阴影小正三角形组成一个轴对称图形;(2)、在图2中画图,使得4个阴影小正三角形组成一个中心对称图形.19. 如图1是一种台灯,其主体部分是由与桌面垂直的固定灯杆 和可转动灯杆 和光源 组成,当灯杆 绕点B转动时,光线在桌面上的圆形照明区域随着光源到桌面的距离发生改变.图2是其示意图,其中 , ,灯杆 , .
(1)、在图1中画图,使得4个阴影小正三角形组成一个轴对称图形;(2)、在图2中画图,使得4个阴影小正三角形组成一个中心对称图形.19. 如图1是一种台灯,其主体部分是由与桌面垂直的固定灯杆 和可转动灯杆 和光源 组成,当灯杆 绕点B转动时,光线在桌面上的圆形照明区域随着光源到桌面的距离发生改变.图2是其示意图,其中 , ,灯杆 , .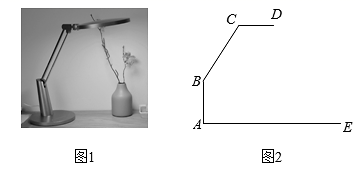 (1)、当灯杆 与 的夹角 为150°时,求光源 到桌面 的距离;(2)、若光源 到 的距离h与圆形照明区域半径r的关系是 ,要使圆形区域半径达到 ,求灯杆 与 的夹角 的度数.20. 某学校开展应急救护知识的宣传教育活动.为了解这次活动的效果,学校从全校1200名学生中随机抽取部分同学进行知识测试(测试满分100分,测试结果得分x均为不小于50的整数,且无满分).现将测试成绩分为五个等第:不合格 ,基本合格 ,合格 ,良好 ,优秀 ,制作了如下的统计图(部分信息未给出).
(1)、当灯杆 与 的夹角 为150°时,求光源 到桌面 的距离;(2)、若光源 到 的距离h与圆形照明区域半径r的关系是 ,要使圆形区域半径达到 ,求灯杆 与 的夹角 的度数.20. 某学校开展应急救护知识的宣传教育活动.为了解这次活动的效果,学校从全校1200名学生中随机抽取部分同学进行知识测试(测试满分100分,测试结果得分x均为不小于50的整数,且无满分).现将测试成绩分为五个等第:不合格 ,基本合格 ,合格 ,良好 ,优秀 ,制作了如下的统计图(部分信息未给出).
由图中给出的信息解答下列问题:
(1)、求参加测试的总人数并补全频数分布直方图:(2)、求扇形统计图中“优秀”所对应的扇形圆心角的度数:(3)、如果80分以上(包括80分)为达标,请估计全校1200名学生中成绩达标的人数.21. 如图,平面直角坐标系中,线段 的端点坐标为 , . (1)、求线段 与y轴的交点坐标;(2)、若抛物线 经过A,B两点,求抛物线的解析式;(3)、若抛物线 与线段 有两个公共点,求m的取值范围.22. 有A、B、C三个港口在同一条直线上,甲船从A港出发匀速行驶,到B港卸货1小时,以不变的速度继续匀速向前行驶最终到达C港;乙船从B港出发匀速行驶到达C港.设甲船行驶 后,甲船与B港的距离为 ,乙船与B港的距离为 ,下表记录某些时刻 与 的对应值, 与 的关系如图所示.
(1)、求线段 与y轴的交点坐标;(2)、若抛物线 经过A,B两点,求抛物线的解析式;(3)、若抛物线 与线段 有两个公共点,求m的取值范围.22. 有A、B、C三个港口在同一条直线上,甲船从A港出发匀速行驶,到B港卸货1小时,以不变的速度继续匀速向前行驶最终到达C港;乙船从B港出发匀速行驶到达C港.设甲船行驶 后,甲船与B港的距离为 ,乙船与B港的距离为 ,下表记录某些时刻 与 的对应值, 与 的关系如图所示.
0
0.5
1
2
3
4
4.5
…
60
45
30
0
0
30
45
…
(1)、甲船的行驶速度是 , 乙船的行驶速度是(2)、在图中画出 与 的图象;(3)、当甲船与乙船到港口B的距离相等时,求乙船行驶的时间.23. 定义:若一个四边形有一组邻边相等,且这组邻边夹角所对的对角线平分一个内角,则称这样的四边形为“近似菱形”. (1)、如图1,近似菱形 中, , , , 与 的夹角 所对的对角线 平分 ,求 的长;(2)、如图2,在四边形 中, , , .求证:四边形 是“近似菱形”(3)、在(2)的条件下,若 , ,求 的长.24. (提出问题)
(1)、如图1,近似菱形 中, , , , 与 的夹角 所对的对角线 平分 ,求 的长;(2)、如图2,在四边形 中, , , .求证:四边形 是“近似菱形”(3)、在(2)的条件下,若 , ,求 的长.24. (提出问题)如图1,直径 垂直弦 于点E, , ,点P是 延长线上异于点D的一个动点,连结 交 于点Q,连结 交 于点F,则点F的位置随着点P位置的改变而改变.
 (1)、(特殊位置探究)
(1)、(特殊位置探究)当 时,求 和线段 的长;
(2)、(一般规律探究)如图2,连结 , .在点P运动过程中,设 , .
①求证: ;
②求y与x之间的函数关系式:
(3)、(解决问题)当 时,求 和 的面积之比.(直接写出答案)