浙江省宁波市慈溪市2021年数学中考模拟试卷（4月）

试卷更新日期：2021-06-04 类型：中考模拟

进入出卷网下载

一、单选题

1. $\frac{1}{6}$ 的相反数是（）

A、 $\frac{1}{6}$ B、 $- 6$ C、 $6$ D、 $- \frac{1}{6}$

查看试题解析
2. 下列运算正确的是（　　）

A、 $a + 2 a = 3 a^{2}$ B、 $a^{3} \cdot a^{2} = a^{5}$ C、 ${(3 a)}^{2} = 6 a^{2}$ D、 $a^{6} \div a^{2} = a^{3}$

查看试题解析
3. 2020年，在全球经济受到新冠疫情的影响下，我国 $G D P$ 仍逆势增长2.3%，经济总量达到1016000亿元.数1016000用科学记数法表示为（　　）

A、 $1.016 \times 10^{7}$ B、 $1.016 \times 10^{6}$ C、 $1.016 \times 10^{5}$ D、 $10.16 \times 10^{5}$

查看试题解析
4. 如图是一个“凹”字形几何体，下列关于该几何体的俯视图画法正确的是（　　）

A、 B、 C、 D、

查看试题解析
5. 甲、乙、丙、丁四位同学的五次数学测验成绩统计如下表所示，如果要从这四位同学中，选出一位成绩好又稳定的同学参加数学竞赛，则应选的同学是（　　）

甲

乙

丙

丁

平均分

90

85

90

85

方差

42

50

50

42

A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 已知直线 $m / / n$ ，将一块含30°角的直角三角板 $A B C$ 按如图方式放置（ $∠ A B C = 30 °$ ），B点在直线m上，若 $∠ 1 = 25 °$ ，则 $∠ 2$ 的度数为（　　）

A、25° B、30° C、35° D、55°

查看试题解析
7. 如图，是一张矩形纸片 $A B C D$ ， $A B = 12 ， A D = 12 \sqrt{3}$ ，按如图方式剪出一张扇形纸片 $O E F$ ，O为 $B C$ 中点，弧 $E F$ 与 $A D$ 相切，把这张扇形纸片围成一个无底圆锥，则这个圆锥的底面半径为（　　）

A、 $2 \sqrt{3}$ B、2 C、 $4 \sqrt{3}$ D、4

查看试题解析
8. 《九章算术》中记录的一道题译为白话文是把一份文件用慢马送到900里外的城市，需要的时间比规定时间多一天，如果用快马送，所需的时间比规定时间少3天，已知快马的速度是慢马的2倍，求规定时间.设规定时间为 $x$ 天，则可列方程为（）

A、 $\frac{900}{x + 1} \times 2 = \frac{900}{x - 3}$ B、 $\frac{900}{x + 1} = \frac{900}{x - 3} \times 2$ C、 $\frac{900}{x - 1} \times 2 = \frac{900}{x + 3}$ D、 $\frac{900}{x + 1} = \frac{900}{x + 3} \times 2$

查看试题解析
9. 小明同学利用计算机软件绘制了某一函数的图象，如图所示.由学习函数的经验，可以推断这个函数可能是（　　）

A、 $y = \frac{- 3 x}{{(x + 2)}^{2}}$ B、 $y = \frac{- 3 x}{{(x - 1)}^{2}}$ C、 $y = \frac{3 x}{{(x + 1)}^{2}}$ D、 $y = \frac{- 3 (x + 1)}{{(x + 2)}^{2}}$

查看试题解析
10. 已知，矩形 $A B C D$ 中，E为 $A B$ 上一定点，F为 $B C$ 上一动点，以 $E F$ 为一边作平行四边形 $E F G H$ ，点 $G ， H$ 分别在 $C D$ 和 $A D$ 上，若平行四边形 $E F G H$ 的面积不会随点F的位置改变而改变，则应满足（　　）

A、 $A D = 4 A E$ B、 $A D = 2 A B$ C、 $A B = 2 A E$ D、 $A D = 3 A E$

查看试题解析

二、填空题

11. 二次根式 $\sqrt{x - 1}$ 中字母x的取值范围是．

查看试题解析
12. 分解因式：3a²﹣12= ．

查看试题解析
13. 学校组织秋游，安排九年级三辆车，小强和小明都可以从三辆
车中任选一辆搭乘，则小强和小明乘同一辆车的概率是.

查看试题解析
14. 已知命题：“关于x的一元二次方程 $x^{2} + b x + 1 = 0$ ，当 $b > 0$ 时必有实数解”，能说明这个命题是假命题的一个反例可以是.

查看试题解析
15. 如图，在 $R t Δ A B C$ 中， $∠ C = 90 ° ， ∠ B = 30 ° ， A C = 2$ ，以C为圆心，r为半径作圆.若该圆与线段 $A B$ 只有一个交点，则r的取值范围为.

查看试题解析
16. 如图，点 $A 、 C$ 分别是x轴、y轴正半轴上的点，矩形 $A B C O$ 的边 $A B ， B C$ 分别交函数 $y = \frac{k}{x}$ （ $x > 0 ， k \neq 0 ， k$ 为常数）的图象于点 $P ， Q$ ，连接 $P Q$ .

（ 1 ）若P为 $A B$ 中点，则 $\frac{B Q}{B C} =$ .

（ 2 ）若把 $Δ B P Q$ 沿 $P Q$ 翻折，点B恰好落在x轴上的点E，且 $O E = 6 ， E A = 2$ ，则 $k =$ .

查看试题解析

三、解答题

17.

(1)、计算： ${(a - 1)}^{2} + 2 (a - 2)$ ；

(2)、解不等式： $7 - x > 2 (x + 2) - 3$ .

查看试题解析
18. 图1，图2都是由边长为1的小正方形构成的网格， $Δ A B C$ 的三个顶点都在格点上，请在该 $4 \times 4$ 的网格中，分别按下列要求画一个与 $Δ A B C$ 有公共边的三角形：

(1)、使得所画出的三角形和 $Δ A B C$ 组成一个轴对称图形.

(2)、使得所画出的三角形和 $Δ A B C$ 组成一个中心对称图形.（请将两个小题依次作答在图1，图2中，均只需画出符合条件的一种情形）

查看试题解析
19. 今年的7月1日是中国共产党成立100周年纪念日，我市某中学开展了爱党宣传教育活动.为了了解这次宣传活动的效果，学校从全校1200名学生中随机抽取了部分学生进行知识测试，并将测试成绩分为 $A ， B ， C ， D ， E$ 五个等级，绘制成了如下统计图（部分信息未给出）.

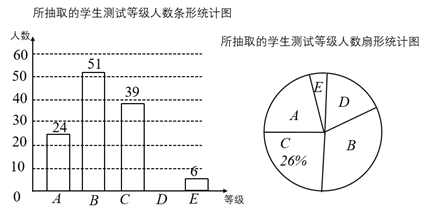(1)、求本次被调查的学生人数，并补全条形统计图.

(2)、求扇形统计图中“A”所对应的扇形圆心角的度数.

(3)、如果测试成绩为 $A 、 B$ 等级的均为优秀，请估计该校学生中成绩为优秀的人数.

查看试题解析
20. 图1是某景区的纪念币，一面有一个正十边形，示意图如图2所示，其外接圆的圆心为O，直径为 $20 mm$ .

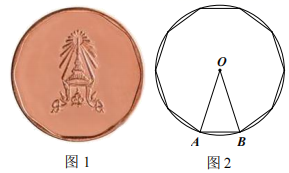(1)、求这个正十边形的边长 $A B$ .

(2)、求这个正十边形的面积.（参考数据： $\sin 18 ° \approx 0.31 ， \cos 18 ° \approx 0.95 ， \tan 18 ° \approx 0.32$ ）

查看试题解析
21. 如图，在平面直角坐标系中，二次函数 $y = a x^{2} - 2 x - 3$ 图象的顶点是A，与x轴交于 $B 、 C$ 两点，与y轴交于D，点B的坐标是 $(- 1 ， 0)$ .

(1)、求二次函数图象的顶点坐标并直接写出直线 $C D$ 的函数关系式.

(2)、作一条平行于x轴的直线交二次函数的图象于点 $M ， N$ ，与直线 $C D$ 于点R.若点 $M ， N ， R$ 的横坐标分别为 $m ， n ， r$ ，且 $r < m \leq n$ ，求 $m + n + r$ 的取值范围.

查看试题解析
22. 小聪和小慧去某风景区游览，约好在飞瀑见面.上午9：00，小聪从塔林出发，沿景区公路（如图1）步行15分钟至草甸，休息若干分钟后搭乘景区班车赶往飞瀑，车速为 $36 km/h$ .小慧也于上午9：00从古刹出发，骑自行车前往飞瀑.两人离古刹的路程y（米）与时间x（分）的函数关系如图2所示.已知古刹与塔林的路程为 $1500 m$ .

(1)、求小聪步行时离古刹的路程y（米）与时间x（分）的函数表达式.

(2)、求小聪乘坐景区班车的时间.

(3)、若小慧比小聪早到2分钟，求两人几时几分相遇.

查看试题解析
23.

(1)、（基础巩固）
如图1，在 $Δ A B C$ 中， $∠ A C B = 90 °$ ，直线 $l$ 过点C，分别过 $A 、 B$ 两点作 $A E ⊥ l ， B D ⊥ l$ ，垂足分别为 $E 、 D$ .求证： $Δ B D C \sim Δ C E A$ .

(2)、（尝试应用）
如图2，在 $Δ A B C$ 中， $∠ A C B = 90 °$ ，D是 $B C$ 上一点，过D作 $A D$ 的垂线交 $A B$ 于点E.若 $B E = D E ， \tan ∠ B A D = \frac{4}{5} ， A C = 20$ ，求 $B D$ 的长.

(3)、（拓展提高）
如图3，在 $▱ A B C D$ 中，在 $B C$ 上取点E，使得 $∠ A E D = 90 °$ ，若 $A E = A B ， \frac{B E}{E C} = \frac{4}{3} ， C D = \sqrt{14}$ ，求 $▱ A B C D$ 的面积.

查看试题解析
24. 定义：从三角形一个角的顶点引一条射线与对边相交，把这个角分成两个角，如果其中一个角与这条射线另一侧的原三角形的内角互余，那么这条射线上三角形顶点到对边交点的线段称为这个三角形的“交互线”.

(1)、判断下列命题是真命题还是假命题？
①直角三角形的斜边上的高是它的交互线；

②若三角形的角平分线是它的交互线，则这个三角形是等腰三角形.

(2)、如图1，已知 $B E$ 为锐角 $Δ A B C$ 的交互线.
①求证： $B E$ 过 $Δ A B C$ 外接圆的圆心O.

②若 $A B = A C$ ，交互线 $B E = 25$ ， $⊙ O$ 的半径为16，求 $A B$ 的长.

(3)、如图2，已知，在 $Δ A B C$ 中， $∠ C = 45 °$ ，它的两条交互线 $A D ， B E$ 相交于点F，且 $A D = m ， B E = n$ 求 $Δ A B C$ 外接圆的面积（用含 $m ， n$ 的代数式表示）.

查看试题解析

	甲	乙	丙	丁
平均分	90	85	90	85
方差	42	50	50	42