浙江省湖州市吴兴区2021年数学中考一模试卷
试卷更新日期:2021-06-04 类型:中考模拟
一、单选题
-
1. -2021的绝对值是( )A、-2021 B、2021 C、 D、2. 下列计算错误的是( )A、 B、 C、 D、3. 已知某运动队的甲、乙、丙、丁四名射击运动员平时训练的平均成绩 (单位:环)以及方差 (单位:环 )如下表,现要选一名成绩优秀且稳定的队员参加某项比赛,则应选( )
甲
乙
丙
丁
9.0
9.0
9.5
9.5
0.5
2.2
1.7
0.5
A、甲 B、乙 C、丙 D、丁4. 正六边形的每个内角的度数是( )A、 B、 C、 D、以上都不正确5. 如图,已知 中, ,则 的值为( ) A、 B、 C、 D、6. 已知:如图,点D,E分别在 , 上, ,添加一个条件,不能判定 的是( )
A、 B、 C、 D、6. 已知:如图,点D,E分别在 , 上, ,添加一个条件,不能判定 的是( ) A、 B、 C、 D、7. 不等式组 的解在数轴上表示正确的是( )A、
A、 B、 C、 D、7. 不等式组 的解在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 8. 已知点 在函数 的图象上,则下列选项中的点也在该函数图象上的是( )A、 B、 C、 D、9. 某天,甲、乙两车同时从A地出发,驶向终点B地,途中乙车由于出现故障,停车修理了一段时间,修理完毕后,乙车加快了速度匀速驶向B地;甲车从A地到B地速度始终保持不变,乙车的速度始终小于甲车的速度.甲、乙两车之间的距离 与两车出发时间 的函数图象如图所示.下列说法:①甲到达B地(终点)时,乙车距离终点还有 ;②故障排除前,乙的速度为 ;③线段 所在直线的解析式 ;④当 时,甲、乙两人之间相距60千米.其中说法正确的序号是( )
8. 已知点 在函数 的图象上,则下列选项中的点也在该函数图象上的是( )A、 B、 C、 D、9. 某天,甲、乙两车同时从A地出发,驶向终点B地,途中乙车由于出现故障,停车修理了一段时间,修理完毕后,乙车加快了速度匀速驶向B地;甲车从A地到B地速度始终保持不变,乙车的速度始终小于甲车的速度.甲、乙两车之间的距离 与两车出发时间 的函数图象如图所示.下列说法:①甲到达B地(终点)时,乙车距离终点还有 ;②故障排除前,乙的速度为 ;③线段 所在直线的解析式 ;④当 时,甲、乙两人之间相距60千米.其中说法正确的序号是( ) A、③④ B、②③ C、①②③ D、②③④10. 如图,已知在平面直角坐标系 中,点M的横坐标为3,以M为圆心,5为半径作 ,与y轴交于点A和点B,点P是 上的一动点,Q是弦 上的一个动点,延长 交 于点E,运动过程中,始终保持 ,当 的结果最大时, 长为( )
A、③④ B、②③ C、①②③ D、②③④10. 如图,已知在平面直角坐标系 中,点M的横坐标为3,以M为圆心,5为半径作 ,与y轴交于点A和点B,点P是 上的一动点,Q是弦 上的一个动点,延长 交 于点E,运动过程中,始终保持 ,当 的结果最大时, 长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 因式分解: .12. 某工厂生产了一批零件共2000件,从中任意抽取了100件进行检查,其中不合格产品2件,则可估计这批零件中约有件不合格.13. 如图,已知在菱形 中,对角线 、 相交于点O,已知AC=8,BD=4,则菱形的边长为.
 14. 中国古代的算筹计数法可追溯到公元前5世纪.摆法有纵式和横式两种(如图所示),以算筹计数的方法是摆个位为纵,十位为横,百位为纵,千位为横……这样纵横依次交替,宋代以后出现了笔算,在个位数划上斜线以表示负数,如
14. 中国古代的算筹计数法可追溯到公元前5世纪.摆法有纵式和横式两种(如图所示),以算筹计数的方法是摆个位为纵,十位为横,百位为纵,千位为横……这样纵横依次交替,宋代以后出现了笔算,在个位数划上斜线以表示负数,如 表示 ,
表示 ,  表示2369,则
表示2369,则 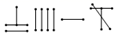 表示.
表示.  15. 图1是折叠式晾衣架,晾衣时,该晾衣架左右晾衣臂张开后的平面示意图如图2所示,支架 共有6格,将该支架六等分,撑杆 长为 ,当 水平放置时,点F卡在第三格位置,当 从水平位置绕点O逆时针旋转 时,点F绕着点D旋转了 ,卡在第一格位置的点 处,则支架 长为 (答案精确到 ,参考数据: , , , ).
15. 图1是折叠式晾衣架,晾衣时,该晾衣架左右晾衣臂张开后的平面示意图如图2所示,支架 共有6格,将该支架六等分,撑杆 长为 ,当 水平放置时,点F卡在第三格位置,当 从水平位置绕点O逆时针旋转 时,点F绕着点D旋转了 ,卡在第一格位置的点 处,则支架 长为 (答案精确到 ,参考数据: , , , ). 16. 如图,已知在平面直角坐标系 中,点A是反比例函数 的图象在第二象限分支上的一点,过点A作 轴于点B,以 为斜边在左侧作等腰 ,连结 交 于点D,过C作 的平行线交反比例函数图象于点E,且 ,则 的值是.
16. 如图,已知在平面直角坐标系 中,点A是反比例函数 的图象在第二象限分支上的一点,过点A作 轴于点B,以 为斜边在左侧作等腰 ,连结 交 于点D,过C作 的平行线交反比例函数图象于点E,且 ,则 的值是.
三、解答题
-
17. 计算:(1)、 ;(2)、 .18. 已知一辆货车上装有20吨货物,货车到达目的地后开始卸货.设平均卸货速度为v(单位:吨/小时),卸完这批货物所需的时间为t(单位:小时).(1)、求v关于t的函数表达式.(2)、若要求不超过4小时卸完车上的这批货物,那么平均每小时至少要卸货多少吨?19. 如图,在方格纸中,每个小正方形的边长都是1,点A,B,P都在格点上,请按要求画出图形,使点P在所画图形的内部(不包括边界上).
 (1)、请在图1中作出一个 ,点C和点D都在格点上;(2)、请在图2中画一个四边形 ,使得 ,且 是钝角,点E和点F都在格点上.(温馨提示:请画在答题卷相对应的图上)20. 某班组织学生进行交通安全知识竞赛活动,竞赛成绩分为A、B、C、D四个等级,根据竞赛成绩分别制作了条形统计图和扇形统计图.
(1)、请在图1中作出一个 ,点C和点D都在格点上;(2)、请在图2中画一个四边形 ,使得 ,且 是钝角,点E和点F都在格点上.(温馨提示:请画在答题卷相对应的图上)20. 某班组织学生进行交通安全知识竞赛活动,竞赛成绩分为A、B、C、D四个等级,根据竞赛成绩分别制作了条形统计图和扇形统计图.
请根据相关信息,解答下列问题:
(1)、求该班的学生总人数,并补全条形统计图;(温馨提示:请画在答题卷相对应的图上)(2)、求出扇形统计图中C等级所对应的扇形圆心角度数;(3)、已知A等的5名学生中有3名男生,2名女生,现从这5名学生中抽取两名同学参加校级竞赛,用树状图或列表法求出被抽到的两名学生恰好是一名男生,一名女生的概率.21. 如图,已知 是 的直径,点D,C是圆上的两个点,且 ,直线 于点E. (1)、求证: 是 的切线;(2)、若 ,求阴影部分的面积.22. 某特产专卖店销售某种特产,其进价为每千克120元,按每千克200元出售.为了促销,营销部门建议:顾客一次购买这种特产不超过20千克时,每千克按200元销售;若一次购买该特产超过20千克时,每多购买1千克,销售单价降低2元,但销售单价均不低于m元.该专卖店某次销售该特产所获得的的利润w(元)与购买数量x(千克)之间的函数关系如图所示.根据以上信息解决下列问题:
(1)、求证: 是 的切线;(2)、若 ,求阴影部分的面积.22. 某特产专卖店销售某种特产,其进价为每千克120元,按每千克200元出售.为了促销,营销部门建议:顾客一次购买这种特产不超过20千克时,每千克按200元销售;若一次购买该特产超过20千克时,每多购买1千克,销售单价降低2元,但销售单价均不低于m元.该专卖店某次销售该特产所获得的的利润w(元)与购买数量x(千克)之间的函数关系如图所示.根据以上信息解决下列问题: (1)、顾客购买该特产50千克时,该特产的销售单价m为每千克元,专卖店的销售利润为元;(2)、当一次购买该特产超过20千克时,求w与x之间的函数表达式;(3)、在试销期间销售人员发现:当顾客购买特产超过某一数量时,会出现随着数量的增加,专卖店所获利润反而减少这一情况.在这种情况下,为使销售量越多,专卖店所获利润越大,专卖店应将最低销售单价至少调整为每千克多少元?(其它销售条件不变)
(1)、顾客购买该特产50千克时,该特产的销售单价m为每千克元,专卖店的销售利润为元;(2)、当一次购买该特产超过20千克时,求w与x之间的函数表达式;(3)、在试销期间销售人员发现:当顾客购买特产超过某一数量时,会出现随着数量的增加,专卖店所获利润反而减少这一情况.在这种情况下,为使销售量越多,专卖店所获利润越大,专卖店应将最低销售单价至少调整为每千克多少元?(其它销售条件不变)
