新疆塔城地区乌苏市2021年数学中考一模试卷
试卷更新日期:2021-06-04 类型:中考模拟
一、单选题
-
1. 如果温度上升 ,记作 ,那么温度下降 记作( )A、 B、 C、 D、2. 下列四个几何体中,左视图为圆的是( )A、
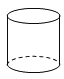 B、
B、 C、
C、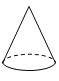 D、
D、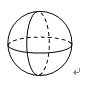 3. 若 ,则 的值是( )A、4 B、3 C、2 D、14. 下列计算正确的是( )A、 B、 C、 D、5. 关于x的一元一次不等式 的解集为 ,则m的值为( )A、14 B、7 C、 D、26. 某乡镇决定对一段长6 000米的公路进行修建改造.根据需要,该工程在实际施工时增加了施工人员,每天修健的公路比原计划增加了50%,结果提前4天完成任务.设原计划每天修建x米,那么下面所列方程中正确的是( )A、 B、 C、 D、7. 如图,在平面直角坐标系中,直线 和 相交于点 ,则不等式 的解集为( )
3. 若 ,则 的值是( )A、4 B、3 C、2 D、14. 下列计算正确的是( )A、 B、 C、 D、5. 关于x的一元一次不等式 的解集为 ,则m的值为( )A、14 B、7 C、 D、26. 某乡镇决定对一段长6 000米的公路进行修建改造.根据需要,该工程在实际施工时增加了施工人员,每天修健的公路比原计划增加了50%,结果提前4天完成任务.设原计划每天修建x米,那么下面所列方程中正确的是( )A、 B、 C、 D、7. 如图,在平面直角坐标系中,直线 和 相交于点 ,则不等式 的解集为( ) A、 B、 C、 D、8. 如图,已知圆柱的底面直径BC= ,高AB=3,小虫在圆柱表面爬行,从C点爬到A点,然后再沿另一面爬回C点,则小虫爬行的最短路程为( )
A、 B、 C、 D、8. 如图,已知圆柱的底面直径BC= ,高AB=3,小虫在圆柱表面爬行,从C点爬到A点,然后再沿另一面爬回C点,则小虫爬行的最短路程为( ) A、 B、 C、 D、9. 如图,在平面直角坐标系中,菱形 的边 在 轴的正半轴上,反比例函数 的图象经过对角线 的中点 和顶点 .若菱形 的面积为12,则 的值为( ).
A、 B、 C、 D、9. 如图,在平面直角坐标系中,菱形 的边 在 轴的正半轴上,反比例函数 的图象经过对角线 的中点 和顶点 .若菱形 的面积为12,则 的值为( ).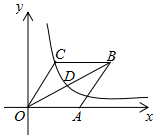 A、6 B、5 C、4 D、3
A、6 B、5 C、4 D、3二、填空题
-
10. 已知直线 ,将一块含 角的直角三角板ABC按如图所示方式放置( ),并且顶点A , C分别落在直线a , b上,若 ,则 的度数是 .
 11. 分解因式: .12. 中国人民银行近期下发通知,决定自2019年4月30日停止兑换第四套人民币中菊花1角硬币。如图所示,则该硬币边缘镌刻的正多边形的外角的度数为 。
11. 分解因式: .12. 中国人民银行近期下发通知,决定自2019年4月30日停止兑换第四套人民币中菊花1角硬币。如图所示,则该硬币边缘镌刻的正多边形的外角的度数为 。 13. 大数据分析技术为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的苏康码(绿码)示意图,用黑白打印机打印于边长为2cm的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的总面积约为 .
13. 大数据分析技术为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的苏康码(绿码)示意图,用黑白打印机打印于边长为2cm的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的总面积约为 . 14. 我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”意思是:今有一圆柱形木材,埋在墙壁中,不知其大小.用锯去锯这木材,锯口深 寸,锯道长 尺(1尺=10寸).问这根圆形木材的直径是寸.
14. 我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”意思是:今有一圆柱形木材,埋在墙壁中,不知其大小.用锯去锯这木材,锯口深 寸,锯道长 尺(1尺=10寸).问这根圆形木材的直径是寸.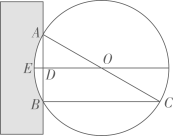 15. 抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,其与x轴的一个交点坐标为(﹣3,0),对称轴为x=﹣1,则当y<0时,x的取值范围是.
15. 抛物线y=ax2+bx+c(a≠0)的部分图象如图所示,其与x轴的一个交点坐标为(﹣3,0),对称轴为x=﹣1,则当y<0时,x的取值范围是.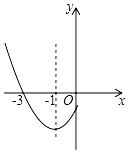
三、解答题
-
16. 计算: .17. 已知18. 如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点.点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD、AN.
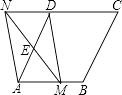 (1)、求证:四边形AMDN是平行四边形;(2)、填空:①当AM的值为时,四边形AMDN是矩形;
(1)、求证:四边形AMDN是平行四边形;(2)、填空:①当AM的值为时,四边形AMDN是矩形;②当AM的值为时,四边形AMDN是菱形.
19. 某校研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干名学生的兴趣爱好,并将调查结果绘制成下面两幅不完整的统计图,请你根据图中提供的信息解答下列问题: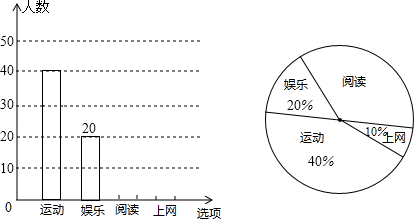 (1)、在这次调查中,一共调查了名学生;(2)、补全条形统计图;(3)、若该校共有1500名学生,估计爱好运动的学生有人;(4)、在全校同学中随机选取一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生的概率是.20. 如图,某数学兴趣小组为测量一棵古树的高度,在距离古树A点处测得古树顶端D的仰角为30°,然后向古树底端C步行20米到达点B处,测得古树顶端D的仰角为 ,且点A、B、C在同一直线上,求古树CD的高度.(结果保留根号)
(1)、在这次调查中,一共调查了名学生;(2)、补全条形统计图;(3)、若该校共有1500名学生,估计爱好运动的学生有人;(4)、在全校同学中随机选取一名学生参加演讲比赛,用频率估计概率,则选出的恰好是爱好阅读的学生的概率是.20. 如图,某数学兴趣小组为测量一棵古树的高度,在距离古树A点处测得古树顶端D的仰角为30°,然后向古树底端C步行20米到达点B处,测得古树顶端D的仰角为 ,且点A、B、C在同一直线上,求古树CD的高度.(结果保留根号)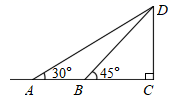 21. 某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,该山区组织村民加工包装土特产销售给游客,以增加村民收入.已知某种土特产每袋成本10元,试销阶段每袋的销售价x(元)与该土特产的日销售量y(袋)之间的关系如表:
21. 某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,该山区组织村民加工包装土特产销售给游客,以增加村民收入.已知某种土特产每袋成本10元,试销阶段每袋的销售价x(元)与该土特产的日销售量y(袋)之间的关系如表:x(元)
15
20
30
……
y(袋)
25
20
10
……
(1)、若日销售量y(袋)是每袋的销售价x(元)的一次函数,求y与x之间的函数关系式;(2)、假设后续销售情况与试销阶段效果相同,设每日销售土特产的利润为w(元);①求w与x之间的函数关系式;
②要使这种土特产每日销售的利润最大,每袋的销售价应定为多少元?每日销售的最大利润是多少元?
22. 如图,AB是 的直径,AC是 的一条弦,点P是 上一点,且PA=PC , PD//AC , 与BA的延长线交于点D.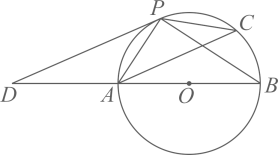 (1)、求证:PD是 的切线;(2)、若tan∠PAC= ,AC = 12.求直径AB的长.23. 如图,抛物线y=ax2+bx+2与x轴交于A,B两点,且OA=2OB,与y轴交于点C,连接BC,抛物线对称轴为直线x= ,D为第一象限内抛物线上一动点,过点D作DE⊥OA于点E,与AC交于点F,设点D的横坐标为m.
(1)、求证:PD是 的切线;(2)、若tan∠PAC= ,AC = 12.求直径AB的长.23. 如图,抛物线y=ax2+bx+2与x轴交于A,B两点,且OA=2OB,与y轴交于点C,连接BC,抛物线对称轴为直线x= ,D为第一象限内抛物线上一动点,过点D作DE⊥OA于点E,与AC交于点F,设点D的横坐标为m.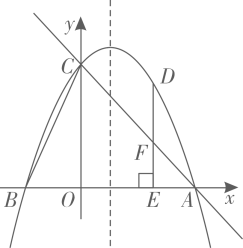 (1)、求抛物线的表达式;(2)、当线段DF的长度最大时,求D点的坐标;(3)、抛物线上是否存在点D,使得以点O,D,E为顶点的三角形与 相似?若存在,求出m的值;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、当线段DF的长度最大时,求D点的坐标;(3)、抛物线上是否存在点D,使得以点O,D,E为顶点的三角形与 相似?若存在,求出m的值;若不存在,请说明理由.