四川省成都市天府新区2021年数学中考二诊试卷

试卷更新日期：2021-06-04 类型：中考模拟

进入出卷网下载

一、单选题

1. $- 2021$ 的相反数是（）

A、 $\frac{1}{2021}$ B、 $- \frac{1}{2021}$ C、2021 D、 $- 2021$

查看试题解析
2. 用一平面去截正方体，得到截面的形状不可能是（）

A、三角形 B、四边形 C、五边形 D、七边形

查看试题解析
3. 据新闻报道：2020年11月10日8时12分，中国“奋斗者”号载人潜水器在马里亚纳海沟成功坐底，坐底深度10909米，此时“奋斗者”号承受的水压接近110兆帕（1兆帕 $= 1000000$ 帕），请你用科学记数法表示110兆帕（）

A、 $1.1 \times 10^{7}$ B、 $1.1 \times 10^{8}$ C、 $1.1 \times 10^{6}$ D、 $1.1 \times 10^{9}$

查看试题解析
4. 在平面直角坐标系中，将抛物线 $y = 2 {(x - 1)}^{2} + 3$ 先向左平移2个单位，再向下平移1个单位，得到的抛物线解析式为（）

A、 $y = 2 {(x + 1)}^{2} + 2$ B、 $y = 2 {(x - 3)}^{2} + 2$ C、 $y = 2 {(x + 1)}^{2} + 4$ D、 $y = 2 {(x - 3)}^{2} + 4$

查看试题解析
5. 下面计算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 ${(- 2 a^{2})}^{3} = - 8 a^{6}$ C、 $a^{9} \div a^{3} = a^{3}$ D、 $2 a^{2} + a^{2} = 3 a^{4}$

查看试题解析
6. 若关于x的方程 $\frac{a x}{x - 1} = \frac{2}{x - 1} + 1$ 无解，则a的值是（）

A、1 B、3 C、 $- 1$ 或2 D、1或2

查看试题解析
7. 在 $R t △ A B C$ 中， $∠ C = 90 °, B C = 5, A B = 13$ ，则 $\sin B$ 的值是（）

A、 $\frac{12}{13}$ B、 $\frac{5}{13}$ C、 $\frac{12}{5}$ D、 $\frac{5}{12}$

查看试题解析
8. 水产养殖中常采用“捉-放-捉”的方式估计一个鱼塘中鱼的数量，如从某个鱼塘中随机地捞出100条鱼，将这些鱼作上记号后再放回鱼塘，隔数日后再从该鱼塘随机捞出144条鱼，其中带有记号的有6条，从而估计该鱼塘有（）条鱼

A、1600 B、2400 C、1800 D、2000

查看试题解析
9. 如图，在四边形 $A B C D$ 中， $A D / / B C$ ； $A B = A D = D C = 1 ， B D ⊥ C D$ ，则四边形 $A B C D$ 的面积为（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{3 \sqrt{3}}{2}$ C、 $\frac{3 \sqrt{3}}{4}$ D、 $\sqrt{3}$

查看试题解析
10. 如图是二次函数 $y = a x^{2} + b x + c$ 的部分图象，图象过点 $A (3 ， 0)$ ，对称轴为 $x = 1$ ，给出下面五个结论：① $b^{2} > 4 a c$ ；② $2 a + b = 1$ ；③ $a - b + c = 0$ ；④ $b + c < 0$ ；⑤若 $y < 0$ ，则 $- 1 < x < 3$ .其中正确的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 若 $| a - 2 | = 1$ ，则a= ．

查看试题解析
12. 已知一次函数 $y = - 2 x + 1$ ，若 $- 2 \leq x \leq 1$ ，则y的最小值为.

查看试题解析
13. 小华根据朗诵比赛中9位评委所给的分数作了如下表格：

平均数

中位数

众数

方差

8.8

8.7

8.7

0.11

如果去掉一个最高分和一个最低分，则表中数据一定不发生变化的是.

查看试题解析
14. 如图， $A B ⊥ B D ， C D ⊥ B D$ ，当点P满足 $P A = P C ， ∠ A P C = 90 °$ 时，若 $A B = 2 ， \tan ∠ A P B = \frac{1}{2}$ ，则 $B D =$ .

查看试题解析
15. 若 $x - y = 2, x y = 3$ ，则代数式 $x^{3} y - 2 x^{2} y^{2} + x y^{3}$ 的值为.

查看试题解析
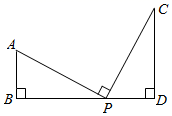16. “干支纪年法”是我国历法的一种传统纪年法，甲､乙､丙､丁､戊､已､庚､辛､壬､癸被称为“十天干”：子､丑､寅､卯､辰､已､午､未､申､酉､戍､亥叫做“十二地支”；“天干”以“甲”字开始，“地支”以“子”字开始，两者按干支顺序相配，组成了干支纪年法，其相配顺序为甲子､乙丑､丙寅…癸酉；甲戌､乙亥､丙子…癸未；甲申､乙酉､丙戌…癸已；…共得到60个组合，称六十甲子，周而复始，无穷无尽.2021年是“干支纪年法”中的辛丑年，那么2050年是“干支纪年法“中的.

查看试题解析
17. 如图，在直角 $△ A B C$ 中， $∠ A = 90 ° ， A B = 3 ， A C = 4$ ，四边形 $A D E F$ 为 $△ A B C$ 的内接正方形，若在 $△ A B C$ 内取一点，这点取自正方形 $A D E F$ 的概率为.

查看试题解析
18. 将一副三角板如图放置在一起，使得等腰直角 $△ A B D$ 与直角 $△ A C D$ 的斜边重合，其中 $A D = 4 ， ∠ B = ∠ C = 90 ° ， ∠ C A D = 30 °$ ，则点B到边 $A C$ 的距离为.

查看试题解析
19. 反比例函数 $y = \frac{1}{x}$ 的图象与一次函数 $y = 2 x + b$ 的图象相交于 $A ， B$ 两点，若 $A ， B$ 两点的横坐标分别为 $x_{1} ， x_{2}$ ，则 $| x_{1} - x_{2} |$ 的最小值为.

查看试题解析

三、解答题

20.

(1)、计算： $2 \sin 45 ° + \sqrt{{(1 - \sqrt{2})}^{2}} + {(- \frac{\sqrt{2}}{2})}^{- 1} + {(π - 3)}^{0}$ ；

(2)、解不等式组 ${\begin{array}{l} 2 x - 1 ⩾ x + 2 \\ \frac{x + 1}{2} > \frac{2 x - 1}{3} \end{array}$ .

查看试题解析
21. 先化简，再求值： $(3 - \frac{2}{x + 1}) \div \frac{3 x^{2} + x}{x + 1}$ ，其中 $x = \sqrt{3} + 1$ .

查看试题解析
22. 2021年2月25日上午，全国脱贫攻坚总结表彰大会在北京人民大会堂隆重举行，大会对全国脱贫攻坚先进个人､先进集体进行了表彰，“精准扶贫”是新时期党和国家扶贫工作的精髓和亮点，某校团委随机抽取九年级部分学生，对他们是否了解“精准扶贫”政策的情况进行调查，调查结果分为四类，分别为：A类：非常了解，B类：了解，C类：基本了解，D类：不了解.并将调查的数据绘制成如图两幅不完整的统计图，请根据统计图中的信息解决下列问题：

(1)、本次被抽样调查学生的总人数是人；

(2)、该校九年级共有800人，请估计基本了解的人数约为人；

(3)、若调查人员想从5名学生（分别记为 $a ， b ， c ， d ， e$ ）中随机选取两人，调查他们对“精准扶贫”政策的了解情况，请用列表或政树状围的方法，求同时选中 $a ， e$ 两人的概率.

查看试题解析
23. 为保护师生健康，新都某中学在学校门口安装了红外测温通道，对进校师生进行体温监测，测温装置安装在E处.某同学进校时，当他在地面D处，开始显示测量体温，此时在其额头A处测得E的仰角为 $30 °$ ，当他走到地面C处，结束显示体温，此时在其额头B处测得E的仰角为 $45 °$ ，已知该同学脚到额头的高度为 $A D$ ，且 $A D = 1.6$ 米， $C D = 1$ 米，求测温装置E距地面的高度约为多少米？（保留小数点后两位有效数字， $\sqrt{3} \approx 1.73$ ）

查看试题解析
24. 已知在平面直角坐标系中，点 $A (1 ， 2)$ 在反比例函数 $y = \frac{k}{x}$ 的图象上，过点A的直线与该双曲线的另一支交于点 $B (- 2 ， m)$ .

(1)、求直线 $A B$ 的函数表达式；

(2)、若点C为x轴上一动点，求当 $S_{△ A B C} = 6$ 时，点C的坐标.

查看试题解析
25. 如图，在正方形 $A B C D$ 中， $B C = 4 ， G$ 为射线 $C B$ 上的动点，连接 $D G$ ，交 $A C$ 于 $H$ .

(1)、证明： $△ A H B ≌ △ A H D$ ；

(2)、若 $D G$ 交 $A B$ 于 $F$ ，当 $F B = F H$ 时，求 $B G$ 之长；

(3)、是否存在点G，使得 $△ G H C$ 为等腰三角形，若存在，请求出 $C G$ 之长；若不存在，请说明理由.

查看试题解析
26. 为应对全球变暖，落实国家节能减排政策，某公司积极进行技术创新，将原本直接排放进大气中的二氧化碳转化为固态形式的化工产品，从而实现“变废为宝､低碳排放”.经过生产实践和数据分析，在这种技术下，该公司二氧化碳月处理成本y（万元）与二氧化碳月处理量 $x$ （ $2 \leq x \leq 6$ ，单位：百吨）之间满足二次函数关系，如图所示，已知点 $A (2 ， 2)$ ，顶点 $B (3 ， 1.5)$ ，假设每处理一百吨二氧化碳得到的化工产品的收入为2万元.

(1)、求该公司二氧化碳月处理成本y（万元）与二氧化碳月处理量x（ $2 \leq x \leq 6$ ，单位：百吨）之间满足的二次函数一般式；

(2)、该公司利用这种技术处理二氧化碳的最大月收益W是多少万元？（月收益=月收入-月处理成本）

查看试题解析
27. 将矩形 $A B C D$ 折叠，使得点C落在边 $A B$ 上，折痕为 $E F$ ，

(1)、如图1，当点C与点A重合时，若 $A B = 4 ， B F = 3$ ，求 $A E$ 的长；

(2)、如图2，点C落在 $A B$ 边的点M处（不与 $A ， B$ 重合），若 $A B = 4 ， A D = 8$ ，
①取 $E F$ 的中点O，连接并延长 $M O$ 与 $D^{'} E$ 的延长线交于点P，连接 $P F ， M E$ .求证：四边形 $M F P E$ 是平行四边形；

②设 $B M = t$ ，用含有t的式子表示四边形 $A B F E$ 的面积，并求四边形 $A B F E$ 的面积的最大值及此时t的值.

查看试题解析
28. 如图所示：二次函数 $y = x^{2} - x - 6$ 的图象与x轴交于 $A ， B$ 两点，与y轴交于点C，连接 $A C ， B C$ .

(1)、求直线 $B C$ 的函数表达式；

(2)、如图1，若点M为抛物线上线段 $B C$ 右侧的一动点，连接 $C M ， B M$ .求 $△ B M C$ 面积的最大值及相应点M的坐标；

(3)、如图2，该抛物线上是否存在点P，使得 $∠ A C O = ∠ B C P$ ？若存在，请求出所有点P的坐标；若不存在，请说明理由.

查看试题解析

平均数	中位数	众数	方差
8.8	8.7	8.7	0.11