山西省吕梁市交城县2021年中考数学二模试卷
试卷更新日期：2021-06-04 类型：中考模拟
一、单选题
-
1. 某地一天的最高气温是12℃，最低气温是-2℃，则该地这天的温差是（ ）A、﹣10℃ B、10℃ C、14℃ D、﹣14℃2. 下列图形中既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
3. 下列运算中正确的是（ ）A、 B、 C、 =2 D、﹣12=﹣24. 如图，AB是⊙O的直径，C，D两点在⊙O上，若∠C＝40°，则∠ABD的度数为（ ）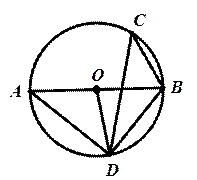
A、40° B、50° C、80° D、90°5. 一个暗箱里放有a个除颜色外完全相同的球，这a个球中红球只有4个，若每次将球搅匀后，任意摸出1个球记下颜色再放回暗箱，通过大量重复摸球实验后发现，摸到红球的频率稳定在20%附近，那么可以推算出a大约是（ ）
A、25 B、20 C、15 D、106. 如图，在△ABC中，D、E分别是边AB、BC上的点，且DE∥AC ， 若S△BDE：S△CDE＝1：3，则S△DOE：S△AOC的值为（ ）
A、 B、 C、 D、7. 某城市2018年底已有绿化面积500公顷，经过努力，绿化面积以相同的增长率逐年增加，到2020年底增加到605公顷．若按照这样的绿化速度，则该市2021年底绿化面积能达到（ ）A、657.5公顷 B、665.5公顷 C、673.5公顷 D、681.5公顷8. 将二次函数
的图象先向下平移1个单位，再向右平移3个单位，得到的图象与一次函数y=2x+b的图象有公共点，则实数b的取值范围是（ ） A、b＞8 B、b＞﹣8 C、b≥8 D、b≥﹣89. 已知“！”是一种数学运算符号，并且1！=1，2！=2×1=2，3！=3×2×1=6，4！=4×3×2×1=24，…，若公式 Cnm= （n＞m），则C125 =（ ）A、60 B、792 C、812 D、504010. 如图，以AB为直径的半圆圆心为O ， AB=10，折叠半圆使点A ， 点B都与圆心O重合，折痕分别为CD ， EF ， 连接DF ， 则图中阴影的面积为（ ）
A、 B、 C、 D、二、填空题
-
11. 不等式组 的解集为 ．12. 2020年10月23日在北京人民大会堂隆重举行了纪念中国人民志愿军抗美援朝出国作战70周年大会．在伟大的抗美援朝战争中，上甘岭战役是一场惨烈空前的战役．下图是利用网格画出的上甘岭战役的示意图.若建立适当的平面直角坐标系，表示上所里的点的坐标为（-1，2），表示注字洞的点的坐标为（0，3），则表示上甘岭的点（正好在网格点上）的坐标为 ．
13. 如图，正方形ABCD的边长为5，点A的坐标为（﹣4，0），点B在y轴上，若反比例函数y= （k≠0）的图象过点C，则该反比例函数的表达式为；
14.如图1，在某个盛水容器内，有一个小水杯，小水杯内有部分水，现在匀速持续地向小水杯内注水，注满小水杯后，继续注水，小水杯内水的高度y（cm）和注水时间x（s）之间的关系满足如图2中的图象，则至少需要 s能把小水杯注满．
15. 如图，折叠矩形纸片ABCD时，进行如下操作：①把△BCE翻折使点B落在DC边上的点F处，折痕为CE ， 点E在AB边上；②把纸片展开并铺平；③把△CDH翻折使点D落在线段AE上的点G处，折痕为CH ， 点H在AD边上．若 ，BC=6，则EG的长为 ．
三、解答题
-
16.(1)、计算：|2﹣ |﹣( )﹣2+tan60°+(﹣1)0；(2)、先化简，再求值： ÷( +1)，其中x= ﹣1．17. 已知：如图，四边形ABCD是⊙O的内接矩形，AB＝4，BC＝3，点E是劣弧 上的一点，连接AE ， DE ． 过点C作⊙O的切线交线段AE的延长线于点F ， 若∠CDE＝30°，求CF的长．
18. A、B与C三地依次在一条直线上.甲，乙两人同时分别从A，B两地沿直线匀速步行到C地，甲到达C地花了m分钟.设两人出发x(分钟)时，甲离B地的距离为y(米)，y与x的函数图象如图所示.
(1)、A地离C地的距离为米，m=；(2)、已知乙的步行速度是40米/分钟，设乙步行时与B地的距离为y(米)，直接写出y与x的函数关系式及自变量x的取值范围，并在图中画出此函数的图象；(3)、乙出发几分钟后两人在途中相遇？19. 随着通讯技术的迅猛发展，人与人之间的沟通方式更多样、便捷．某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷（每人必选且只选一种），在全校范围内随机调查了部分学生，将统计结果绘制了如下两幅不完整的统计图，请结合图中所给的信息解答下列问题：
(1)、这次统计共抽查了名学生，在扇形统计图中“QQ”的扇形圆心角的度数为；(2)、将条形统计图补充完整；(3)、某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系，请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率．20. 20． 歼-20（英文：Chengdu J-20，绰号：威龙，北约命名：Fire Fang）是我国自主研发的一款单座、双发动机并具备高隐身性、高态势感知、高机动性等能力的第五代战斗机．
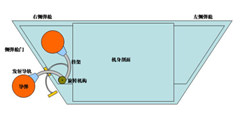
歼-20在机腹部位有一个主弹仓，机身两侧的起落架前方各有一个侧弹仓．歼-20的侧弹舱门为一片式结构，这个弹舱舱门向上开启，弹舱内滑轨的前端向外探出，使导弹头部伸出舱外，再直接点火发射．
如图是歼-20侧弹舱内部结构图，它的舱体横截面是等腰梯形ABCD ， AD//BC ， AB = CD ， BE⊥AD ， CF⊥AD ， 侧弹舱宽AE = 2.3米，舱底宽BC = 3.94米，舱顶与侧弹舱门的夹角∠A = 53°．
求：
(1)、侧弹舱门AB的长；(2)、舱顶AD与对角线BD的夹角的正切值．（结果精确到0.01，参考数据： ， ， ）．21. 某市在党中央实施“精准扶贫”政策的号召下，大力开展科技扶贫工作，帮助农民组建农副产品销售公司，某农副产品的年产量不超过100万件，该产品的生产费用y（万元）与年产量x（万件）之间的函数图象是顶点为原点的抛物线的一部分（如图①所示）；该产品的销售单价z（元/件）与年销售量x（万件）之间的函数图象是如图②所示的一条线段，生产出的产品都能在当年销售完，达到产销平衡，所获毛利润为w万元．（毛利润＝销售额﹣生产费用）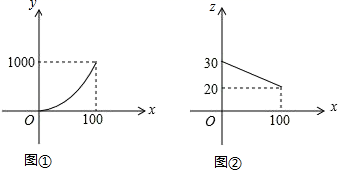
(1)、请直接写出y与x以及z与x之间的函数关系式；(2)、求w与x之间的函数关系式；并求年产量多少万件时，所获毛利润最大？最大毛利润是多少？(3)、由于受资金的影响，今年投入生产的费用不会超过360万元，今年最多可获得多少万元的毛利润？22. 综合与实践问题背景
在综合实践课上，同学们以“图形的平移与旋转”为主题开展数学活动，如图（1），先将一张等边三角形纸片ABC对折后剪开，得到两个互相重合的△ABD和△EFD ， 点E与点A重合，点B与点F重合，然后将△EFD绕点D顺时针旋转，使点F落在边AB上，如图（2），连接EC ．
(1)、操作发现判断四边形BFEC的形状，并说明理由；
(2)、实践探究聪聪提出疑问：若等边三角形的边长为8，将图（2）中的△EFD沿射线BC的方向平移a个单位长度，得到△E′F′D′ ， 连接BF′ ， CE′ ， 若四边形BF′E′C为菱形，如图（3），则a的值为多少？请你帮聪聪解决这个问题，求出a的值；
(3)、如果将（2）中聪聪所提问题的平移方向改为：沿射线CB的方向平移a个单位长度，其余条件都不变，则是否还存在四边形BF′E′C为菱形？若存在，直接写出平移距离a的值，若不存在，请说明理由；(4)、老师提出问题：请参照聪聪的思路，若等边三角形的边长为8，将图（2）中的△EFD在平面内进行一次平移，得到△E"F"D" ， 请在图（4）中画出平移后构造出的新图形，标明字母，说明平移及构图方法，写出你发现的一个结论，不必证明．23. 如图，已知抛物线经过原点o和x轴上一点A（4，0），抛物线顶点为E，它的对称轴与x轴交于点D．直线y=﹣2x﹣1经过抛物线上一点B（﹣2，m）且与y轴交于点C，与抛物线的对称轴交于点F．
(1)、求m的值及该抛物线对应的解析式；(2)、P（x，y）是抛物线上的一点，若S△ADP=S△ADC ， 求出所有符合条件的点P的坐标；(3)、点Q是平面内任意一点，点M从点F出发，沿对称轴向上以每秒1个单位长度的速度匀速运动，设点M的运动时间为t秒，是否能使以Q、A、E、M四点为顶点的四边形是菱形．若能，请直接写出点M的运动时间t的值；若不能，请说明理由．