四川省成都市青白江区2021年数学中考一诊试卷
试卷更新日期:2021-06-04 类型:中考模拟
一、单选题
-
1. 在下列各数中,最小的数是( )A、 B、 C、 D、2. 下列所给的图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 2020年前三个季度,青白江区实现地区生产总值约404亿元,同比增涨4.7%,高于全国4个百分点,增速居全市第三,请将404亿这个数据用科学记数法表示为( )A、 B、 C、 D、4. 下列运算正确的是 ( )A、 B、 C、 D、5. 如图,在 中, ,则 ( )
3. 2020年前三个季度,青白江区实现地区生产总值约404亿元,同比增涨4.7%,高于全国4个百分点,增速居全市第三,请将404亿这个数据用科学记数法表示为( )A、 B、 C、 D、4. 下列运算正确的是 ( )A、 B、 C、 D、5. 如图,在 中, ,则 ( )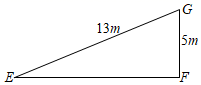 A、 B、 C、 D、6. 下列说法正确的是( )A、打开电视,它正在播天气预报是不可能事件 B、要考察一个班级中学生的视力情况适合用抽样调查 C、抛掷一枚均匀的硬币,正面朝上的概率是 ,若抛掷10次,就一定有5次正面朝上. D、甲、乙两人射中环数的方差分别为 , ,说明乙的射击成绩比甲稳定7. 如图所示的几何体是由一些相同大小的小正方体组合而成的,则这个几何体的三视图中,面积相等的是( )
A、 B、 C、 D、6. 下列说法正确的是( )A、打开电视,它正在播天气预报是不可能事件 B、要考察一个班级中学生的视力情况适合用抽样调查 C、抛掷一枚均匀的硬币,正面朝上的概率是 ,若抛掷10次,就一定有5次正面朝上. D、甲、乙两人射中环数的方差分别为 , ,说明乙的射击成绩比甲稳定7. 如图所示的几何体是由一些相同大小的小正方体组合而成的,则这个几何体的三视图中,面积相等的是( )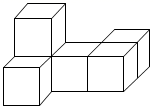 A、主视图和左视图 B、主视图和俯视图 C、左视图和俯视图 D、三种视图面积都相等8. 以下估算 的大小的数中,最接近的是( )A、3.9 B、4.1 C、4.5 D、5.19. 下列形状分别为正方形、矩形、正三角形、圆的边框,其中不一定是相似图形的是( )A、
A、主视图和左视图 B、主视图和俯视图 C、左视图和俯视图 D、三种视图面积都相等8. 以下估算 的大小的数中,最接近的是( )A、3.9 B、4.1 C、4.5 D、5.19. 下列形状分别为正方形、矩形、正三角形、圆的边框,其中不一定是相似图形的是( )A、 B、
B、 C、
C、 D、
D、 10. 对于函数 与 的图象的比较,下列说法不正确的是( )A、开口都向下 B、最大值都为0 C、对称轴相同 D、与x轴都只有一个交点
10. 对于函数 与 的图象的比较,下列说法不正确的是( )A、开口都向下 B、最大值都为0 C、对称轴相同 D、与x轴都只有一个交点二、填空题
-
11. 计算 的结果是.12. 一个多边形的内角和等于它的外角和的2倍,则这个多边形的边数是.13. 不等式组 的解集为.14. 已知点C是线段AB的黄金分割点,且AC>BC,若AB=2,则AC= .15. 已知: ,则 .16. 一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上.每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是.
 17. 如图,已知△ABC的三个顶点均在格点上,则cosA的值为.
17. 如图,已知△ABC的三个顶点均在格点上,则cosA的值为.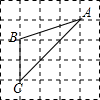 18. 如图,平行四边形 的顶点A在x轴的正半轴上,点 在对角线 上,反比例函数 的图象经过C、D两点,已知平行四边形 的面积是 ,则点B的坐标为.
18. 如图,平行四边形 的顶点A在x轴的正半轴上,点 在对角线 上,反比例函数 的图象经过C、D两点,已知平行四边形 的面积是 ,则点B的坐标为.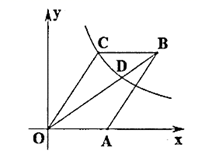 19. 如图,三角形纸片 ,点D是 边上一点,连接 ,把 沿着 翻折,得到 , 与 交于点G,连接 交 于点F.若 , , , 的面积为2,则点F到 的距离为.
19. 如图,三角形纸片 ,点D是 边上一点,连接 ,把 沿着 翻折,得到 , 与 交于点G,连接 交 于点F.若 , , , 的面积为2,则点F到 的距离为.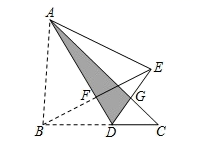
三、解答题
-
20.(1)、计算:(2)、先化简,再求值: ,其中 .21. 不解方程,判断下列关于x的方程根的情况:(1)、 ;(2)、 .22. 如图,A型、B型、C型三张矩形卡片的边长如图所示,将三张矩形卡片分别放入三个信封中,三个信封的外表完全相同;
 (1)、从这三个信封中随机抽取1个信封,则抽中A型矩形的概率为;(2)、先从这三个信封中随机抽取1个信封(不放回),再从余下的两个信封中随机抽取1个信封,求事件“两次抽中的矩形卡片能拼成(无重叠无缝隙)一个新矩形”发生的概率.(列表法或树状图)23. 如图,大楼AB的高为16米,远处有一塔CD,小李在楼底A处测得塔顶D处的仰角为60°,在楼顶B处测得塔顶D处的仰角为45°.其中A、C两点分别位于B、D两点正下方,且A、C两点在同一水平线上,求塔CD的高度.
(1)、从这三个信封中随机抽取1个信封,则抽中A型矩形的概率为;(2)、先从这三个信封中随机抽取1个信封(不放回),再从余下的两个信封中随机抽取1个信封,求事件“两次抽中的矩形卡片能拼成(无重叠无缝隙)一个新矩形”发生的概率.(列表法或树状图)23. 如图,大楼AB的高为16米,远处有一塔CD,小李在楼底A处测得塔顶D处的仰角为60°,在楼顶B处测得塔顶D处的仰角为45°.其中A、C两点分别位于B、D两点正下方,且A、C两点在同一水平线上,求塔CD的高度.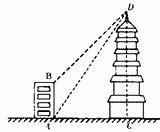 24. 如图,一次函数 的图象与反比例函数的图象相交于 两点.
24. 如图,一次函数 的图象与反比例函数的图象相交于 两点.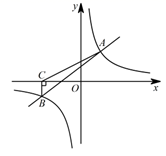 (1)、求一次函数与反比例函数的表达式;(2)、根据所给条件,请直接写出不等式 的解集: ;(3)、过点B作 轴,垂足为C,求 的面积 .25. 如图,在矩形 中,O是对角线 与 的交点, ,垂足为点E,已知 .
(1)、求一次函数与反比例函数的表达式;(2)、根据所给条件,请直接写出不等式 的解集: ;(3)、过点B作 轴,垂足为C,求 的面积 .25. 如图,在矩形 中,O是对角线 与 的交点, ,垂足为点E,已知 .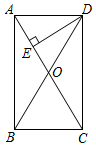 (1)、求证: ;(2)、若 ,求 的长.26. 某家具商场计划购进某种餐桌和餐椅,已知每张餐椅的进价比每张餐桌的进价便宜110元,餐桌零售价270元/张,餐椅零售价70元/张.已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.(1)、求该家具商场计划购进的餐桌、餐椅的进价分别为多少元?(2)、若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,售价500元/套,其余餐桌、餐椅以零售方式销售.请问该商场怎样进货,才能获得最大利润?最大利润是多少?27. 如图1,现有矩形纸片 , , .连接 ,将矩形 沿 剪开,得到 和 .保持 位置不变,将 从图1的位置开始,绕点B按逆时针方向旋转,旋转角为 .在 旋转过程中,连接 , .
(1)、求证: ;(2)、若 ,求 的长.26. 某家具商场计划购进某种餐桌和餐椅,已知每张餐椅的进价比每张餐桌的进价便宜110元,餐桌零售价270元/张,餐椅零售价70元/张.已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.(1)、求该家具商场计划购进的餐桌、餐椅的进价分别为多少元?(2)、若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,售价500元/套,其余餐桌、餐椅以零售方式销售.请问该商场怎样进货,才能获得最大利润?最大利润是多少?27. 如图1,现有矩形纸片 , , .连接 ,将矩形 沿 剪开,得到 和 .保持 位置不变,将 从图1的位置开始,绕点B按逆时针方向旋转,旋转角为 .在 旋转过程中,连接 , .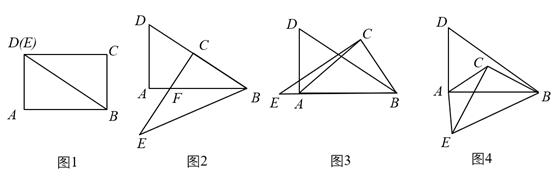 (1)、如图2,将图1中的 旋转到点C落在边 上时,边 与边 交于点F,则 的长为 ;(2)、如图3,将图1中的 旋转到当点E落在 延长线上时,求此时 的值;(3)、如图4,继续旋转图3中的 ,当 时停止旋转,求此时 的度数及 的面积;(4)、将图4中的 继续旋转,则在某一时刻 和 还能相等吗?如果不能,请说明理由,如果能,无需说明理由,请直接写出此时 的面积的值.28. 如图,二次函数y=ax2+bx+ 的图象经过A(﹣1,0),B(3,0),与y轴相交于点C.点P为第一象限的抛物线上的一个动点,过点P分别做BC和x轴的垂线,交BC于点E和F,交x轴于点M和N.
(1)、如图2,将图1中的 旋转到点C落在边 上时,边 与边 交于点F,则 的长为 ;(2)、如图3,将图1中的 旋转到当点E落在 延长线上时,求此时 的值;(3)、如图4,继续旋转图3中的 ,当 时停止旋转,求此时 的度数及 的面积;(4)、将图4中的 继续旋转,则在某一时刻 和 还能相等吗?如果不能,请说明理由,如果能,无需说明理由,请直接写出此时 的面积的值.28. 如图,二次函数y=ax2+bx+ 的图象经过A(﹣1,0),B(3,0),与y轴相交于点C.点P为第一象限的抛物线上的一个动点,过点P分别做BC和x轴的垂线,交BC于点E和F,交x轴于点M和N.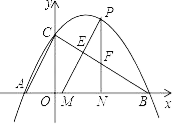 (1)、求这个二次函数的解析式;(2)、求线段PE最大值,并求出线段PE最大时点P的坐标;(3)、若S△PMN=3S△PEF时,求出点P的坐标.
(1)、求这个二次函数的解析式;(2)、求线段PE最大值,并求出线段PE最大时点P的坐标;(3)、若S△PMN=3S△PEF时,求出点P的坐标.