浙江省宁波市海曙区2021年数学中考模拟试卷（5月）

试卷更新日期：2021-06-04 类型：中考模拟

进入出卷网下载

一、单选题

1. 数1，0， $- \frac{2}{3}$ ， $| - 2 |$ 中最大的是（　）

A、1 B、0 C、 $- \frac{2}{3}$ D、 $| - 2 |$

查看试题解析
2. 下列计算正确的是（）

A、 $a^{5} \div a = a^{4} (a \neq 0)$ B、 $(a + 2) (a - 2) = a^{2} - 2$ C、 $(a + 1) (a - 2) = a^{2} + a - 2$ D、 $3 a^{2} - a^{2} = 3$

查看试题解析
3. 宁波市“十四五”规划中指出，到二〇二五年，经济总量和发展质量跃上新台阶，全市生产总值达到1.7万亿元，其中1.7万亿元用科学记数法表示为（）

A、 $17 \times 10^{11}$ 元 B、 $1.7 \times 10^{11}$ 元 C、 $1.7 \times 10^{12}$ 元 D、 $0.17 \times 10^{13}$ 元

查看试题解析
4. 能说明命题“当a为实数时，则 $a^{2} \geq a$ ”是假命题的反例是（）

A、 $a = 2$ B、 $a = - 1$ C、 $a = - 0.5$ D、 $a = 0.5$

查看试题解析
5. 如图所示的几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
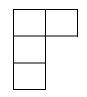6. 一组数据1，2，3，4，5的方差是a，若增加一个数据9，则增加后6个数据的方差为b，则a与b的大小关系是（）

A、a < b B、a = b C、a > b D、不能确定

查看试题解析
7. 如图为一节楼梯的示意图，BC⊥AC，∠BAC=α，AC=6米。现要在楼梯上铺一块地毯，楼梯宽度为1米，则地毯的面积至少需要（）平方米。

A、6tanα+6 B、 $\frac{6}{\tan α}$ +6 C、 $\frac{6}{\cos α}$ D、 $\frac{6}{\sin α}$

查看试题解析
8. 在平面直角坐标系中，点 $P (m, 2 m - 2)$ ，则点P不可能在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
9. 如图，⊙O经过菱形ABCD的顶点B，C，且与边AD相切于点E.若AE＝1，ED＝5，则⊙O的半径为（）

A、 $4 \sqrt{2}$ B、 $5 \sqrt{2}$ C、 $\frac{41}{16} \sqrt{2}$ D、 $\frac{41}{8} \sqrt{2}$

查看试题解析
10. 如图，在Rt△ABC中，∠BAC=90^° ，以其三边为边分别向外作正方形，延长EC，DB分别交GF，AH于点N，K，连结KN交AG于点M，若S₁-S₂=2，AC=4，则AB的长为（）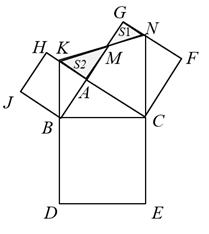

A、2 B、 $\sqrt{2}$ C、 $2 \sqrt{2}$ D、 $\frac{7}{3}$

查看试题解析

二、填空题

11. $27$ 的立方根是．

查看试题解析
12. 因式分解： $4 x^{2} - 16$ =.

查看试题解析
13. 一张圆形纸片裁剪后正好能做三个一样的无底圆锥纸帽（无余料，接缝不计），若圆锥的高为4cm，则每个圆锥的侧面积是.

查看试题解析

14. 为落实省新课改精神，宁波市各校都开设了“知识拓展类”、“体艺特长类”、“实践活动类”三类拓展课程.下列数据是某校八年级学生“体艺特长类”课程的参与情况：

课程（类别）	艺术修养	快乐足球	魅力舞蹈	笔墨载古	美丽瑜伽	精英篮球
人数（人）	20	24	18	23	18	16

则这组数据的中位数为人.

查看试题解析

15. 如图，已知在△ABC中，∠C=60°，⊙O是△ABC的外接圆，过点A、B分别作⊙O的切线，两切线交于点P，若⊙O的半径为1，则△PAB的周长为 .

查看试题解析
16. 如图，已知双曲线 $y = \frac{12}{x} (x < 0)$ 和 $y = \frac{k}{x} (x > 0)$ ，直线 $O A$ 与双曲线 $y = \frac{12}{x}$ 交于点A，将直线 $O A$ 向下平移与双曲线 $y = \frac{12}{x}$ 交于点B，与y轴交于点P，与双曲线 $y = \frac{k}{x}$ 交于点C， $S_{△ A B C} = 6$ ， $B P ： C P = 2 ： 1$ ，则k的值为.

查看试题解析

三、解答题

17.

(1)、计算： ${(- 2)}^{- 1} - | - \sqrt{4} | + \sin 30^{°} + {(\sqrt{2} - \sqrt{3})}^{0}$

(2)、解方程： $\frac{x - 2}{x + 2} - \frac{2}{x - 2} = 1$

查看试题解析
18. 如图，∠ACB在6×6方格中，点A，B，C在格点上，按要求画图：

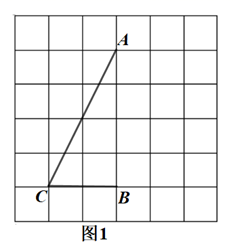
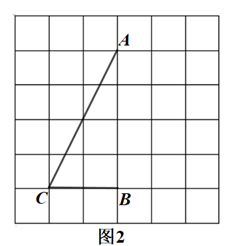(1)、在图1中画出∠APB，使得∠APB＝∠ACB，点P为格点.

(2)、在图2中画出∠AMB，使得∠AMB+∠ACB＝180°，点M为格点.

查看试题解析
19. 某校将九年级学生英语人机对话的一次模拟测试成绩分为A，B，C，D四个等级，现随机抽取一部分学生的成绩进行统计，并绘制了下列两幅统计图（部分信息未给出）：

(1)、求扇形统计图中C等级所对应的圆心角的度数；

(2)、请将条形统计图补充完整；

(3)、记A或B等级的成绩为优秀，若该校九年级学生共600人，请你估计成绩为优秀的学生有多少人？

查看试题解析
20. 如图1，一扇窗户打开后可以用窗钩AB将其固定，窗钩的一个端点A固定在窗户底边OE上，且与转轴底端O之间的距离为20cm，窗钩的另一个端点B可在窗框边上的滑槽OF上移动，滑槽OF的长度为17cm，AB、BO、AO构成一个三角形．当窗钩端点B与点O之间的距离是7cm的位置时（如图2），窗户打开的角∠AOB的度数为37°．

(1)、求钩AB的长度（精确到1cm）；

(2)、现需要将窗户打开的角∠AOB的度数调整到45°时，求此时窗钩端点B与点O之间的距离（精确到1cm）．（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75， $\sqrt{2}$ ≈1.4）

查看试题解析
21. 如图，在Rt△ACB中，∠ACB＝90°，点D为BC延长线上一点，以BD为直径作半圆O分别交AB，AC于点G，E，点E为 $\overset{⌢}{D G}$ 的中点，过点E作⊙O的切线交AB于点F.

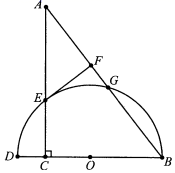(1)、求证：∠AEF＝∠ABC.

(2)、若sinA＝ $\frac{2}{3}$ ，FG＝1，求AC的长.

查看试题解析
22. 某款轿车每行驶100千米的耗油量y升与其行驶速度x千米/小时之间的函数关系图象如图所示，其中线段AB的表达式为 $y = - \frac{1}{25} x + 13 (25 \leq x \leq 100)$ ，点C的坐标为（140，14），即行驶速度为140千米/小时时该轿车每行驶100千米的耗油量是14升.

(1)、求线段BC的表达式；

(2)、如果从甲地到乙地全程为260千米，其中有60千米限速50千米/小时的省道和200千米限速120千米/小时的高速公路，那么在不考虑其他因素的情况下，这款轿车从甲地行驶到乙地至少需要耗油多少升？

查看试题解析
23. 如果抛物线C₁： $y = a x^{2} + b x + c$ 与抛物线C₂： $y = - a x^{2} + d x + e$ 的开口方向相反，顶点相同，我们称抛物线C₂是C₁的“对顶”抛物线.

(1)、求抛物线 $y = x^{2} - 4 x + 7$ 的“对顶”抛物线的表达式；

(2)、将抛物线 $y = x^{2} - 4 x + 7$ 的“对顶”抛物线沿其对称轴平移，使所得抛物线与原抛物线 $y = x^{2} - 4 x + 7$ 形成两个交点M、N，记平移前后两抛物线的顶点分别为A、B，当四边形AMBN是正方形时，求正方形AMBN的面积.

(3)、某同学在探究“对顶”抛物线时发现：如果抛物线C₁与C₂的顶点位于x轴上，那么系数b与d，c与e之间的关系是确定的，请写出它们之间的关系.

查看试题解析
24. 如图，在Rt△ABC中，∠ABC=90°，AB=1，AC= $\sqrt{5}$ ，点M是线段CA上的动点(M不与点A、C重合)，作△ABM的外接圆⊙O，过点A作AN $//$ BC，交⊙O于N点.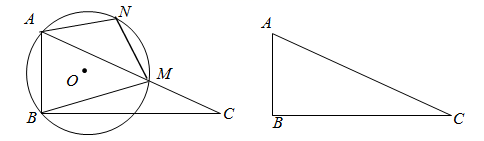

(1)、tanC的值为.

(2)、若△ANM∽△CMB(其中点A与点C对应，点M与点B对应)，求AM的长.

(3)、①若△AMN为等腰三角形，求线段MC的长度.
②若S_△BMN=S_△BMC ，请直接写出此时△BMN的面积 ▲ .

查看试题解析