江西省赣州市石城县2021年中考数学一模试卷

试卷更新日期：2021-06-04 类型：中考模拟

进入出卷网下载

一、单选题

1. ﹣3的绝对值是（）

A、﹣3 B、3 C、- $\frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
2. 下列四个算式中正确的是（）

A、a²＋a³＝a⁵ B、（﹣a²）³＝a⁶ C、a²•a³＝a⁶ D、a³÷a²＝a

查看试题解析
3. 如图的两个几何体分别由7个和6个相同的小正方体搭成，比较两个几何体的三视图，正确的是（）

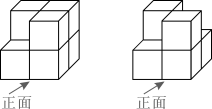A、仅主视图不同 B、仅俯视图不同 C、仅左视图不同 D、主视图、左视图和俯视图都相同

查看试题解析
4. 我县正在创建国家全域旅游示范区，区域内的八卦脑、通天寨、花乐园、九寨温泉、九叠泉都深受游客喜爱．某班同学分小组到以上五个地方进行“我爱家乡”主题研学旅行，人数分别为：12，5，11，5，7（单位：人），这组数据的众数和中位数分别是（）

A、5人，7人 B、5人，11人 C、5人，12人 D、7人，11人

查看试题解析
5. 如图是由三个全等的菱形拼接而成的图形，若平移其中一个菱形，与其他两个菱形重新拼接（无覆盖，有公共顶点），并使拼接成的图形为轴对称图形，则平移的方式共有（）

A、5种 B、6种 C、7种 D、8种

查看试题解析
6. 已知P₁（x₁ ， y₁），P₂（x₂ ， y₂）是抛物线y＝ax²﹣2ax上的点，下列命题正确的是（）

A、若|x₁﹣1|＞|x₂﹣1|，则y₁＞y₂ B、若|x₁﹣1|＞|x₂﹣1|，则y₁＜y₂ C、若|x₁﹣1|＝|x₂﹣1|，则y₁＝y₂ D、若y₁＝y₂ ，则x₁＝x₂

查看试题解析

二、填空题

7. 因式分解： $7 a^{2} - 7 b^{2}$ = ．

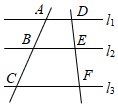
查看试题解析
8. 如图，直线l₁∥l₂∥l₃ ，直线AC和DF被l₁ ， l₂ ， l₃所截，AB＝5，BC＝6，EF＝4，则DE的长为．

查看试题解析
9. 若x₁ ， x₂是方程x²﹣4x﹣2020＝0的两个实数根，则代数式x₁²﹣2x₁+2x₂的值等于.

查看试题解析
10. 《孙子算经》中有一道题：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”译文大致是：“用一根绳子去量一根木条，绳子剩余4.5尺；将绳子对折再量木条，木条剩余1尺，问木条长多少尺？”如果设木条长x尺，绳子长y尺，可列方程组为；

查看试题解析
11. 如图，在矩形ABCD中，AB=1，AD= $\sqrt{3}$ ，P为AD上一个动点，连接BP，线段BA与线段BQ关于BP所在的直线对称，连接PQ，当点P从点A运动到点D时，线段PQ在平面内扫过的面积为.

查看试题解析
12. 如图，在矩形 $A B C D$ 中， $A B = 6$ ， $B C = 8$ ，对角线 $A C ， B D$ 相交于点O，点P为边 $A D$ 上一动点，连接 $O P$ ，以 $O P$ 为折痕，将 $△ A O P$ 折叠，点A的对应点为点E，线段 $P E$ 与 $O D$ 相交于点F.若 $△ P D F$ 为直角三角形，则 $D P$ 的长.

查看试题解析

三、解答题

13.

(1)、解不等式： $\frac{2 x - 1}{3} - \frac{9 x + 2}{6}$ ≤ $1$

(2)、如图，A ， E两点在线段DB上，EF＝BC ， DF＝AC ， DA＝EB ．求证：EF∥BC ．

查看试题解析
14. 先化简，再求值： $(1 - \frac{1}{x + 1}) \div \frac{x^{2}}{x^{2} - 1}$ ，其中x=2020．

查看试题解析
15. 2021年我省全面推行初中学业水平考试改革，为了解各市九年级学生复习备考情况，省教育厅准备对各市进行一次实地调研活动，调研的对象初步确定从A市、B市、C市、D市、E市中随机抽签选取．

(1)、若这次调研准备选取一个市，则恰好抽到A市的概率是．

(2)、若这次调研准备选取两个市，请用列表或画树状图的方法表示出所有可能，并求出所选取的两个市恰好是A市和B市的概率．

查看试题解析
16. 如图，四边形ABCD是平行四边形，AD与圆相切，请在下图中，仅用无刻度的直尺按要求画图．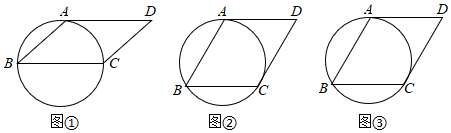

⑴如图①，若BC是圆的直径，画出平行四边形ABCD的边CD上的高；

⑵如图②，若CD与圆相切，画出平行四边形ABCD的边AD上的高CE；

⑶如图③，若CD与圆相切，画出平行四边形ABCD的边BC上的高AF ．

查看试题解析
17. 九年级学生到距离学校6千米的百花公园去春游，一部分学生步行前往，20分钟后另一部分学生骑自行车前往，设 $x$ （分钟）为步行前往的学生离开学校所走的时间，步行学生走的路程为 $y_{1}$ 千米，骑自行车学生骑行的路程为 $y_{2}$ 千米， $y_{1} 、 y_{2}$ 关于 $x$ 的函数图象如图所示.

(1)、求 $y_{2}$ 关于 $x$ 的函数解析式；

(2)、步行的学生和骑自行车的学生谁先到达百花公园，先到了几分钟？

查看试题解析

18. 为增强学生环保意识．实施垃圾分类管理．某中学举行了“垃圾分类知识竞赛"并随机抽取了部分学生的竞赛成绩绘制了如下不完整的统计图表．

知识竞赛成馈频数分布表

组别	成绩（分数）	人数
$A$	$95 \leq x < 100$	$300$
$B$	$90 \leq x < 95$	$a$
$C$	$85 \leq x < 90$	$150$
$D$	$80 \leq x < 85$	$200$
$E$	$75 \leq x < 80$	$b$

根据所给信息，解答下列问题．

(1)、a= ，

b =

；

(2)、请求出扇形统计图中C组所在扇形的圆心角的度数；

(3)、补全知识竞赛成绩频数分布直方图；

(4)、已知该中学有

3500

名学生，请估算该中学学生知识竞赛成绩低于

80

分的人数．

查看试题解析

19. 如今，不少人在购买家具时追求简约大气的风格，图1所示的是一款非常畅销的简约落地收纳镜，其支架的形状固定不变，镜面可随意调节，图2所示的是其侧面示意图，其中 $O D$ 为镜面， $E F$ 为放置物品的收纳架， $A B ， A C$ 为等长的支架， $B C$ 为水平地面，已知 $O A = 44 c m ， O D = 120 c m ， B D = 40 c m$ ， $∠ A B C = 75 °$ ．(结果精确到 $1 c m$ ．参考数据： $s i n 75 ° \approx 0.97 ， c o s 75 ° \approx 0.26 ， t a n 75 ° \approx 3.73 ， \sqrt{2} \approx 1.41 ， \sqrt{3} \approx 1.73$ )

(1)、求支架顶点A到地面 $B C$ 的距离．

(2)、如图3，将镜面顺时针旋转15°求此时收纳镜顶部端点O到地面 $B C$ 的距离．

查看试题解析
20. 如图，正比例函数y＝kx（k≠0）的图象与反比例函数y＝﹣ $\frac{8}{x}$ 的图象交于点A(n，2)和点B.

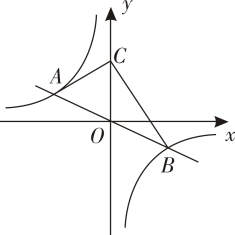(1)、n＝， k＝；

(2)、点C在y轴正半轴上.∠ACB＝90°，求点C的坐标；

(3)、点P（m，0）在x轴上，∠APB为锐角，直接写出m的取值范围.

查看试题解析
21. 如图，在△ABC的边BC上取一点O ，以O为圆心，OC为半径画⊙O ， ⊙O与边AB相切于点D ， AC＝AD ，连接OA交⊙O于点E ，连接CE ，并延长交线段AB于点F ．

(1)、求证：AC是⊙O的切线；

(2)、若AB＝10，tanB $= \frac{4}{3}$ ，求⊙O的半径；

(3)、若F是AB的中点，试探究BD＋CE与AF的数量关系并说明理由．

查看试题解析
22. 规定：对于抛物线y＝ax²＋bx＋c ，与该抛物线关于点M（m ， n）（m＞0，n≥0）成中心对称的抛物线为y′，我们称抛物线y′为抛物线y的发散抛物线，点M称为发散中心．已知抛物线y₀＝mx²＋4x＋3经过点（﹣1，0），顶点为A ，抛物线y₁与该抛物线关于点（1，0）成中心对称．

(1)、m＝，点A的坐标是，抛物线y₁的解析式是．

(2)、对于抛物线y₀＝mx²＋4x＋3，如图，现分别以y₁的顶点A₁为发散中心，得抛物线y₂；再以抛物线y₂的顶点A₂为发散中心，得抛物线y₃ ， …，以此类推．
①求抛物线y₀＝mx²＋4x＋3以A₁为发散中心得到的抛物线y₂的解析式；

②求发散抛物线y₄的发散中心A₃的坐标；

③若发散抛物线y_n的顶点A_n的坐标为（3×2ⁿ^﹣2 ， 2ⁿ^﹣1），请直接写出A_nA_n_﹣1的长度（用含n的式子表示）．

查看试题解析
23. 定义：三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角．

(1)、如图1，∠E是△ABC中∠A的遥望角，若∠A＝α，请用含α的代数式表示∠E．

(2)、如图2，四边形ABCD内接于⊙O， $\hat{A D}$ ＝ $\hat{B D}$ ，四边形ABCD的外角平分线DF交⊙O于点F，连结BF并延长交CD的延长线于点E．求证：∠BEC是△ABC中∠BAC的遥望角．

(3)、如图3，在（2）的条件下，连结AE，AF，若AC是⊙O的直径．
①求∠AED的度数；

②若AB＝8，CD＝5，求△DEF的面积．

查看试题解析