黑龙江省大庆市肇源县2021年中考数学一模试卷

试卷更新日期：2021-06-04 类型：中考模拟

进入出卷网下载

一、单选题

1. 2020年6月23日，中国第55颗北斗导航卫星成功发射，顺利完成全球组网．其中支持北斗三号新信号的22纳米工艺射频基带一体化导航定位芯片，已实现规模化应用，22纳米=0.000000022米，将0.000000022用科学记数法表示为（）

A、22×10⁸ B、2.2×10^-8 C、0.22×10^-7 D、22×10^-9

查看试题解析
2. 下列运算，正确的是（）

A、 $2 x + 3 y = 5 x y$ B、 ${(x - 3)}^{2} = x^{2} - 9$ C、 ${(x y^{2})}^{2} = x^{2} y^{4}$ D、 $x^{6} \div x^{3} = x^{2}$

查看试题解析
3. 下面四个化学仪器示意图中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列说法正确的有（）个
①同位角相等；

②一条直线有无数条平行线；

③在同一平面内，两条不相交的线段是平行线；

④如果 $a / / b$ ， $b / / c$ ，则 $a / / c$ ；

⑤过一点有且只有一条直线与已知直线平行．

A、2个 B、3个 C、4个 D、5个

查看试题解析
5. 一组数据4，4，x，8，8有唯一的众数，则这组数据的平均数是（）

A、 $\frac{28}{5}$ B、 $\frac{32}{5}$ 或5 C、 $\frac{28}{5}$ 或 $\frac{32}{5}$ D、5

查看试题解析
6. 已知关于x的分式方程 $\frac{x}{x - 2} - 4 = \frac{k}{2 - x}$ 的解为正数，则k的取值范围是（）

A、 $- 8 < k < 0$ B、 $k > - 8$ 且 $k \neq - 2$ C、 $k > - 8$ 且 $k \neq 2$ D、 $k < 4$ 且 $k \neq - 2$

查看试题解析
7. 如图，菱形ABCD的对角线AC、BD相交于点O ，过点D作DH⊥AB于点H ，连接OH ，若OA=6，S_菱形ABCD=48，则OH的长为（）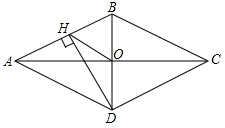

A、4 B、8 C、 $\sqrt{13}$ D、6

查看试题解析
8. 如图，点A在反比例函数 $y_{1} = \frac{18}{x} (x > 0)$ 的图象上，过点A作 $A B ⊥ x$ 轴，垂足为B，交反比例函数 $y_{2} = \frac{6}{x} (x > 0)$ 的图象于点C．P为y轴上一点，连接 $P A$ ， $P C$ ．则 $△ A P C$ 的面积为（）

A、5 B、6 C、11 D、12

查看试题解析
9. 如图，在菱形纸片ABCD中，AB=2，∠A=60°，将菱形纸片翻折，使点A落在CD的中点E处，折痕为FG，点F，G分别在边AB，AD上，则EF的长为（）

A、 $\frac{7}{4}$ B、 $\frac{9}{5}$ C、 $\frac{19}{10}$ D、 $\frac{7}{6} \sqrt{3}$

查看试题解析
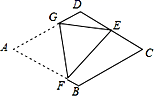10. 二次函数y＝ax²+bx+c(a≠0)的大致图象如图所示，顶点坐标为(﹣2，﹣9a)，下列结论：①abc＞0；②4a+2b+c＞0；③5a﹣b+c＝0；④若方程a(x+5)(x﹣1)＝﹣1有两个根x₁和x₂ ，且x₁＜x₂ ，则﹣5＜x₁＜x₂＜1；⑤若方程|ax²+bx+c|＝2有四个根，则这四个根的和为﹣4．其中正确的结论有（）

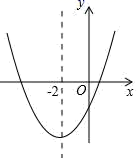A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

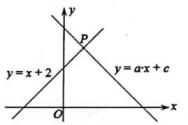
11. 函数y＝ $\frac{x - 1}{x + 5}$ 中，自变量x的取值范围是．

查看试题解析
12. 分解因式：（p+1）（p﹣4）+3p= ．

查看试题解析
13. 如图，直角坐标系中直线y=x+2和直线y=ax+c相交于点P(m，3)，则方程组 ${\begin{cases} y = x + 2 \\ y = a x + c \end{cases}$ 的解为。

查看试题解析
14. 为考察甲、乙两种油菜的长势，分别从中抽取20株测其高度进行统计分析，结果如下： $\bar{x}$ _甲＝1.29m， $\bar{x}$ _乙＝1.29m，s_甲²＝1.6米²、s_乙²＝4.8米² ，则油菜花长势比较整齐的是．

查看试题解析
15. 如图，由等圆组成的一组图中，第1个图由1个圆组成，第2个图由5个圆组成，第3个图由11个圆组成，…，按照这样的规律排列下去，则第9个图形由个圆组成，

查看试题解析
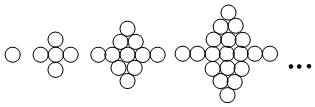16. 如图，已知矩形OABC与矩形FEDO是位似图形，P是位似中心，若点A的坐标为（0，6），点E的坐标为（2，3），则点B的坐标为．

查看试题解析
17. 如图，正方形OABC的边长为8，A、C两点分别位于x轴、y轴上，点P在AB上，CP交OB于点Q，函数y＝ $\frac{k}{x}$ 的图像经过点Q，若S_△_BPQ＝ $\frac{1}{9}$ S_△_OQC ，则k的值为．

查看试题解析
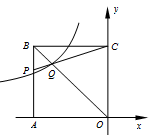18. 如图，在边长为3的等边△ABC中，点D在AC上，且CD＝1，点E在AB上（不与点A、B重合），连接DE，把△ADE沿DE折叠，当点A的对应点F落在等边△ABC的边上时，AE的长为.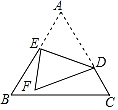

查看试题解析

三、解答题

19. 计算： $\sqrt{8} \times \sqrt{2} - 2 \sin 60 ° - | \sqrt{3} - 2 | + {(\frac{1}{2})}^{- 1}$ ．

查看试题解析
20. 先化简，再求值： $\frac{x^{2}}{x^{2} - 1} \div (\frac{1}{x - 1} + 1)$ ，其中 $x$ 为整数且满足不等式组 ${\begin{array}{l} x - 1 > 1, \\ 5 - 2 x \geq - 2. \end{array}$

查看试题解析
21. 解方程： $\frac{x}{x - 1} = \frac{4}{x^{2} - 1} + 1$

查看试题解析
22. 某区域平面示意图如图，点O在河的一侧，AC和BC表示两条互相垂直的公路．甲勘测员在A处测得点O位于北偏东45°，乙勘测员在B处测得点O位于南偏西73.7°，测得AC=840m，BC=500m．请求出点O到BC的距离．
参考数据：sin73.7°≈ $\frac{24}{25}$ ，cos73.7°≈ $\frac{7}{25}$ ，tan73.7°≈ $\frac{24}{7}$

查看试题解析
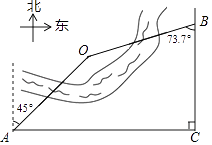23. “春节”是我国最重要的传统佳节，北方地区历来有“吃饺子”的习俗．某饺子厂为了解市民对去年销售较好的猪肉大葱馅、韭菜鸡蛋馅、香菇馅、三鲜馅（分别用A、B、C、D表示）这四种不同口味饺子的喜爱情况，在节前对某居民区市民进行了抽样调查，并将调查情况绘制成两幅统计图（尚不完整）．

请根据所给信息回答：

(1)、本次参加抽样调查的居民有人；

(2)、将两幅不完整的统计图补充完整；

(3)、若居民区有8000人，请估计爱吃D种饺子的人数；

(4)、若有外形完全相同的4盘饺子，分别装有A、B、C、D这4类饺子，老张从中挑了2盘．求他同时吃到A、B两种饺子的概率（用树状图或者列表分析）．

查看试题解析
24. 如图，一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{m}{x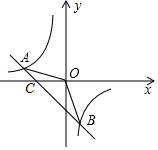}$ 的图象交于 $A (- 2 ， 1)$ ， $B (1 ， n)$ 两点．

(1)、求一次函数与反比例函数的表达式；

(2)、求 $△ A O B$ 的面积；

(3)、根据所给条件，请直接写出不等式 $k x + b < \frac{m}{x}$ 的解集．

查看试题解析
25. 如图，在四边形ABCD中，∠BAC＝90°，E是BC的中点，AD∥BC，AE∥DC，EF⊥CD于点F.

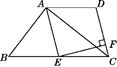(1)、求证：四边形AECD是菱形；

(2)、若AB＝6，BC＝10，求EF的长.

查看试题解析
26. 工艺商场按标价销售某种工艺品时，每件可获利45元，按标价的八五折销售共工艺品8件与将标价降低35元销售该工艺品12件所获利润相等．

(1)、该工艺品每件的进价、标价分别是多少元？

(2)、若每件工艺品按（1）中求得的进价进货，标价售出，工艺商场每天可售出该工艺品100件，若每件工艺品降价1元，则每天可售出该工艺品4件，如果既要每天要获得的利润4800元，又要使消费者得到实惠，问每件工艺品降价多少元出售？

(3)、请商场如何定价可以使每天获得最高利润？

查看试题解析
27. 已知：如图，⊙O的直径AB垂直于弦CD ，过点C的切线与直径AB的延长线相交于点P ，连接PD ．

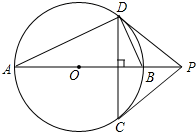(1)、求证：PD是⊙O的切线．

(2)、求证： $P D^{2} = P B \cdot P A$ ．

(3)、若PD=4， $\tan ∠ C D B = \frac{1}{2}$ ，求直径AB的长．

查看试题解析
28. 如图，直线y＝x+2与抛物线y＝ax²+bx+6相交于A( $\frac{1}{2}$ ， $\frac{5}{2}$ )和B(4，m)，直线AB交x轴于点E，点P是线段AB上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．

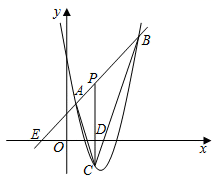(1)、求抛物线的解析式.

(2)、连结AC、BC，是否存在一点P，使△ABC的面积等于14？若存在，请求出此时点P的坐标；若不存在，请说明理由.

(3)、若△PAC与△PDE相似，求点P的坐标.

查看试题解析