河北省唐山市古冶区2021年中考数学一模试卷
试卷更新日期:2021-06-04 类型:中考模拟
一、单选题
-
1. 若a与1互为相反数,那么 ( )A、 B、0 C、1 D、2. 如图,在数轴上,点A表示的数是 ,将点A沿数轴正方向向右移动4个单位长度得到点P,则点P表示的数是( )
 A、4 B、3 C、2 D、3. 下图均由正六边形与两条对角线所组成,既是轴对称图形又是中心对称图形的是( )A、
A、4 B、3 C、2 D、3. 下图均由正六边形与两条对角线所组成,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 2019年全国共享单车投放量达23000000辆,将23000000用科学记数法表示为( )A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 将一副三角板( , )按如图所示方式摆放,点F在 的延长线上,若 ,则 ( )
4. 2019年全国共享单车投放量达23000000辆,将23000000用科学记数法表示为( )A、 B、 C、 D、5. 下列运算正确的是( )A、 B、 C、 D、6. 将一副三角板( , )按如图所示方式摆放,点F在 的延长线上,若 ,则 ( )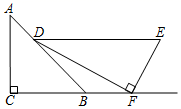 A、 B、 C、 D、7. 如图,A处在B处的北偏东45°方向,A处在C处的北偏西15°方向,则∠BAC等于( )
A、 B、 C、 D、7. 如图,A处在B处的北偏东45°方向,A处在C处的北偏西15°方向,则∠BAC等于( ) A、30° B、45° C、50° D、608. 点 经过某种图形变化后得到点 ,这种图形变化可以是( )A、关于 轴对称 B、关于 轴对称 C、绕原点逆时针旋转 D、绕原点顺时针旋转9. 数学老师在课堂上给同学们布置了10个填空题作为课堂练习,并将全班同学的答题情况绘制成条形统计图.由图可知,全班同学答对题数的众数为( )
A、30° B、45° C、50° D、608. 点 经过某种图形变化后得到点 ,这种图形变化可以是( )A、关于 轴对称 B、关于 轴对称 C、绕原点逆时针旋转 D、绕原点顺时针旋转9. 数学老师在课堂上给同学们布置了10个填空题作为课堂练习,并将全班同学的答题情况绘制成条形统计图.由图可知,全班同学答对题数的众数为( ) A、7 B、8 C、9 D、1010. 当 时,关于x的一元二次方程 根的情况是( )A、有两个相等的实数根 B、有两个不等的实数根 C、有一个实数根 D、没有实数根11. 以下是小明同学解方程 的过程:
A、7 B、8 C、9 D、1010. 当 时,关于x的一元二次方程 根的情况是( )A、有两个相等的实数根 B、有两个不等的实数根 C、有一个实数根 D、没有实数根11. 以下是小明同学解方程 的过程:解:方程两边同时乘以 ,得
,第一步
即 ,第二步
解得, ,第三步
检验:当 时, ,
所以原方程的解是 .第四步
针对以上解题过程,下列说法正确的是( )
A、从第一步开始有错 B、从第二步开始有错 C、从第三步开始有错 D、完全符合题意12. 我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是100,小正方形面积是20,则 ( ) A、 B、 C、 D、13. 如图,在 中,按以下步骤作图:①分别以B,C为圆心,大于 的长为半径作弧,两弧相交于两点M,N;②作直线 交 于点D,连接 .若 , ,则 ( )
A、 B、 C、 D、13. 如图,在 中,按以下步骤作图:①分别以B,C为圆心,大于 的长为半径作弧,两弧相交于两点M,N;②作直线 交 于点D,连接 .若 , ,则 ( ) A、 B、 C、 D、14. 如图,点O为矩形 的对称中心,点E从点A出发沿 向点B运动到点B停止,延长 交 于点F,则四边形 形状的变化依次为( )
A、 B、 C、 D、14. 如图,点O为矩形 的对称中心,点E从点A出发沿 向点B运动到点B停止,延长 交 于点F,则四边形 形状的变化依次为( ) A、平行四边形→正方形→平行四边形→矩形 B、平行四边形→菱形→平行四边形→矩形 C、平行四边形→正方形-菱形→矩形 D、正方形→菱形→平行四边形→矩形15. 关于抛物线 ,有以下结论:①当 时,抛物线过原点;②抛物线必过点 ;③顶点的纵坐标最大值为1;④若当 时, ,当 时,y随x的增大而减小,则b的取值范围是 .错误结论的序号是( )A、① B、② C、③ D、④16. 如图,点A , B的坐标分别为 ,点C为坐标平面内一点, ,点M为线段 的中点,连接 ,则 的最大值为( )
A、平行四边形→正方形→平行四边形→矩形 B、平行四边形→菱形→平行四边形→矩形 C、平行四边形→正方形-菱形→矩形 D、正方形→菱形→平行四边形→矩形15. 关于抛物线 ,有以下结论:①当 时,抛物线过原点;②抛物线必过点 ;③顶点的纵坐标最大值为1;④若当 时, ,当 时,y随x的增大而减小,则b的取值范围是 .错误结论的序号是( )A、① B、② C、③ D、④16. 如图,点A , B的坐标分别为 ,点C为坐标平面内一点, ,点M为线段 的中点,连接 ,则 的最大值为( )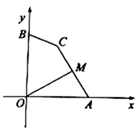 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
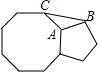
17. 分解因式: .18. 如图,正八边形和正五边形按如图方式拼接在一起,则 .
 19. 在平面直角坐标系中,二次函数 (k为常数)与反比例函数 ( )的图象如图所示, , 是反比例函数图象上的两点,记P、Q两点间的部分为 ,
19. 在平面直角坐标系中,二次函数 (k为常数)与反比例函数 ( )的图象如图所示, , 是反比例函数图象上的两点,记P、Q两点间的部分为 , (1)、当 时,二次函数的对称轴为;(2)、 ;(3)、若二次函数的图象与 有两个公共点,则k的取值范围是 .
(1)、当 时,二次函数的对称轴为;(2)、 ;(3)、若二次函数的图象与 有两个公共点,则k的取值范围是 .三、解答题
-
20. 老师写出一个整式 (其中a、b为常数,且表示为系数),然后让同学给a、b赋予不同的数值进行计算,(1)、甲同学给出了一组数据,最后计算的结果为 ,则甲同学给出a、b的值分别是 , ;(2)、乙同学给出了 , ,请按照乙同学给出的数值化简整式;(3)、丙同学给出一组数,计算的最后结果与x的取值无关,请直接写出丙同学的计算结果.21. 观察下列两个等式: , ,给出定义如下:我们称使等式 成立的一对有理数“ , ”为“共生有理数对”,记为 ,如:数对 , 都是“共生有理数对”.(1)、通过计算判断数对“1,2”是不是“共生有理数对”;(2)、若 是“共生有理数对”,求a的值;(3)、若 是“共生有理数对”,则“ , ”“共生有理数对”(填“是”或“不是”);(4)、如果 是“共生有理数对”(其中 ),直接用含n的式子表示m.22. 某学校从甲、乙两位班主任中选拔一位参加局班主任技能大赛,选拔内容包括案例分析、班会设计、才艺展示三个项目,选拔比赛结束后,统计这两位班主任的成绩并制成了如图所示的条形统计图
 (1)、乙班主任三个项目的成绩的中位数是;(2)、用6张相同的卡片分别写上甲、乙两位班主任的六项成绩,洗匀后,从中任意抽取一张,求抽到的卡片写有“85”的概率;(3)、若按照如图所示的权重进行计算,选拔总分最高的一位班主任参加比赛,请你确定哪位班主任将获得参赛资格,说明理由23. 已知 的两边分别与⊙O相切于点A,B,⊙O的半径为r.
(1)、乙班主任三个项目的成绩的中位数是;(2)、用6张相同的卡片分别写上甲、乙两位班主任的六项成绩,洗匀后,从中任意抽取一张,求抽到的卡片写有“85”的概率;(3)、若按照如图所示的权重进行计算,选拔总分最高的一位班主任参加比赛,请你确定哪位班主任将获得参赛资格,说明理由23. 已知 的两边分别与⊙O相切于点A,B,⊙O的半径为r. (1)、如图1,点C在点A,B之间的优弧上, ,则 ;(2)、如图2,点C在圆上运动,当 最大时(即连接 并延长交⊙O于点C),连接 , ,
(1)、如图1,点C在点A,B之间的优弧上, ,则 ;(2)、如图2,点C在圆上运动,当 最大时(即连接 并延长交⊙O于点C),连接 , ,①求证: ;
②若 交⊙O于另一点D, ,求图中对应的阴影部分的周长(用含r的式子表示).
24. 如图,直角坐标系 中,过点 的直线 与直线 : 相交于点 ,直线 与x轴交于点B.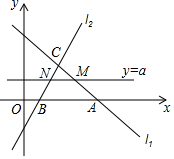 (1)、k的值为;(2)、求 的函数表达式和 的值;(3)、直线 与直线 和直线 分别交于点M,N,(M,N不同)
(1)、k的值为;(2)、求 的函数表达式和 的值;(3)、直线 与直线 和直线 分别交于点M,N,(M,N不同)①直接写出M,N都在y轴右侧时a的取值范围;
②在①的条件下,以 为边作正方形 ,边 恰好在x轴上,直接写出此时a的值.
25. 如图,C为 的边 上一点, ,N为边 上异于点O的一动点,P是线段 上一点,过点P分别作 交 于点Q, 交 于点M. (1)、若 , , ,求 的长;(提示:过点P作 )(2)、当点 在边 上运动时,四边形 始终保持为菱形,
(1)、若 , , ,求 的长;(提示:过点P作 )(2)、当点 在边 上运动时,四边形 始终保持为菱形,①证明: 是定值;
②设菱形 的面积为 , 的面积为 ,求 的取值范围.
26. 某公司生产一种产品,月销售量为x吨( ),每吨售价为7万元,每吨的成本y(万元)由两部分组成,一部分是原材料费用a固定不变,另一部分人力等费用, 与月销售量x成反比,市场部研究发现月销售量x吨与月份n(n为1~12的正整数)符合关系式 (k为常数),参考下面给出的数据解决问题.月份n(月)
1
2
成本y(万元/吨)
5
5.6
销售量为x(吨/月)
120
100
(1)、求 与x的函数关系式;(2)、求k的值;(3)、在这一年12个月中,①求月最大利润;
②若第m个月和第 个月的利润相差最大,直接写出m的值.