河北省保定市定兴县2021年中考数学一模试卷
试卷更新日期:2021-06-04 类型:中考模拟
一、单选题
-
1. 平方是 的数是( )A、 B、 C、 D、2. 如图,经过创平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( )
 A、两点确定一条直线 B、两点之间线段最短 C、垂线段最短 D、在同一平面内,过一点有且只有一条直线与已知直线垂直3. 华为 手机搭载了全球首款7纳米制程芯片,7纳米就是0.000000007米.数据0.000000007用科学记数法表示为( ).A、 B、 C、 D、4. 如图是由7个小正方体组合成的几何体,则其左视图为( )
A、两点确定一条直线 B、两点之间线段最短 C、垂线段最短 D、在同一平面内,过一点有且只有一条直线与已知直线垂直3. 华为 手机搭载了全球首款7纳米制程芯片,7纳米就是0.000000007米.数据0.000000007用科学记数法表示为( ).A、 B、 C、 D、4. 如图是由7个小正方体组合成的几何体,则其左视图为( )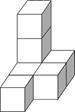 A、
A、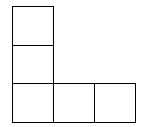 B、
B、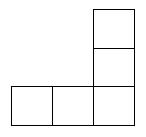 C、
C、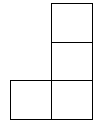 D、
D、 5. 下列四个数:3, , , 中,绝对值最大的数是A、3 B、 C、 D、6. 丽华根据演讲比赛中九位评委所给的分数作了如下表格
5. 下列四个数:3, , , 中,绝对值最大的数是A、3 B、 C、 D、6. 丽华根据演讲比赛中九位评委所给的分数作了如下表格平均数
中位数
众数
方差
8.5
8.3
8.1
0.15
如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
A、平均数 B、众数 C、方差 D、中位数7. 计算 的结果为( )A、 B、 C、 D、8. 化简 的结果为 ,则M为( )A、 B、 C、 D、9. 如图,证明矩形的对角线相等,已知:四边形 是矩形.求证: .以下是排乱了的证明过程:①∴ 、 .②∵ ③∵四边形 是矩形④∴ ⑤∴ .证明步骤正确的顺序是( ) A、③①②⑤④ B、②①③⑤④ C、③⑤②①④ D、②⑤①③④10. 如图,点 , ,以原点O为位似中心,把线段AB缩短为原来的一半,得到线段CD,其中点C与点A对应,点D与点B对应,则点D的横坐标为( )
A、③①②⑤④ B、②①③⑤④ C、③⑤②①④ D、②⑤①③④10. 如图,点 , ,以原点O为位似中心,把线段AB缩短为原来的一半,得到线段CD,其中点C与点A对应,点D与点B对应,则点D的横坐标为( )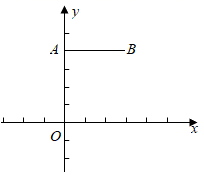 A、2 B、2或-2 C、 D、 或-11. 某中学八年级学生去距学校10千米的景点参观,一部分学生骑自行车先走,过了30分钟后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍.设骑车学生的速度为 千米/小时,则所列方程正确的是( )A、 B、 C、 D、12. 如图,在 中, ,以顶点A为圆心,适当长为半径画弧,分别交 , 于点M,N,再分别以点M,N为圆心,大于 长为半径画弧,两弧交于点P,作射线 交边 于点D,若 , ,则 的面积是( )
A、2 B、2或-2 C、 D、 或-11. 某中学八年级学生去距学校10千米的景点参观,一部分学生骑自行车先走,过了30分钟后,其余学生乘汽车出发,结果他们同时到达,已知汽车的速度是骑车学生速度的2倍.设骑车学生的速度为 千米/小时,则所列方程正确的是( )A、 B、 C、 D、12. 如图,在 中, ,以顶点A为圆心,适当长为半径画弧,分别交 , 于点M,N,再分别以点M,N为圆心,大于 长为半径画弧,两弧交于点P,作射线 交边 于点D,若 , ,则 的面积是( ) A、7 B、30 C、14 D、6013. 嘉嘉和淇淇玩一个游戏,他们同时从点B出发,嘉嘉沿正西方向行走,淇淇沿北偏东30°方向行走,一段时间后,嘉嘉恰好在淇淇的南偏西60°方向上.若嘉嘉行走的速度为1m/s,则淇淇行走的速度为( )
A、7 B、30 C、14 D、6013. 嘉嘉和淇淇玩一个游戏,他们同时从点B出发,嘉嘉沿正西方向行走,淇淇沿北偏东30°方向行走,一段时间后,嘉嘉恰好在淇淇的南偏西60°方向上.若嘉嘉行走的速度为1m/s,则淇淇行走的速度为( )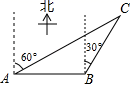 A、0.5 m/s B、0.8 m/s C、1 m/s D、1.2 m/s14. 二次函数 的图象如图所示,对称轴为直线 ,下列结论错误的是( )
A、0.5 m/s B、0.8 m/s C、1 m/s D、1.2 m/s14. 二次函数 的图象如图所示,对称轴为直线 ,下列结论错误的是( )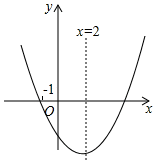 A、 B、当 时,顶点的坐标为 C、当 时, D、当 时,y随x的增大而增大15. 如图, 是 纸片的中位线,将 沿 所在的直线折叠,点 落在 边上的点 处,已知 的面积为7,则图中阴影部分的面积为( )
A、 B、当 时,顶点的坐标为 C、当 时, D、当 时,y随x的增大而增大15. 如图, 是 纸片的中位线,将 沿 所在的直线折叠,点 落在 边上的点 处,已知 的面积为7,则图中阴影部分的面积为( )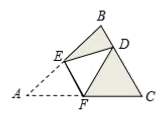 A、7 B、14 C、21 D、2816. 构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB , 连接AD , 得∠D=15°,所以tan15° .类比这种方法,计算tan22.5°的值为( )
A、7 B、14 C、21 D、2816. 构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB , 连接AD , 得∠D=15°,所以tan15° .类比这种方法,计算tan22.5°的值为( ) A、 B、 ﹣1 C、 D、
A、 B、 ﹣1 C、 D、二、填空题
-
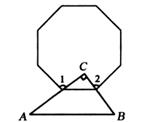
17. 计算: 的结果是 .18. 在图中,含30°的直角三角板的直角边AC,BC分别经过正八边形的两个顶点,则图中∠1+∠2= .
 19. 琪琪同学训练某种运算技能,每次训练完成相同数量的题目,各次训练题目难度相当.当训练次数不超过15次时,完成一次训练所需要的时间y(单位:秒)与训练次数x(单位:次)之间满足如图所示的反比例函数关系.完成第3次训练所需时间为400秒.
19. 琪琪同学训练某种运算技能,每次训练完成相同数量的题目,各次训练题目难度相当.当训练次数不超过15次时,完成一次训练所需要的时间y(单位:秒)与训练次数x(单位:次)之间满足如图所示的反比例函数关系.完成第3次训练所需时间为400秒.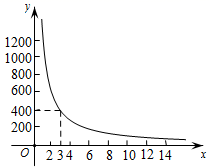 (1)、y与x之间的函数关系式为;x取值范围是 .(2)、当x的值为6,8,10时,对应的函数值分别为 ,比较 与 的大小: .
(1)、y与x之间的函数关系式为;x取值范围是 .(2)、当x的值为6,8,10时,对应的函数值分别为 ,比较 与 的大小: .三、解答题
-
20. 小丽同学准备化简:(3x2﹣6x﹣8)﹣(x2﹣2x□6),算式中“□”是“+,﹣,×,÷”中的某一种运算符号.(1)、如果“□”是“×”,请你化简:(3x2﹣6x﹣8)﹣(x2﹣2x×6);(2)、若x2﹣2x﹣3=0,求(3x2﹣6x﹣8)﹣(x2﹣2x﹣6)的值;(3)、当x=1时,(3x2﹣6x﹣8)﹣(x2﹣2x□6)的结果是﹣8,请你通过计算说明“□”所代表的运算符号.21. 在数学活动课上,李老师设计了一个游戏活动,四名同学分别代表一种运算,四名同学可以任意排列,每次排列代表一种运算顺序,剩余同学中,一名学生负责说一个数,其他同学负责运算,运算结果既对又快者获胜,可以得到一个奖品.
下面我们用四个卡片代表四名同学(如图):
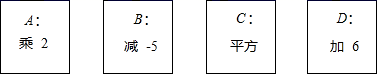 (1)、列式,并计算:
(1)、列式,并计算:①﹣3经过A,B,C,D的顺序运算后,结果是多少?
②5经过B,C,A,D的顺序运算后,结果是多少?
(2)、探究:数a经过D,C,A,B的顺序运算后,结果是45,a是多少?22. 如图, , ,直线 经过点D.设 ( ), 于点A,将射线 绕点C按逆时针方向旋转 ,与直线 交于点E.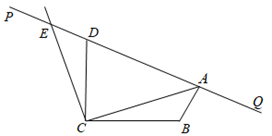
 (1)、判断: (填“ ”或“ ”或“ ”);(2)、猜想 的形状,并说明理由;(3)、若 的外心在其内部(不含边界),直接写出 的取值范围.23. 如图,在△ABC中,AB=AC,O是边AC上的点,以OC为半径的圆分别交边BC、AC于点D、E,过点D作DF⊥AB于点F.
(1)、判断: (填“ ”或“ ”或“ ”);(2)、猜想 的形状,并说明理由;(3)、若 的外心在其内部(不含边界),直接写出 的取值范围.23. 如图,在△ABC中,AB=AC,O是边AC上的点,以OC为半径的圆分别交边BC、AC于点D、E,过点D作DF⊥AB于点F. (1)、求证:直线DF是⊙O的切线;(2)、若OC=1,∠A=45°,求劣弧DE的长.24. 如图,在平面直角坐标系中,直线 与直线 相交于点P,并分别与x轴相交于点A、B.
(1)、求证:直线DF是⊙O的切线;(2)、若OC=1,∠A=45°,求劣弧DE的长.24. 如图,在平面直角坐标系中,直线 与直线 相交于点P,并分别与x轴相交于点A、B. (1)、求交点P的坐标;(2)、求 PAB的面积;(3)、请把图象中直线 在直线 上方的部分描黑加粗,并写出此时自变量x的取值范围.25. 某球室有三种品牌的 个乒乓球,价格是7,8,9(单位:元)三种.从中随机拿出一个球,已知 (一次拿到 元球) .(1)、求这 个球价格的众数;(2)、若甲组已拿走一个 元球训练,乙组准备从剩余 个球中随机拿一个训练.
(1)、求交点P的坐标;(2)、求 PAB的面积;(3)、请把图象中直线 在直线 上方的部分描黑加粗,并写出此时自变量x的取值范围.25. 某球室有三种品牌的 个乒乓球,价格是7,8,9(单位:元)三种.从中随机拿出一个球,已知 (一次拿到 元球) .(1)、求这 个球价格的众数;(2)、若甲组已拿走一个 元球训练,乙组准备从剩余 个球中随机拿一个训练.①所剩的 个球价格的中位数与原来 个球价格的中位数是否相同?并简要说明理由;
②乙组先随机拿出一个球后放回,之后又随机拿一个,用列表法(如图)求乙组两次都拿到8元球的概率.
又拿
先拿
 26. 某公司为了宣传一种新产品,在某地先后举行40场产品促销会,已知该产品每台成本为10万元,设第x场产品的销售量为y (台),在销售过程中获得以下信息:
26. 某公司为了宣传一种新产品,在某地先后举行40场产品促销会,已知该产品每台成本为10万元,设第x场产品的销售量为y (台),在销售过程中获得以下信息:信息1:已知第一场销售产品49台,然后每增加一场,产品就少卖出1台;
信息2:产品的每场销售单价p(万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场--第20场浮动价与销售场次x成正比,第21场--第40场浮动价与销售场次x成反比,经过统计,得到如下数据:
x(场)
3
10
25
p(万元)
10.6
12
14.2
(1)、求y与x之间满足的函数关系式;(2)、当产品销售单价为13万元时,求销售场次是第几场?(3)、在这40场产品促销会中,哪一场获得的利润最大,最大利润是多少?